初中数学华师大版八年级下册18.2 平行四边形的判定评课课件ppt

这是一份初中数学华师大版八年级下册18.2 平行四边形的判定评课课件ppt，共26页。PPT课件主要包含了学习目标，复习引入，导入新课，讲授新课，证一证，同理可证AD∥BC，归纳总结，∵AECF，又∵BODO，典例精析等内容，欢迎下载使用。

1.利用对角线互相平分判定平行四边形;（重点）
2.平行四边形对角线互相平分的相关运用;（难点）
3.利用两组对角相等判定平行四边形.（重点）
问题1 除了两组对边分别平行，平行四边形还有哪些性质？
平行四边形的对角相等.
平行四边形的对角线互相平分.
思考 我们得到的这些逆命题是否都成立？这节课我们一起探讨一下吧.
问题2 上面的两条条性质的逆命题各是什么？
两组对角分别相等的四边形是平行四边形；
对角线互相平分的四边形是平行四边形.
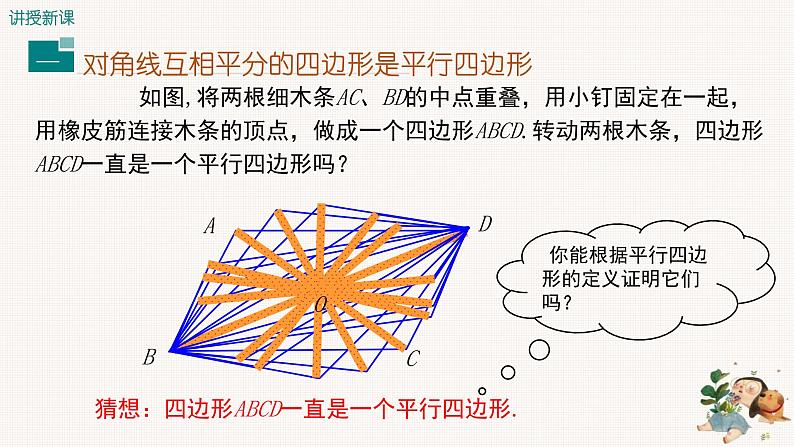
如图,将两根细木条AC、BD的中点重叠，用小钉固定在一起，用橡皮筋连接木条的顶点，做成一个四边形ABCD.转动两根木条，四边形ABCD一直是一个平行四边形吗？
猜想：四边形ABCD一直是一个平行四边形.
你能根据平行四边形的定义证明它们吗？
已知：四边形ABCD中，OA=OC，OB=OD.求证：四边 形ABCD是平行四边形.
在△AOB和△COD中,
OA=OC (已知)，
OB=OD (已知)，
∠AOB=∠COD (对顶角相等)，
∴△AOB≌△COD(SAS)，
∴ ∠BAO=∠OCD ,
∴AB∥ CD ,
∴四边形ABCD是平行四边形.
平行四边形的判定定理3：对角线互相平分的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AO=CO,DO=BO,∴四边形ABCD是平行四边形.
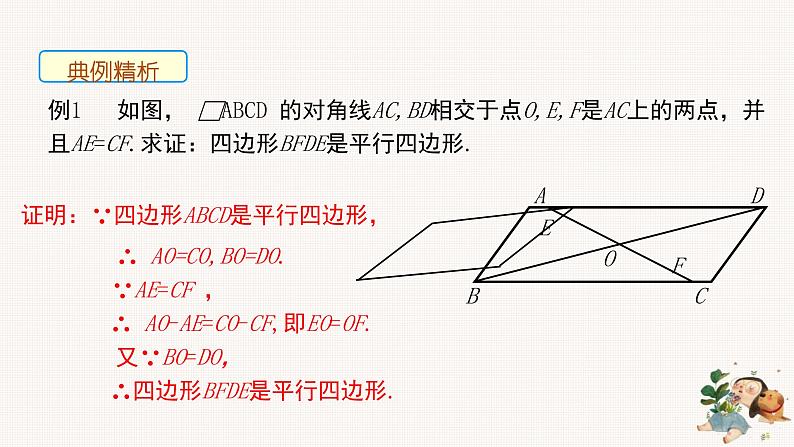
例1 如图， □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形，
∴ AO=CO,BO=DO.
∴ AO-AE=CO-CF,即EO=OF.
∴四边形BFDE是平行四边形.
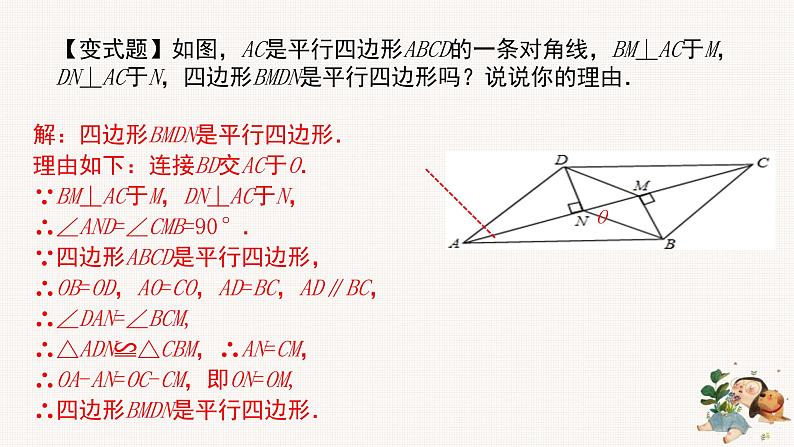
【变式题】如图，AC是平行四边形ABCD的一条对角线，BM⊥AC于M，DN⊥AC于N，四边形BMDN是平行四边形吗？说说你的理由．
解：四边形BMDN是平行四边形．理由如下：连接BD交AC于O．∵BM⊥AC于M，DN⊥AC于N，∴∠AND=∠CMB=90°．∵四边形ABCD是平行四边形，∴OB=OD，AO=CO，AD=BC，AD∥BC，∴∠DAN=∠BCM,∴△ADN≌△CBM，∴AN=CM，∴OA-AN=OC-CM，即ON=OM,∴四边形BMDN是平行四边形．
拓展探究 昨天李明同学在生物实验室做实验时，不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想回家去割一块赔给学校，带上玻璃剩下部分去玻璃店不安全，于是他想把原来的平行四边形重新在纸上画出来，然后带上图纸去就行了，可怎么画出原来的平行四边形呢(A,B,C为三顶点,即找出第四个顶点D)？
方法依据：两组对边分别平行的四边形是平行四边形.
方法依据：两组对边分别相等的四边形是平行四边形.
方法依据：对角线互相平分的四边形是平行四边形.
1.根据下列条件,不能判定四边形为平行四边形的是 ( )A.两组对边分别相等 B.两条对角线互相平分C.两条对角线相等 D.两组对边分别平行
2.如图，在四边形ABCD中，AC与BD交于点O.
如果AC=8cm,BD=10cm,那么当AO=_____cm,BO=_____cm时，四边形ABCD是平行四边形.
观看下面视频，对于两组对角分别相等的四边形的形状你的猜想是什么?
已知：四边形ABCD中，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形.
又∵∠A=∠C，∠B=∠D，
∵∠A+∠C+∠B+∠D=360°，
∴2∠A+2∠B=360°，
即∠A+∠B=180°，
同理得 AB∥ CD，
平行四边形的判定定理：两组对角分别相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵∠A=∠C，∠B=∠D,∴四边形ABCD是平行四边形.
例2 如图，四边形ABCD中，AB∥DC，∠B＝55°，∠1＝85°，∠2＝40°.(1)求∠D的度数；(2)求证：四边形ABCD是平行四边形．
(1)解：∵∠D＋∠2＋∠1＝180°，∴∠D＝180°－∠2－∠1＝55°；(2)证明：∵AB∥DC，∴∠2＝∠CAB，∴∠DAB＝∠1＋∠2＝125°.∵∠DCB＋∠DAB＋∠D＋∠B＝360°，∴∠DCB＝∠DAB＝125°.又∵∠D＝∠B＝55°，∴四边形ABCD是平行四边形．
1.判断下列四边形是否为平行四边形：
2.能判定四边形ABCD是平行四边形的条件： ∠A:∠B:∠C:∠D的值为 （　　）
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作，可是他不知道该怎样选，请同学们帮他选一选，哪四根木条可以制作成平行四边形木框，为什么？
发现：一组对边平行，另一组对边相等的四边形不一定是平行四边形.两组边相等的四边形也不一定是平行四边形.
想一想：判定一个四边形是平行边形可以从哪些角度思考?具体有哪些方法?
两组对边分别平行的四边形是平行四边形(定义法)
一组对边平行且相等的四边形是平行四边形(判定定理2)
两组对边分别相等的四边形是平行四边形（判定定理1）
两组对角分别相等的四边形是平行四边形（定义拓展）
对角线互相平分的四边形是平行四边形（判定定理3）
1.判断对错:(1)有一组对边平行的四边形是平行四边形. ( ) (2)有两条边相等，并且另外的两条边也相等的四边 形一定是平行四边形. ( )(3)对角线互相平分的四边形是平行四边形. ( ) (4)一条对角线平分另一条对角线的四边形是平行四 边形. ( )(5)有一组对角相等且一组对边平行的四边形是平行 四边形. ( )
2.如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（　　）A．OA=OC，OB=OD B．AB=CD，AO=CO C．AB=CD，AD=BC D．∠BAD=∠BCD，AB∥CD
3.如图，五边形ABCDE是正五边形，连接BD、CE，交于点P． 求证：四边形ABPE是平行四边形．
证明：∵五边形ABCDE是正五边形，∴正五边形的每个内角的度数是 AB=BC=CD=DE=AE，∴∠DEC=∠DCE= ×(180°-108°)=36°，同理∠CBD=∠CDB=36°，∴∠ABP=∠AEP=108°-36°=72°，∴∠BPE=360°-108°-72°-72°=108°=∠A，∴四边形ABPE是平行四边形．
4.如图，△ABC中，AB=AC=10，D是BC边上的任意一点，分别作DF∥AB交AC于F，DE∥AC交AB于E，求DE+DF的值．
解：∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∴DE=AF.又∵AB=AC=10，∴∠B=∠C.∵DF∥AB，∴∠CDF=∠B，∴∠CDF=∠C，∴DF=CF，∴DE+DF=AF+FC=AC=10．