初中数学人教版九年级上册24.1.1 圆复习ppt课件
展开1.圆的定义:到定点的距离等于定长的点的集合叫做圆.
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
弦、弧、圆心角、圆周角
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半.
直径所对的圆周角是直角. 90°的圆周角所对的弦是直径.
(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.
(2)圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,即圆具有旋转不变性.
1.如图,⊙O为△ABC的外接圆, AB为直径,AC=BC, 则∠A的 度数为 ;
2.⊙O中,弦AB所对的圆心角∠AOB=100°,则弦AB所对的圆周角为_________;
3.如何用一把直角尺检查镜上的装饰品是否恰好为半圆形?
4.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O与点F.(1)AB与AC的大小有什么关系?为什么?(2)按角的大小分类, 请你判断△ABC属于哪一类三角形,并说明理由。
重视:垂径定理——直角三角形
若 ① CD是直径
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
由 ① CD是直径
有关垂径定理的问题常涉及到半径、弦、弦心距、平行弦、弓形高
1、⊙O的半径为10,弦AB∥CD,AB=16,CD=12,则AB、CD间的距离是___.
2、如图,CD为⊙O直径,弦AB⊥CD于点E,CE=1,AB=10,则CD= .
3、如图,⊙M与x轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是 .
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
性质:(1)在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.
在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧相等.
∵∠ADB与∠AEB 、∠ACB 是同弧所对的圆周角
∴∠ADB=∠AEB =∠ACB
性质 3:半圆或直径所对的圆周角都相等,都等于900(直角).
性质4: 900的圆周角所对的弦是圆的直径.
不在同一直线上的三个点确定一个圆。
5. 已知:△ABC,AC=12,BC=5,AB=13,则△ABC的外接圆半径为 。
6. 如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标(4,4),则该圆弧所在圆的圆心坐标为 。
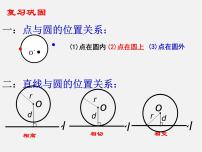
(1)当直线与圆相离时d>r;
(2)当直线与圆相切时d =r;
(3)当直线与圆相交时d<r.
直线与圆位置关系的识别:
设圆的半径为r,圆心到直线的距离为d,则:
经过半径的外端,并且垂直于这条半径的直线是圆的切线.
圆的切线垂直于过切点的半径.
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
1.与圆有一个公共点的直线。
2.圆心到直线的距离等于圆的半径的直线是圆的切线。
3.经过半径的外端且垂直于这条半径的直线是圆的切线。
∵OA是半径,OA⊥ l
∴直线l是⊙O的切线.
(1)圆的切线垂直于经过切点的半径.
(2)经过圆心垂直于切线的直线必经过切点.
(3)经过切点垂直于切线的直线必经过圆心.
∵直线l是⊙O的切线,切点为A
从圆外一点引圆的两条切线,它们的切线长相等;这点与圆心的连线平分这两条切线的夹角。
∵PA、PB为⊙O的切线
不在同一直线上的三点确定一个圆.
三角形的外接圆与内切圆:
三角形的外心就是三角形各边垂直平分线的交点.
三角形的内心就是三角形各角平分线的交点.
等边三角形的外心与内心重合.
内切圆半径与外接圆半径的比是1:2.
1.已知圆心O到直线a的距离为5,圆的半径为r,当r=__时,圆O与a相切.
2.如图圆O切PB于点B,PB=4,PA=2,则圆O的半径是____.
3.如图PA,PB,CD都是圆O的切线,PA的长为4cm,则△PCD的周长为_____cm
4.如图,PA、PB是圆的切线,A、B为切点,AC为直径,∠BAC=200,则∠P= 。
直角三角形的内切圆半径与三边关系:
三角形的内切圆半径与圆面积:
1.已知⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是 ;
2.已知两圆的半径分别是2和3,两圆的圆心距是4,则这两个圆的位置关系是 ;
3.两圆相切,圆心距为10cm,其中一个圆的半径为6cm,则另一个圆的半径为_____;
4. 已知圆O1与圆O 2的半径分别为12和2,圆心O1的坐标为(0,8),圆心O2 的坐标为(-6,0),则两圆的位置关系是______;
边长、半径、边心距中心角、内角
2.半径:正多边形外接圆的半径叫做这个正多边形的半径.
1.中心:一个正多边形外接圆的圆心叫做这个正多边形的中心.
3.中心角:正多边形每一边所对的外接圆的圆心角叫做这个正多边形的中心角.
4.边心距:中心到正多边形一边的距离叫做这个正多边形的边心距.
圆锥的侧面积和全面积:
1.扇形AOB的半径为12cm,∠AOB=120°求弧AB的长和扇形的面积及周长.
2.如图,当半径为30cm的转动轮转过120°时,传送带上的物体A平移的距离为____.
3.小红准备用纸板制作圆锥形的礼帽,圆锥帽底面积半径为9cm,母线长为36cm,请你计算制作一个这样的礼帽需要纸板的面积为_________.
如图,若AB,AC与⊙O相切与点B,C两点,P为弧 BC上任意一点,过点P作⊙O的切线交AB,AC于 点D,E,若AB=8,则△ADE的周长为_______;
①若∠A=70°,则∠BPC= ___ ;
②过点P作⊙O的切线MN,∠BPC=______________; (用∠A表示)
已知△ABC外切于⊙O,(1)若AB=8,BC=6,AC=4,则AD= __;BE= __;CF= __; (2)若C△ABC= 36, S△ABC=18,则r内=_____;
(3)若BE=3,CE=2, △ABC的周长为18,则AB=____;
AB+CD=AD+CB
(五)、相交两圆的连心线垂直平分公共弦
已知:⊙O1和⊙O2相交于A、B(如图)求证:O1O2是AB的垂直平分线
证明:连结O1A、O1B、O2A、O2B ∵ O1A=O1B ∴ O1点在AB的垂直平分线上 ∵ O2A=O2B ∴ O2点在AB的垂直平分线上 ∴ O1O2是AB的垂直平分线
9. ⊙O2和⊙O1相交于点A、B,它们的半径分别为2和 ,公共弦AB长为2,则(1)∠O1AO2=_____. (2)两圆的圆心距= .
(六)如图,设⊙O的半径为r,弦AB的长为a,弦 心距OD=d且OC⊥AB于D,弓形高CD为h,下面的说 法或等式: ①r=d+h, ②4r2=4d2+a2 ③已知:r、a、d、h中的任两个可求其他两个, 其中正确的结论的序号是( ) A.① B.①② C.①②③ D.②③
四、训练题:1.根据下列条件,能且只能作一个圆的是( ) A.经过点A且半径为R作圆; B.经过点A、B且半径为R作圆; C.经过△ABC的三个顶点作圆; D.过不在一条直线上的四点作圆;2.能在同一个圆上的是( ) A.平行四边形四个顶点; B.梯形四个顶点; C.矩形四边中点; D.菱形四边中点.
3.两圆的圆心都是点O,半径分别r1,r2,且 r1<OP<r2,那么点P在( ) A.⊙O内 B.小⊙O内 C. ⊙O外 D.小⊙O外,大⊙O内 4.下列说法正确的是( )A.三点确定一个圆; B.一个三角形只有一个外接圆;C.和半径垂直的直线是圆的切线;D.三角形的内心到三角形三个顶点距离相等.
5.与三角形三个顶点距离相等的点,是这个三角形的( ) A.三条中线的交点; B.三条角平分线的交点; C.三条高线的交点; D.三边中垂线的交点;6.圆的半径为5cm,圆心到一条直线的距离是7cm, 则直线与圆( ) A.有两个交点; B.有一个交点; C.没有交点; D.交点个数不定
7.若两圆的半径分别为R,r,圆心距为d,且满足R2+d2=r2+2Rd,则两圆的位置关系为( ) A.内切 B.内切或外切 C.外切 D.相交
由题意:R2+d2-2Rd=r2 即:(R-d)2 =r2∴ R-d = ±r ∴ R±r = d即两圆内切或外切
8.(苏州市)如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=( ) A.35° B.70° C.110° D.140°
9、(广州市)如图,A是半径为5的⊙O内的 一点,且OA=3,过点A且长小于8的 ( ) A.0条 B.1条 C.2条 D.4条
过点A且弦长为整数的弦有( )条
10、在等腰△ABC中,AB=AC=2cm,若以A为圆心,1cm为半径的圆与BC相切,则∠ABC的度数为 ( )A、30° B、60° C、90° D、120°
11、定圆0的半径是4cm,动圆P的半径是1cm,若⊙ P和⊙ 0相切,则符合条件的圆的圆心P构成的图形是 ( )
解:(1)若⊙0和⊙P外切,则OP=R+r =5cm ∴P点在以O为圆心,5cm为半径的圆上;
(2)若⊙0和⊙P内切,则OP=R-r=3cm∴P点在以O为圆心,3cm为半径的圆上。
解:设大圆半径R=3x,小圆半径r=2x 依题意得:3x-2x=8,解得:x=8 ∴ R=24 cm,r=16cm ∵ 两圆相交,∴R-r
13.△ABC中, ∠A=70°,⊙O截△ABC三条边所得的弦长相等.则 ∠BOC=°B.135°C.130°D.125°
14.梯形ABCD外切于⊙O,AD∥BC,AB=CD,
(1)若AD=4,BC=16,则⊙O的直径为_______;
(2)若AO=6,BO=8,则S⊙O=_______ ;
15、如图,AB是半⊙O的直径,AB=5,BC = 4, ∠ABC的角平分线交半圆于点D,AD,BC 的延长线相交于点E,则四边形ABCD的 面积是△DCE的面积的 ( ) A.9倍 B.8倍 C.7倍 D.6倍
16、如图,以O为圆心的两同心圆的半径分别是11cm和9cm,若⊙P与这两个圆都相切,则下列说法正确的有( )①⊙P的半径可以是2cm;②⊙P的半径可以是10cm;③符合条件的⊙P有无数个, 且点P的路线是曲线;④符合条件的⊙P有无数个, 且点P的路线是直线;A.1个 B.2个 C.3个 D.0个
17.如图Rt△ABC中,AB=10,BC=8,以点为圆心, 4.8为半径的圆与线段AB的位置关系 是___________;
当 ______________ 时,⊙O与线段AB没交点;当______________时,⊙O与线段AB有两个交点;当 ______________ 时,⊙O与线段AB仅有一交点;
r =4.8 或6<r≤8
1.如图, ⊙O的直径AB=12,以OA为直径的⊙O1交大圆的弦AC于D,过D点作小圆的切线交OC于点E,交AB于F.
(2)猜想DF与OC的位置关系,并说明理由.
(1)说明D是AC的中点.
(3)若DF=4,求OF的长.
数学人教版24.1.1 圆课文内容课件ppt: 这是一份数学人教版24.1.1 圆课文内容课件ppt,共16页。PPT课件主要包含了类比圆心角探知圆周角,圆周角和圆心角的关系,∵OAOB,∴∠A∠B,∴∠AOC2∠B,圆周角定理,解∵AB是直径,在Rt△ABC中,∵CD平分∠ACB,∴ADBD等内容,欢迎下载使用。
人教版九年级上册24.1.1 圆备课ppt课件: 这是一份人教版九年级上册24.1.1 圆备课ppt课件,共10页。PPT课件主要包含了∠AOB,∠COD,∠AOC,∠BOD,圆心角的概念,前提条件,ACBD,等式的性质,∠1∠245°,又∠ACB60°等内容,欢迎下载使用。
初中数学24.1.1 圆教课内容课件ppt: 这是一份初中数学24.1.1 圆教课内容课件ppt,共13页。PPT课件主要包含了几何符号表达,〖例1〗,〖例2〗,课堂小结,直线l,与圆有唯一公共点,l是圆的切线等内容,欢迎下载使用。