2018年北京市朝阳区中考一模数学试卷

这是一份2018年北京市朝阳区中考一模数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共8小题；共40分）
1. 如图，直线 a∥b，则直线 a，b 之间距离是
A. 线段 AB 的长度B. 线段 CD 的长度
C. 线段 EF 的长度D. 线段 GH 的长度

2. 若代数式 2xx−1 有意义，则实数 x 的取值范围是
A. x=0B. x=1C. x≠0D. x≠1

3. 若右图是某几何体的三视图，则这个几何体是
A. 球B. 圆柱C. 圆锥D. 三棱柱

4. 已知 l1∥l2，一个含有 30∘ 角的三角尺按照如图所示位置摆放，则 ∠1+∠2 的度数为
A. 90∘B. 120∘C. 150∘D. 180∘

5. 下列图形中，是中心对称图形，但不是轴对称图形的是
A. B.
C. D.

6. 实数 a，b，c，d 在数轴上的对应点的位置如图所示，下列结论① a＜b；② b=d；③ a+c=a；④ ad>0 中，正确的有
A. 4 个B. 3 个C. 2 个D. 1 个

7. “享受光影文化，感受城市魅力”，2018 年 4 月 15∼22 日第八届北京国际电影节顺利举办．下面的统计图反映了北京国际电影节．电影市场的有关情况．
根据统计图提供的信息，下列推断合理的是
A. 两届相比较，所占比例最稳定的是动作冒险（含战争）类
B. 两届相比较，所占比例增长最多的是剧情类
C. 第八届悬疑惊悚犯罪类申报数量比第六届 2 倍还多
D. 在第六届中，所占比例居前三位的类型是悬疑惊悚犯罪类、剧情类和爱情类

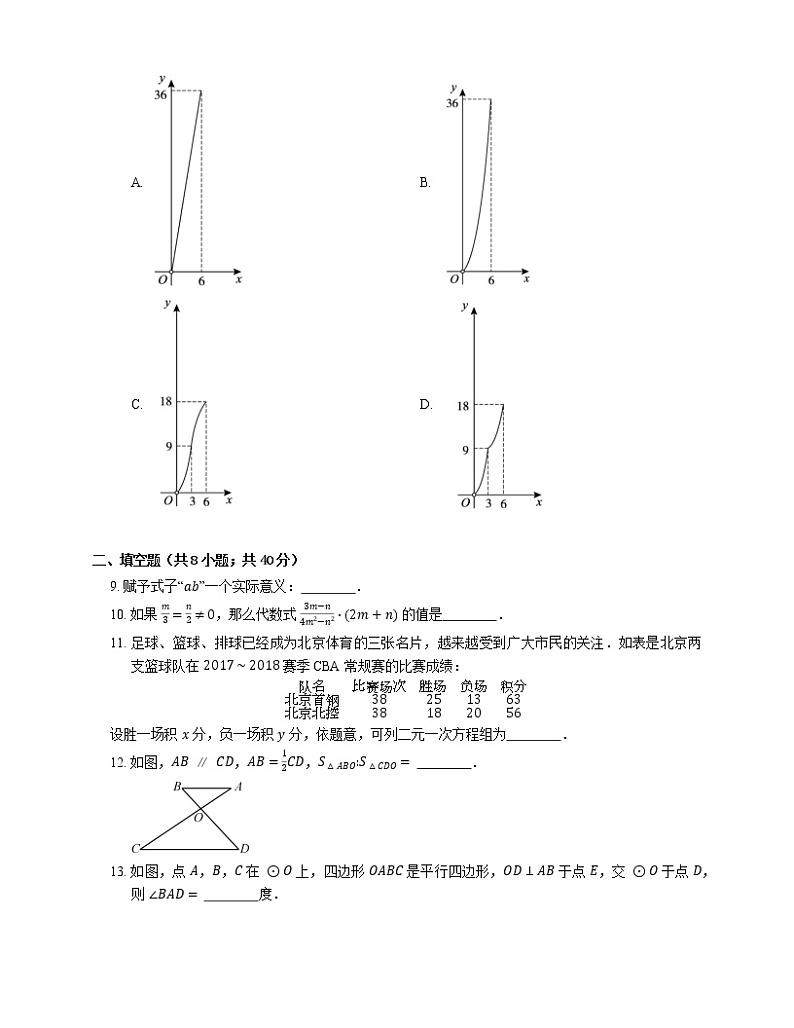
8. 如图，△ABC 是等腰直角三角形，∠A=90∘，AB=6，点 P 是 AB 边上一动点（点 P 与点 A 不重合），以 AP 为边作正方形 APDE，设 AP=x，正方形 APDE 与 △ABC 重合部分（阴影部分）的面积为 y，则下列能大致反映 y 与 x 的函数关系的图象是
A. B.
C. D.

二、填空题（共8小题；共40分）
9. 赋予式子“ab”一个实际意义： ．

10. 如果 m3=n2≠0，那么代数式 3m−n4m2−n2⋅2m+n 的值是 ．

11. 足球、篮球、排球已经成为北京体育的三张名片，越来越受到广大市民的关注．如表是北京两支篮球队在 2017∼2018 赛季CBA常规赛的比赛成绩：
队名比赛场次胜场负场积分北京首钢38251363北京北控38182056
设胜一场积 x 分，负一场积 y 分，依题意，可列二元一次方程组为 ．

12. 如图，AB∥CD，AB=12CD，S△ABO:S△CDO= ．

13. 如图，点 A，B，C 在 ⊙O 上，四边形 OABC 是平行四边形，OD⊥AB 于点 E，交 ⊙O 于点 D，则 ∠BAD= 度．

14. 如图，在平面直角坐标系 xOy 中，△OʹAʹBʹ 可以看作是 △OAB 经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由 △OAB 得到 △OʹAʹBʹ 的过程： ．

15. 下列随机事件的概率：①投掷一枚均匀的骰子，朝上一面为偶数的概率；②同时抛掷两枚质地均匀的硬币，两枚硬币全部正面朝上的概率；③抛一枚图钉，“钉尖向下”的概率；④某作物的种子在一定条件下的发芽率．既可以用列举法求得又可以用频率估计获得的是 （只填写序号）．

16. 下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程．
已知：直线 a 和直线外一点 P．
求作：直线 a 的垂线，使它经过 P．
作法：如图，
（1）在直线 a 上取一点 A，连接 PA；
（2）分别以点 A 和点 P 为圆心，大于 AP 的长为半径作弧，两弧相交于 B，C 两点，连接 BC 交 PA 于点 D；
（3）以点 D 为圆心，DP 为半径作圆，交直线 a 于点 E，作直线 PE．
∴ 直线 PE 就是所求作的垂线．
请回答：该尺规作图的依据是 ．

三、解答题（共12小题；共156分）
17. 计算：2sin30∘+13−1+4−π0+8．

18. 解：原不等式组为 x−1>2x−3,6x−12>2x.

19. 如图，在 △ACB 中，AC=BC，AD 为 △ACB 的高线，CE 为 △ACB 的中线．求证：∠DAB=∠ACE．

20. 已知关于 x 的一元二次方程 x2+k+1x+k=0．
（1）求证：方程总有两个实数根；
（2）若该方程有一个根是正数，求 k 的取值范围．

21. 如图，在 △ABC 中，D 是 AB 边上任意一点，E 是 BC 边中点，过点 C 作 AB 的平行线，交 DE 的延长线于点 F，连接 BF，CD．
（1）求证：四边形 CDBF 是平行四边形；
（2）若 ∠FDB=30∘，∠ABC=45∘，BC=42，求 DF 的长．

22. 如图，在平面直角坐标系 xOy 中，直线 AB 与 x 轴、 y 轴分别交于点 A，B，与反比例函数 y=kx 的图象在第四象限交于点 C，CD⊥x 轴于点 D，tan∠OAB=2，OA=2，OD=1．
（1）求该反比例函数的表达式；
（2）点 M 是这个反比例函数图象上的点，过点 M 作 MN⊥y 轴，垂足为点 N，连接 OM，AN，如果 S△ABN=2S△OMN，直接写出点 M 的坐标．

23. 如图，在 ⊙O 中，C，D 分别为半径 OB，弦 AB 的中点，连接 CD 并延长，交过点 A 的切线于点 E．
（1）求证：AE⊥CE．
（2）若 AE=2，sin∠ADE=13，求 ⊙O 半径的长．

24. 水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚．对于市场最为关注的产量和产量的稳定性，进行了抽样调查，过程如下，请补充完整．
收集数据：从甲、乙两个大棚各收集了 25 株秧苗上的小西红柿的个数：
甲
26324051447444637374815462413354433451636473645433
乙
27354655483647688248576675273657576658617138474671
（1）整理、描述数据：按如下分组整理、描述这两组样本数据．
（说明：45 个以下为产量不合格，45 个及以上为产量合格，其中 45∼65 个为产量良好，65∼85 个为产量优秀）
分析数据：两组样本数据的平均数、众数和方差如表所示：
大棚平均数众数方差甲53543047乙53573022
（2）得出结论：
a．估计乙大棚产量优秀的秧苗数为 株；
b．可以推断出 大棚的小西红柿秧苗品种更适应市场需求，理由为 ．（至少从两个不同的角度说明推断的合理性）

25. 如图，AB 是 ⊙O 的直径，AB=4 cm，C 为 AB 上一动点，过点 C 的直线交 ⊙O 于 D，E 两点，且 ∠ACD=60∘，DF⊥AB 于点 F，EG⊥AB 于点 G，当点 C 在 AB 上运动时，设 AF=x cm，DE=y cm（当 x 的值为 0 或 3 时，y 的值为 2），探究函数 y 随自变量 x 的变化而变化的规律．
（1）通过取点、画图、测量，得到了 x 与 y 的几组对应值，如下表：
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：点 F 与点 O 重合时，DE 长度约为 cm（结果保留一位小数）．

26. 在平面直角坐标系 xOy 中，抛物线 y=ax2−4ax−4a≠0 与 y 轴交于点 A，其对称轴与 x 轴交于点 B．
（1）求点 A，B 的坐标；
（2）若方程 ax2−4ax−4=0a≠0 有两个不相等的实数根，且两根都在 1，3 之间（包括 1，3），结合函数的图象，求 a 的取值范围．

27. 如图，在菱形 ABCD 中，∠DAB=60∘，点 E 为 AB 边上一动点（与点 A，B 不重合），连接 CE，将 ∠ACE 的两边所在射线 CE，CA 以点 C 为中心，顺时针旋转 120∘，分别交射线 AD 于点 F，G．
（1）依题意补全图形；
（2）若 ∠ACE=α，求 ∠AFC 的大小（用含 α 的式子表示）；
（3）用等式表示线段 AE，AF 与 CG 之间的数量关系，并证明．

28. 对于平面直角坐标系 xOy 中的点 P 和线段 AB，其中 At,0，Bt+2,0 两点，给出如下定义：若在线段 AB 上存在一点 Q，使得 P，Q 两点间的距离小于或等于 1，则称 P 为线段 AB 的伴随点．
（1）当 t=−3 时，
①在点 P11,1，P20,0，P3−2,−1 中，线段 AB 的伴随点是 ；
②在直线 y=2x+b 上存在线段 AB 的伴随点 M，N，且 MN=5，求 b 的取值范围；
（2）线段 AB 的中点关于点 2,0 的对称点是 C，将射线 CO 以点 C 为中心，顺时针旋转 30∘ 得到射线 l，若射线 l 上存在线段 AB 的伴随点，直接写出 t 的取值范围．
答案
第一部分
1. B
2. D
3. C
4. A
5. A
【解析】A、不是轴对称图形，是中心对称图形．故此选项正确；
B、是轴对称图形，也是中心对称图形．故此选项错误；
C、是轴对称图形，不是中心对称图形．故此选项错误；
D、是轴对称图形，不是中心对称图形．故此选项错误．
6. B
7. A
8. C
第二部分
9. 答案不惟一，如：边长分别为 a，b 的矩形面积
10. 74
11. 25x+13y=63,18x+20y=56
12. 1:4
13. 15
14. 答案不唯一，如：以 x 轴为对称轴，作 △OAB 的轴对称图形，再将得到三角形沿向右平移 4 个单位长度
15. ①②
16. 与一条线段两个端点距离相等的点，在这条线段的垂直平分线上；直径所对的圆周角是直角
第三部分
17. 原式=2×12+3+1+22=5+22.
18. 解不等式 ①，得
x12.∴
原不等式组的解集为 12