2019_2020学年宁波市北仑区八上期末数学试卷

展开

这是一份2019_2020学年宁波市北仑区八上期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 下列各组数不可能是一个三角形的边长的是
A. 1，2，3B. 4，4，4C. 6，6，8D. 7，8，9

2. 满足 −1A. B.
C. D.

3. 如图，△ABC 中，AB=AC，D 是 BC 中点，下列结论中不正确的是
A. ∠B=∠CB. AD⊥BC
C. AD 平分 ∠BACD. AB=2BD

4. 在圆周长计算公式 C=2πr 中，对半径不同的圆，变量有
A. C，rB. C，π，rC. C，πD. C，2π，r

5. 一次函数 y=3x+6 的图象经过
A. 第一、二、三象限B. 第二、三、四象限
C. 第一、二、四象限D. 第一、三、四象限

6. 已知正比例函数 y=kxk≠0 的图象经过点 1,−2，则这个正比例函数的解析式为
A. y=2xB. y=−2xC. y=12xD. y=−12x

7. 已知 △ABC 中，∠A=12∠B=13∠C，则它的三条边之比为
A. 1:1:2B. 1:3:2C. 1:2:3D. 1:4:1

8. 如果不等式组 x+7<3x−7,x>n 的解集是 x>7，则 n 的取值范围是
A. n=7B. n<7C. n≥7D. n≤7

9. 如图，在平面直角坐标系中，以 O 为圆心，适当长为半径画弧，交 x 轴于点 M，交 y 轴于点 N，再分别以点 M，N 为圆心，大于 12MN 的长为半径画弧，两弧在第二象限交于点 P．若点 P 的坐标为 2x,y+1，则 y 关于 x 的函数关系式为
A. y=xB. y=−2x−1C. y=2x−1D. y=1−2x

10. 一次长跑中，当小明跑了 1600 米时，小刚跑了 1400 米，小明、小刚在此后所跑的路程 y（米）与时间 t（秒）之间的函数关系如图，则这次长跑的全程为
A. 2000 米B. 2100 米C. 2200 米D. 2400 米

二、填空题（共8小题；共40分）
11. 请用不等式表示“x 的 2 倍与 3 的和大于 1”：．

12. 已知 y 是 x 的正比例函数，当 x=−2 时，y=4，当 x=3 时，y= ．

13. 已知点 A 的坐标为 −2,3，则点 A 关于 x 轴的对称点 A1 的坐标是．

14. 如图，点 B，F，C，E 在同一直线上，BF=CE，AB∥DE，请添加一个条件，使 △ABC≌△DEF，这个添加的条件可以是（只需写一个，不添加辅助线）．

15. 命题“等腰三角形的两个底角相等”的逆命题是．

16. 在平面直角坐标系中，若点 Am,2 向上平移 3 个单位，向左平移 2 个单位后得到点 B3,n，则 m+n= ．

17. 如图，△ABC 中，∠ACB=90∘，D 在 BC 上，E 为 AB 之中点，AD，CE 相交于 F，且 AD=DB．若 ∠B=20∘，则 ∠DFE 等于 ∘．

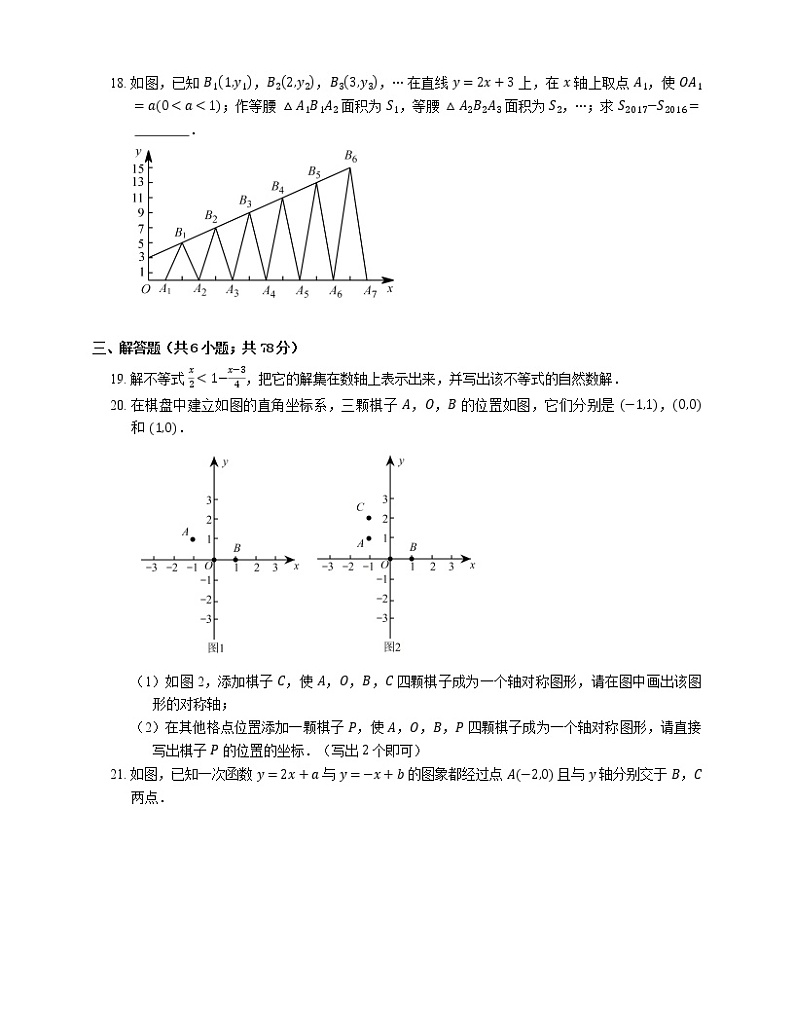
18. 如图，已知 B11,y1，B22,y2，B33,y3，⋯ 在直线 y=2x+3 上，在 x 轴上取点 A1，使 OA1=a0
三、解答题（共6小题；共78分）
19. 解不等式 x2<1−x−34，把它的解集在数轴上表示出来，并写出该不等式的自然数解．

20. 在棋盘中建立如图的直角坐标系，三颗棋子 A，O，B 的位置如图，它们分别是 −1,1，0,0 和 1,0．
（1）如图 2，添加棋子 C，使 A，O，B，C 四颗棋子成为一个轴对称图形，请在图中画出该图形的对称轴；
（2）在其他格点位置添加一颗棋子 P，使 A，O，B，P 四颗棋子成为一个轴对称图形，请直接写出棋子 P 的位置的坐标．（写出 2 个即可）

21. 如图，已知一次函数 y=2x+a 与 y=−x+b 的图象都经过点 A−2,0 且与 y 轴分别交于 B，C 两点．
（1）分别求出这两个一次函数的解析式；
（2）求 △ABC 的面积．

22. 某校八年级举行英语演讲比赛，购买A，B两种笔记本作为奖品．这两种笔记本的单价分别是 12 元和 8 元，根据比赛设奖情况需购买这两种笔记本共 30 本，并且所购买的A种笔记本的数量多于B种笔记本的数量，但又不多于B种笔记本数量 2 倍，如果设他们买A种笔记本 n 本，买这两种笔记本共花费 w 元．
（1）请写出 w（元）关于 n（本）的函数关系式，并求出自变量 n 的取值范围；
（2）请你帮助他们计算购买这两种笔记本各多少时，花费最少，此时的花费是多少元．

23. 在直线上顺次取 A，B，C 三点，分别以 AB，BC 为边长在直线的同侧作正三角形，作得两个正三角形的另一顶点分别为 D，E．
（1）如图①，连接 CD，AE，求证：CD=AE；
（2）如图②，若 AB=1，BC=2，求证：∠BDE=90∘；
（3）如图③，将图②中的正三角形 BEC 绕 B 点作适当的旋转，连接 AE，若有 DE2+BE2=AE2，试求 ∠DEB 的度数．

24. 如图，直线 y=kx−3 与 x 轴、 y 轴分别交于 B，C 两点，且 OC=2OB．
（1）求点 B 坐标和 k 值；
（2）若点 Ax,y 是直线 y=kx−3 上在第一象限内的一个动点，点 A 在运动过程中，求 △AOB 的面积 S 与 x 的函数关系式（不要求写自变量范围）；并进一步求出点 A 的坐标为多少时，△AOB 的面积为 94；
（3）在上述条件下，x 轴正半轴上是否存在点 P，使 △ABP 为等腰三角形?若存在请写出满足条件的所有 P 点坐标；若不存在，请说明理由．
答案
第一部分
1. A【解析】A．1+2=3，不能构成三角形；
B．4+4>4，能构成三角形；
C．6+6>8，能构成三角形；
D．7+8>9，能构成三角形．
2. B【解析】由于 x>−1，
∴ 表示 −1 的点应该是空心点，折线的方向应该是向右．
由于 x≤2，
∴ 表示 2 的点应该是实心点，折线的方向应该是向左．
∴ 数轴表示的解集为
3. D
4. A【解析】∵ 在圆的周长公式 C=2πr 中，C 与 r 是改变的，π 是不变的；
∴ 变量是 C，r，常量是 2π．
5. A
【解析】∵ 在一次函数 y=3x+6 中：k=3>0，b=6>0，
∴ 一次函数 y=3x+6 的图象经过第一、二、三象限．
6. B
7. B【解析】设 ∠C=6x∘，则 ∠A=2x∘，∠B=4x∘ .
∴12x=180 .
∴∠C=90∘，∠A=30∘，∠B=60∘ .
8. D【解析】x+7<3x−7, ⋯⋯①x>n, ⋯⋯②
解 ① 得 x>7，
解 ② 得 x>n，
而不等式组的解集是 x>7，
∴n≤7．
9. B
10. C
【解析】设小明的速度为 a 米/秒，小刚的速度为 b 米/秒，
由题意，得 1600+100a=1400+100b,1600+300a=1400+200b,
解得：a=2,b=4.
故这次越野跑的全程为：1600+300×2=2200（米）．
第二部分
11. 2x+3>1
【解析】由题意得，2x+3>1．
12. −6
【解析】设 y 与 x 之间的函数关系式是 y=kx，
把 x=−2，y=4 代入得：4=−2k，
解得：k=−2，
∴y=−2x，
当 x=3 时，y=−2×3=−6．
13. −2,−3
【解析】∵ 点 A 的坐标为 −2,3，
则点 A 关于 x 轴的对称点 A1 的坐标是 −2,−3．
14. AB=DE（答案不唯一）
【解析】∵BF=CE，
∴BF+FC=CE+FC，
∴BC=EF，
∵AB∥DE，
∴∠ABC=∠DEF，
在 △ABC 和 △DEF 中，
AB=DE,∠ABC=∠DEF,BC=EF,
∴△ABC≌△DEF．
15. 两个角相等三角形是等腰三角形
16. 10
【解析】∵ 点 Am,2 向上平移 3 个单位，向左平移 2 个单位后得到点 B3,n，
∴m−2=3，2+3=n，
∴m=5，n=5，
∴m+n=10．
17. 60
【解析】由直角三角形性质知，
∵E 为 AB 之中点，
∴CE=AE=BE（直角三角形斜边上的中线等于斜边的一半），
∴∠B=∠BCE=20∘，∠EAC=∠ECA=70∘，
∴∠ACF=70∘，
又 ∵AD=DB，
∴∠B=∠BAD=20∘，
∴∠FAC=50∘，
∴ 在 △ACF 中，
∠AFC=180∘−70∘−50∘=60∘，
∴∠DFE=∠AFC=60∘．
18. 4037−8072a
【解析】∵B11,y1，B22,y2，B33,y3，⋯ 在直线 y=2x+3 上，
∴y1=2×1+3=5，y2=2×2+3=7，y3=2×3+3=9，y4=2×4+3=11，⋯，yn=2n+3；
又 ∵OA1=a0 ∴S1=12×2×1−a×5=51−a；
S2=12×2×2−a−2×1−a×7=7a；
S3=12×2×3−a−2×1−a−2×2−a−2×1−a×9=91−a；
S4=12×2×1−1−a×11=11a；
⋯
∴Sn=2n+31−a（n 是奇数）；Sn=2n+3a（n 是偶数），
∴S2017−S2016=2×2017+31−a−2×2016+3a=4037−8072a．
第三部分
19. 去分母得：
2x<4−x−3.
去括号得：
2x<4−x+3.2x+x<4+3.3x<7.x<73.
在数轴上表示为：
不等式的自然数解为 0，1，2．
20. （1）如图3所示，
C 点的位置为 −1,2，A，O，B，C 四颗棋子组成等腰梯形，直线 l 为该图形的对称轴．
（2）如图 4 所示：
P0,−1，Pʹ−1,−1 都符合题意．
21. （1）把 A−2,0 分别代入 y=2x+a 和 y=−x+b 得，a=4，b=−2，
∴ 这两个函数分别为 y=2x+4 和 y=−x−2．
（2）在 y=2x+4 和 y=−x−2 中，
令 x=0，可分别求得 y=4 和 y=−2，
∴B0,4，C0,−2，
又 ∵A−2,0，
∴OA=2，BC=6，
∴S△ABC=12OA⋅BC=12×2×6=6．
22. （1）由题意可得，
w=12n+830−n=4n+240.
因为
n>30−n,n≤230−n,
解得，
15即 w（元）关于 n（本）的函数关系式是 w=4n+24015 （2）因为 w=4n+24015所以 n=16 时，w 取得最小值，此时 w=4×16+240=304，
所以 30−n=30−16=14，
即购买A种笔记本 16 本，B种笔记本 14 本时，花费最少，此时的花费是 304 元．
23. （1） ∵△ABD 和 △ECB 都是等边三角形，
∴AD=AB=BD，BC=BE=EC，∠ABD=∠EBC=60∘，
∴∠ABE=∠DBC，
在 △ABE 和 △DBC 中，
AB=BD,∠ABE=∠DBC,BE=BC,
∴△ABE≌△DBC，
∴CD=AE．
（2）如图②中，取 BE 中点 F，连接 DF．
∵BD=AB=1，BE=BC=2，∠ABD=∠EBC=60∘，
∴BF=EF=BD=1，∠DBF=60∘，
∴△DBF 是等边三角形，
∴DF=BF=EF，∠DFB=60∘，
∵∠BFD=∠FED+∠FDE，
∴∠FDE=∠FED=30∘，
∴∠EDB=180∘−∠DBE−∠DEB=90∘．
（3）如图③中，连接 DC，
∵△ABD 和 △ECB 都是等边三角形，
∴AD=AB=BD，BC=BE=EC，∠ABD=∠EBC=60∘，
∴∠ABE=∠DBC，
在 △ABE 和 △DBC 中，
AB=BD,∠ABE=∠DBC,BE=BC,
∴△ABE≌△DBC，
∴AE=DC．
∵DE2+BE2=AE2，BE=CE，
∴DE2+CE2=CD2，
∴∠DEC=90∘，
∵∠BEC=60∘，
∴∠DEB=∠DEC−∠BEC=30∘．
24. （1）在 y=kx−3 中，令 x=0，则 y=−3，
∴C 的坐标是 0,−3，
∴OC=3，
∵OC=2OB，
∴OB=12OC=32，则 B 的坐标是：32,0；
把 B 的坐标代入 y=kx−3，得：32k−3=0，
∴k=2．
（2） OB=32，则 S=12×322x−3=32x−94；
∵△AOB 的面积为 94；
∴32x−94=94，
∴x=3，则 A 的坐标是 3,3．
（3）设 Pm,0m>0，
由（1）（2）知，A3,3，B32,0，
∴AB2=3−322+9=454，AP2=m−32+9=m2−6m+18，BP2=m−322，
∵△ABP 为等腰三角形，
①当 AB=AP 时，
∴AB2=AP2，
∴454=m2−6m+18，
∴m=32（舍）或 m=92，
∴P92,0；
②当 AB=BP 时，
∴AB2=BP2，
∴454=m−322，
∴m=3−352（舍）或 m=3+352，
∴P3+352,0；
③当 AP=BP 时，AP2=BP2，
∴m2−6m+18=m−322，
∴m=214，
∴P214,0．
满足条件的 P 的坐标为 92,0 或 214,0 或 3+352,0．

2019_2020学年宁波市北仑区八上期末数学试卷

更专业

更丰富

更便捷

真低价

欢迎来到教习网