2019_2020学年福州市九上期末数学试卷

这是一份2019_2020学年福州市九上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

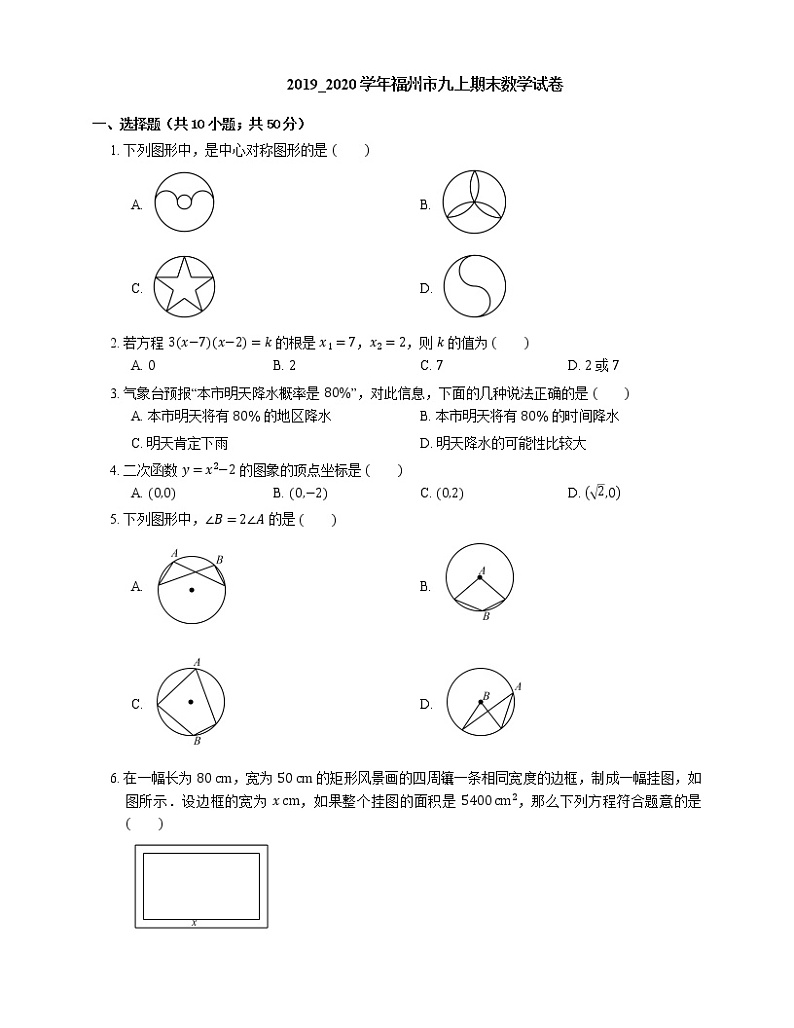
一、选择题（共10小题；共50分）
1. 下列图形中，是中心对称图形的是
A. B.
C. D.

2. 若方程 3x−7x−2=k 的根是 x1=7，x2=2，则 k 的值为
A. 0B. 2C. 7D. 2 或 7

3. 气象台预报“本市明天降水概率是 80%”，对此信息，下面的几种说法正确的是
A. 本市明天将有 80% 的地区降水B. 本市明天将有 80% 的时间降水
C. 明天肯定下雨D. 明天降水的可能性比较大

4. 二次函数 y=x2−2 的图象的顶点坐标是
A. 0,0B. 0,−2C. 0,2D. 2,0

5. 下列图形中，∠B=2∠A 的是
A. B.
C. D.

6. 在一幅长为 80 cm，宽为 50 cm 的矩形风景画的四周镶一条相同宽度的边框，制成一幅挂图，如图所示．设边框的宽为 x cm，如果整个挂图的面积是 5400 cm2，那么下列方程符合题意的是
A. 50−x80−x=5400B. 50−2x80−2x=5400
C. 50+x80+x=5400D. 50+2x80+2x=5400

7. 正六边形的两条对边之间的距离是 23，则它的边长是
A. 1B. 2C. 3D. 23

8. 若点 Mm,nmn≠0 在二次函数 y=ax2a≠0 的图象上，则下列坐标表示的点也在该抛物线上的是
A. −m,nB. n,mC. m2,n2D. m,−n

9. 在 ⊙O 中，将圆心绕着圆周上一点 A 旋转一定角度 θ，使旋转后的圆心落在 ⊙O 上，则 θ 的值可以是
A. 30∘B. 45∘C. 60∘D. 90∘

10. 圆心角为 60∘ 的扇形面积为 S，半径为 r，则下列图象能大致描述 S 与 r 的函数关系的是
A. B.
C. D.

二、填空题（共6小题；共30分）
11. 点 0,1 关于原点 O 对称的点是 ．

12. 从实数 −1，−2，1 中随机选取两个数，积为负数的概率是 ．

13. 已知 ∠APB=90∘，以 AB 为直径作 ⊙O，则点 P 与 ⊙O 的位置关系是 ．

14. 如图，利用标杆 BE 测量建筑物的高度．若标杆 BE 的高为 1.2 m，测得 AB=1.6 m，BC=12.4 m，则楼高 CD 为 m．

15. 已知平行四边形 ABCD 的面积为 4，对角线 AC 在 y 轴上，点 D 在第一象限内，且 AD∥x 轴，当双曲线 y=kx 经过 B，D 两点时，则 k= ．

16. 二次函数 y=x−2m2+m2，当 m
三、解答题（共9小题；共117分）
17. 解方程 x2+6x+1=0．

18. 已知关于 x 的一元二次方程 x−12=14m−1 有两个不相等的实数根，求 m 的取值范围．

19. 如图，△ABC 中，∠C=90∘，CA=CB=1，将 △ABC 绕点 B 顺时针旋转 45∘，得到 △DBE（A，D 两点为对应点），画出旋转后的图形，并求出线段 AE 的长．

20. 一个不透明的盒子中有 2 枚黑棋，x 枚白棋，这些棋子除颜色外无其他差别，现从盒中随机摸出一枚棋子（不放回），再随机摸出一枚棋子．
（1）若“摸出两枚棋子的颜色都是白色”是不可能事件，请写出符合条件的一个 x 值 ；
（2）当 x=2 时，“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由．

21. 如图，△ABC 中，点 D 在 BC 边上，有下列三个关系式：
① ∠BAC=90∘，② BDAD=ADDC，③ AD⊥BC．选择其中两个式子作为已知，余下的一个作为结论，写出已知，求证，并证明．
已知：
求证：
证明：

22. 如图，在左边托盘A（固定）中放置一个重物，在右边托盘B（可左右移动）中放置一定质量的砝码，可使得仪器左右平衡，改变托盘B与支撑点 M 的距离，记录相应的托盘B中的砝码质量，得到下表：
托盘B与点M的距离xcm1015202530托盘B中的砝码质量yg3020151210
（1）把上表中 x,y 的各组对应值作为点的坐标，在如图所示的平面直角坐标系中描出其余的点，并用一条光滑曲线连接起来；观察所画的图象，猜测 y 与 x 之间的函数关系，求出该函数解析式；
（2）当托盘B向左移动（不超过点 M）时，应往托盘B中添加砝码还是减少砝码?

23. 如图，在 Rt△ABC 中，∠C=90∘，O 为 AB 边上一点，⊙O 交 AB 于 E，F 两点，BC 切 ⊙O 于点 D，且 CD=12EF=1．
（1）求证：⊙O 与 AC 相切；
（2）求图中阴影部分的面积．

24. 在平面直角坐标系 xOy 中，对于点 Px,y，若点 Q 的坐标为 x,∣x−y∣，则称点 Q 为点 P 的“关联点”．
（1）请直接写出点 2,2 的“关联点”的坐标；
（2）如果点 P 在函数 y=x−1 的图象上，其“关联点”Q 与点 P 重合，求点 P 的坐标；
（3）如果点 Mm,n 的“关联点”N 在函数 y=x2 的图象上，当 0≤m≤2 时，求线段 MN 的最大值．

25. 如图，C 为线段 AB 上一点，分别以 AC，BC 为边在 AB 的同侧作等边 △HAC 与等边 △DCB，连接 DH．
（1）如图 1，当 ∠DHC=90∘ 时，求 BCAC 的值；
（2）在（1）的条件下，作点 C 关于直线 DH 的对称点 E，连接 AE，BE，求证：CE 平分 ∠AEB；
（3）现将图 1 中 △DCB 绕点 C 顺时针旋转一定角度 α0∘<α<90∘，如图 2，点 C 关于直线 DH 的对称点为 E，则（2）中的结论是否成立?给出证明．
答案
第一部分
1. D
2. A
3. D
4. B
5. D
6. D
7. B
8. A
9. C
10. A
第二部分
11. 0,−1
12. 23
13. 点 P 在 ⊙O 上
14. 10.5
【解析】因为 EB∥CD，
所以 △ABE∽△ACD，
所以 BECD=ABAC，
所以 1.2CD=1.61.6+12.4，
所以 CD=10.5 m．
15. 2
16. m≥1
第三部分
17.
∵x2+6x=−1,∴x2+6x+9=−1+9.
即
x+32=8,∴x+3=±22.
则
x=−3±22,x1=−3+22,x2=−3−22.
18. ∵ 方程 x−12=14m−1 有两个不相等的实数根，
∴14m−1>0，解得：m>4．
∴m 的取值范围为 m>4．
19. 如图，
∵∠C=90∘，CA=CB=1，
∴∠ABC=45∘，AB=2BC=2，
∵△ABC 绕点 B 顺时针旋转 45∘，得到 △DBE，
∴∠CBE=45∘，BC=BE=1，
∵∠CBE=∠CBA，
∴ 点 E 在 AB 上，
∴AE=AB−BE=2−1．
20. （1） 1（或 0）
【解析】若“摸出两枚棋子的颜色都是白色”是不可能事件，则 x 为 1 或 0．
（2） 不相等．理由如下：
画树状图为：
共有 12 种等可能的结果，其中摸出两枚棋子的颜色相同的结果数为 4，摸出两枚棋子的颜色不同的结果数为 8，
所以摸出两枚棋子的颜色相同的概率 =412=13，摸出两枚棋子的颜色不同的概率 =812=23，
所以“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率不相等．
21. 已知：①③，
求证：②，
证明：∵ AD⊥BC，
∴ ∠ADB=∠ADC=90∘，
∴ ∠BAD+∠B=90∘，
∵ ∠BAC=90∘，
∴ ∠B+∠C=90∘，
∴ ∠BAD=∠C，
∴ △ABD∽△CAD，
∴ BDAD=ADCD．
22. （1） 函数图象如图所示，
观察图象可知，函数可能是反比例函数，设 y=kxk≠0，
把 10,30 的坐标代入，得 k=300，
所以 y=300x，
经检验，其余各个点坐标均满足 y=300x．
所以该函数的解析式为 y=300x．
（2） 当托盘B向左移动（不超过点 M）时，应往托盘B中添加砝码．
由图象可知，当 x>0 时，y 随 x 的增大而减少，所以当托盘B向左移动时，x 减小，y 增大．
23. （1） 连接 OD，过点 O 作 OH⊥AC 于点 H，如图，
∵BC 是 ⊙O 的切线，
∴OD⊥BC．
∵∠C=90∘，
∴∠OHC=∠ODC=∠C=90∘，
∴ 四边形 OHCD 是矩形．
∵CD=12EF，
∴OH=12EF=OE．
∵OH⊥AC，
∴AC 是 ⊙O 的切线．
（2） ∵OD=12EF=1，CD=1，∠DOH=90∘，
∴S阴影=1×1−90π×12360=1−14π．
24. （1） ∵∣2−2∣=0，
∴ 点 2,2 的“关联点”的坐标为 2,0．
（2） ∵ 点 P 在函数 y=x−1 的图象上，
∴Px,x−1，则点 Q 的坐标为 x,1，
∵ 点 Q 与点 P 重合，
∴x−1=1，解得：x=2，
∴ 点 P 的坐标为 2,1．
（3） ∵ 点 Mm,n，
∴ 点 Nm,∣m−n∣．
∵ 点 N 在函数 y=x2 的图象上，
∴∣m−n∣=m2．
（i）当 m≥n 时，m−n=m2，
∴n=−m2+m，
∴Mm,−m2+m，Nm,m2．
∵0≤m≤2，
∴MN=∣yM−yN∣=∣−m2+m−m2∣=m∣2m−1∣．
① 当 0≤m≤12 时，MN=−2m2+m=−2m−142+18，
∴ 当 m=14 时，MN 取最大值，最大值为 18．
② 当 12当 m=2 时，MN 取最大值，最大值为 6．
（ii）当 m ∴ n=m2+m，
∴ Mm,m2+m，Nm,m2．
∵ 0≤m≤2，
∴ MN=∣yM−yN∣=∣m2+m−m2∣=m，
当 m=2 时，MN 取最大值 2．
综上所述，线段 MN 的最大值为 6．
25. （1） 因为 △HAC 与 △DCB 都是等边三角形，
所以 ∠ACH=∠DCB=60∘，AC=HC，BC=CD，
所以 ∠HCD=180∘−∠ACH−∠DCB=60∘，
因为 ∠DHC=90∘，
所以 ∠HDC=180∘−∠DHC−∠HCD=30∘，
所以 CD=2CH，
所以 BC=2AC，
所以 BCAC=2．
（2） 如图 1，
由对称性得 ∠EHD=90∘，EH=HC，
因为 AH=HC，
所以 EH=AH，
因为 ∠DHC=90∘，
所以 E，H，C 三点共线，
所以 ∠AEC=12∠AHC=30∘，
由（1）可得 BC=2CH=EC，
所以 ∠BEC=12∠ACE=30∘，
所以 ∠AEC=∠BEC，即 CE 平分 ∠AEB．
（3） 结论仍然正确，理由如下：
如图 2，
由对称性可知：HC=HE，
又因为 AH=HC，
所以 HC=HA=HE，
因为 A，C，E 三点都在以点 H 为圆心，HA 为半径的圆上，
所以 ∠AEC=12∠AHC=30∘，
同理可得，∠BEC=12∠BDC=30∘，
所以 ∠AEC=∠BEC，
所以 EC 平分 ∠AEB．