2019_2020学年苏州市石牌中学八上期末数学复习试卷（2）

这是一份2019_2020学年苏州市石牌中学八上期末数学复习试卷（2），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题；共50分）
1. 函数 y=3−x+1x−4 的自变量 x 的取值范围是
A. x≤3B. x≠4
C. x≥3 且 x≠4D. x≤3 或 x≠4

2. 如图，已知 AD 是 △ABC 的 BC 边上的高，下列能使 △ABD≌△ACD 的条件是
A. AB=ACB. ∠BAC=90∘C. BD=ACD. ∠B=45∘

3. 实数 a，b 在数轴上的位置如图所示，且 ∣a∣>∣b∣，则化简 a2−∣a+b∣ 的结果为
A. 2a+bB. −2a+bC. bD. 2a−b

4. 用四舍五入法按要求对 0.05049 分别取近似值，其中错误的是
A. 0.1（精确到 0.1）B. 0.05（精确到百分位）
C. 0.05（精确到千分位）D. 0.050（精确到 0.001）

5. 下列各式化简结果为无理数的是
A. 3−27B. 2−10C. 8D. −22

6. 如图，在 △ABC 中，AC=4 cm，线段 AB 的垂直平分线交 AC 于点 N，△BCN 的周长是 7 cm，则 BC 的长为
A. 1 cmB. 2 cmC. 3 cmD. 4 cm

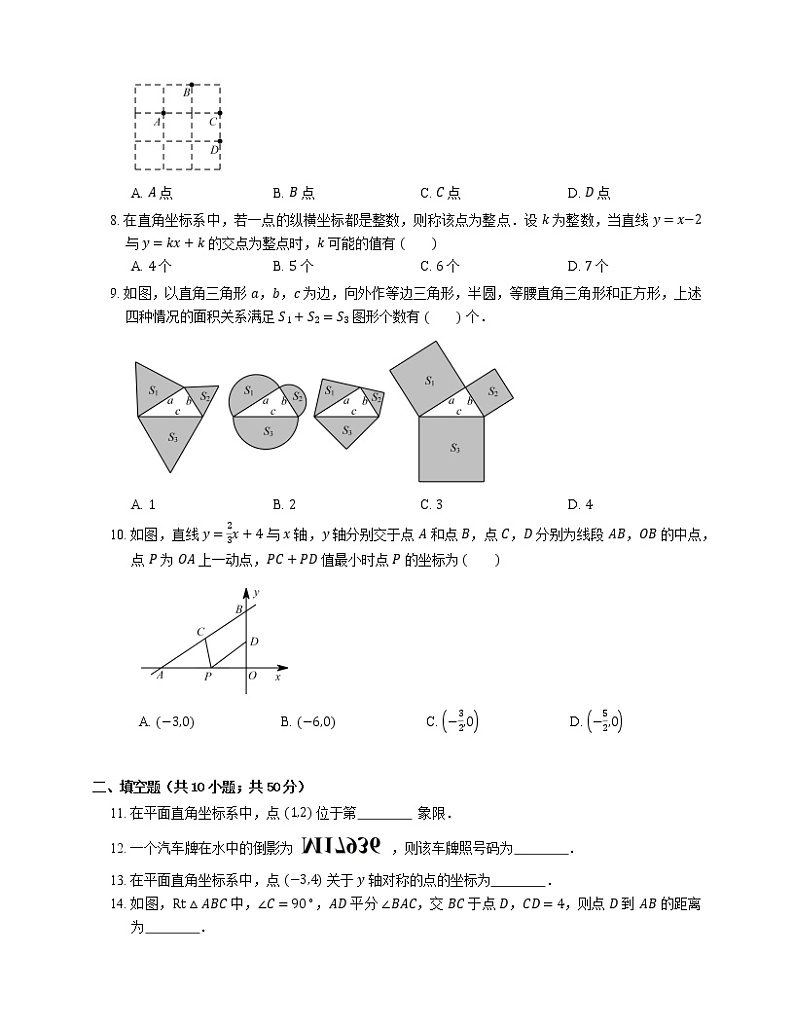
7. 如图，在 3×3 的正方形网格中有四个格点 A，B，C，D，以其中一点为原点，网格线所在直线为坐标轴，建立平面直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点是
A. A 点B. B 点C. C 点D. D 点

8. 在直角坐标系中，若一点的纵横坐标都是整数，则称该点为整点．设 k 为整数，当直线 y=x−2 与 y=kx+k 的交点为整点时，k 可能的值有
A. 4 个B. 5 个C. 6 个D. 7 个

9. 如图，以直角三角形 a，b，c 为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足 S1+S2=S3 图形个数有 个．
A. 1B. 2C. 3D. 4

10. 如图，直线 y=23x+4 与 x 轴，y 轴分别交于点 A 和点 B，点 C，D 分别为线段 AB，OB 的中点，点 P 为 OA 上一动点，PC+PD 值最小时点 P 的坐标为
A. −3,0B. −6,0C. −32,0D. −52,0

二、填空题（共10小题；共50分）
11. 在平面直角坐标系中，点 1,2 位于第 象限．

12. 一个汽车牌在水中的倒影为，则该车牌照号码为 ．

13. 在平面直角坐标系中，点 −3,4 关于 y 轴对称的点的坐标为 ．

14. 如图，Rt△ABC 中，∠C=90∘，AD 平分 ∠BAC，交 BC 于点 D，CD=4，则点 D 到 AB 的距离为 ．

15. 如图，已知 △ABC 是等边三角形，点 B，C，D，E 在同一直线上，且 CG=CD，DF=DE，则 ∠E= 度．

16. 已知 2a+12+b−1=0，则 −a2+b2016= ．

17. 如图，在 Rt△ABC 中，∠B=90∘，AC 的垂直平分线 DE 分别交 AB，AC 于 D，E 两点，若 AB=4，BC=3，则 CD 的长为 ．

18. 如图甲，对于平面上不大于 90∘ 的 ∠MON，我们给出如下定义：如果点 P 在 ∠MON 的内部，作 PE⊥OM，PF⊥ON，垂足分别为点 E，F，那么称 PE+PF 的值为点 P 相对于 ∠MON 的“点角距离”，记为 dP,∠MON．如图乙，在平面直角坐标系 xOy 中，点 P 在第一象限内，且点 P 的横坐标比纵坐标大 1，对于 ∠xOy，满足 dP,∠xOy=5，点 P 的坐标是 ．

19. 如图，已知函数 y=x−2 和 y=−2x+1 的图象交于点 P，根据图象可得方程组 x−y=2,2x+y=1 的解是 ．

20. 某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后缷完物品再另装货物共用 45 分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为 60 千米/时，两车之间的距离 y（千米）与货车行驶时间 x（小时）之间的函数图象如图所示，现有以下 4 个结论：
①快递车从甲地到乙地的速度为 100 千米/时；
②甲、乙两地之间的距离为 120 千米；
③图中点 B 的坐标为 334,75；
④快递车从乙地返回时的速度为 90 千米/时，以上 4 个结论正确的是 ．

三、解答题（共9小题；共117分）
21. 计算下列各题．
（1）∣−2∣+3−π0−2−1+3−27；
（2）∣1−2∣+∣2−3∣+∣3−2∣．

22. 如图，在 △ABC 中，∠BAC 的平分线与 BC 的垂直平分线 PQ 相交于点 P，过点 P 分别作 PN⊥射线AB 于 N，PM⊥AC 于点 M，求证：BN=CM．

23. 如图，已知一架竹梯 AB 斜靠在墙角 MON 处，竹梯 AB=13 m，梯子底端离墙角的距离 BO=5 m．
（1）求这个梯子顶端 A 距地面有多高；
（2）如果梯子的顶端 A 下滑 4 m 到点 C，那么梯子的底部 B 在水平方向上滑动的距离 BD=4 m 吗?为什么?

24. 如图表示一个正比例函数与一个一次函数的图象，它们交于点 A4,3，一次函数的图象与 y 轴交于点 B，且 OA=OB，求这两个函数的解析式．

25. 如图，在四边形 ABCD 中，AD∥BC，E 是 AB 的中点，连接 DE 并延长交 CB 的延长线于点 F，点 G 在边 BC 上，且 ∠GDF=∠ADF．
（1）求证：△ADE≌△BFE；
（2）连接 EG，判断 EG 与 DF 的位置关系并说明理由．

26. 小明根据某个一次函数关系式填写了下面的这张表：
x−2墨水遮盖01y3−110
其中有一格不慎被墨迹遮住了，想想看，该空格里原来填的数是多少?写出你的理由．

27. 一农民带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图所示，结合图象回答下列问题．
（1）农民自带的零钱是多少?
（2）试求降价前 y 与 x 之间的关系式?
（3）由表达式你能求出降价前每千克的土豆价格是多少?
（4）降价后他按每千克 0.4 元将剩余土豆售完，这时他手中的钱（含备用零钱）是 26 元，试问他一共带了多少千克土豆?

28. 已知，点 P 是 Rt△ABC 斜边 AB 上一动点（不与 A，B 重合），分别过 A，B 向直线 CP 作垂线，垂足分别为 E，F，Q 为斜边 AB 的中点．
（1）如图 1，当点 P 与点 Q 重合时，AE 与 BF 的位置关系是 ，QE 与 QF 的数量关系是 ；
（2）如图 2，当点 P 在线段 AB 上不与点 Q 重合时，试判断 QE 与 QF 的数量关系，并给予证明；
（3）如图 3，当点 P 在线段 BA（或 AB）的延长线上时，此时（2）中的结论是否成立?请画出图形并给予证明．

29. 在社会主义新农村建设中，衢州某乡镇决定对 A，B 两村之间的公路进行改造，并由甲工程队从 A 村向 B 村方向修筑，乙工程队从 B 村向 A 村方向修筑．已知甲工程队先施工 3 天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务由甲工程队单独完成，直到公路修通．下图是甲、乙两个工程队修公路的长度 y（米）与施工时间 x（天）之间的函数图象，请根据图象所提供的信息解答下列问题：
（1）乙工程队每天修公路多少米?
（2）分别求甲、乙工程队修公路的长度 y（米）与施工时间 x（天）之间的函数关系式．
（3）若该工程由甲、乙两工程队一直合作施工，需几天完成?
答案
第一部分
1. A
2. A
3. C
4. C
5. C
【解析】A．3−27=−3；B．2−10=1；C．8=22；D．−22=2．
6. C
7. B【解析】以每个点为原点，确定其余三个点的坐标，找出满足条件的点，得到答案．
8. A
9. D
10. C
第二部分
11. 一
12. M17936
13. 3,4
14. 4
15. 15
16. 34
17. 258
18. 3,2
19. x=1,y=−1
20. ①③④
第三部分
21. （1） 原式=2+1−12−3=−12;
（2） 原式=2−1+3−2+2−3=1.
22. 连接 PB，PC，如图，
∵AP 是 ∠BAC 的平分线，PN⊥射线AB，PM⊥AC，
∴PM=PN，∠PMC=∠PNB=90∘，
∵P 在 BC 的垂直平分线上，
∴PC=PB，
在 Rt△PMC 和 Rt△PNB 中，
PC=PB,PM=PN,
∴Rt△PMC≌Rt△PNB，
∴BN=CM．
23. （1） ∵ AO⊥DO，
∴ 在 Rt△ABO 中，AO=AB2−BO2=132−52=12m，
∴ 梯子顶端距地面 12 m．
（2） 滑动不等于 4 m，理由如下：
∵ AC=4 m，
∴ OC=AO−AC=8m，
∴ OD=CD2−OC2=132−82=105m，
∴ BD=OD−OB=105−5m>4 m，
∴ 滑动不等于 4 m．
24. 设正比例函数是 y=mx，设一次函数是 y=kx+b．
∵ 点 A 为两个函数的交点，
∴ 把 A4,3 代入 y=mx 得：4m=3，即 m=34．
∴ 正比例函数是 y=34x；
∵ 点 A 为两个函数的交点，
∴ 把 4,3 代入 y=kx+b，
得：4k+b=3. ⋯⋯①
∵ A4,3，
∴ 根据勾股定理，得 OA=5，
∴ OB=OA=5，
∴ b=−5．
把 b=−5 代入 ①，得 k=2．
∴ 一次函数解析式是 y=2x−5．
25. （1） ∵AD∥BC，
∴∠ADE=∠BFE，
∵E 为 AB 的中点，
∴AE=BE，
在 △ADE 和 △BFE 中，
∠ADE=∠BFE,∠AED=∠BEF,AE=BE,
∴△ADE≌△BFEAAS．
（2） EG 与 DF 的位置关系是 EG 垂直于 DF，
理由为：连接 EG，
∵∠GDF=∠ADE，∠ADE=∠BFE，
∴∠GDF=∠BFE，
∴DG=FG．
由（1）△ADE≌△BFE 得：DE=FE，即 GE 为 DF 上的中线，
∴GE 垂直于 DF．
26. 空格里原来填的数是 2，理由如下：
设一次函数为 y=kx+b，根据图中的信息得 3=−2k+b,1=b,
解得 k=−1,b=1,
∴y=−x+1，
当 y=−1 时，−1=−x+1，x=2，
∴ 空格里原来填的数是 2．
27. （1） 根据图象与 y 轴的交点可知：农民自带的零钱是 5 元．
（2） 设降价出售前，农民手中的钱数与售出的土豆千克数的关系为：y=kx+b，
把点 0,5，30,20 代入可得：b=5,30k+b=20,
解得：k=12,b=5,
∴y=12x+5．
（3） 根据（2）中的表达式：k=12，
∴ 降价前每千克的土豆价格是 12 元．
（4） 26−20÷0.4=15（千克），
15+30=45（千克），
所以一共带了 45 千克土豆．
28. （1） AE∥BF；QE=QF
（2） QE=QF．
证明：延长 EQ 交 BF 于 D，如图，
∵ AE⊥CP，BF⊥CP，
∴ AE∥BF，
∴ ∠AEQ=∠BDQ，
在 △AEQ 和 △BDQ 中，
∠AQE=∠BQD,∠AEQ=∠BDQ,AQ=BQ,
∴ △AEQ≌△BDQ，
∴ EQ=DQ，
∵ ∠BFE=90∘，
∴ QE=QF；
（3） 当点 P 在线段 BA（或 AB）的延长线上时，此时（2）中的结论成立，
证明：延长 EQ 交 FB 于 D，如图，
∵ AE∥BF，
∴ ∠AEQ=∠BDQ，
在 △AEQ 和 △BDQ 中，
∠AQE=∠BQD,∠AEQ=∠BDQ,AQ=BQ,
∴ △AEQ≌△BDQ，
∴ EQ=DQ，
∵ ∠BFE=90∘，
∴ QE=QF．
29. （1） ∵720÷9−3=120，
∴ 乙工程队每天修公路 120 米．
（2） 设 y乙=kx+b .
则 3k+b=0,9k+b=720,
∴k=120,b=−360.
∴y乙=120x−360．
当 x=6 时，y乙=360，
设 y甲=kx，
则 360=6k,k=60，
∴y甲=60x．
（3） 当 x=15 时，y甲=900，
∴ 该公路总长为：720+900=1620（米）．
设需 m 天完成，由题意得，120+60m=1620，
解得 m=9．
答：需 9 天完成．