2020-2021学年北京市西城区北京四中八下期中数学试卷

这是一份2020-2021学年北京市西城区北京四中八下期中数学试卷，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题；共50分）
1. 要使 x+1 有意义，则 x 的取值范围为
A. x≤0B. x≥0C. x≥−1D. x≤−1

2. 平行四边形的一边长为 6 cm，周长为 28 cm，则这条边的邻边长是
A. 22 cmB. 16 cmC. 11 cmD. 8 cm

3. 下列各式中正确的是
A. 27=33B. −22=−2
C. −4=−2D. 16=±4

4. 如图，在菱形 ABCD 中，AB=5，∠BCD=120∘，则对角线 AC 等于
A. 5B. 10C. 15D. 20

5. 下列各组数据中的三个数，可作为三边长构成直角三角形的是
A. 2，3，4B. 4，5，6C. 8，15，17D. 11，12，13

6. 在下列条件中，不能判定四边形为平行四边形的是
A. 一组对边平行且相等B. 两组对边分别平行
C. 一组对边平行，另一组对边相等D. 对角线互相平分

7. 我们把形如 ax+b（a，b 为有理数，x 为最简二次根式）的数叫做 x 型无理数，如 25+3 是 5 型无理数，则 2+62 是
A. 2 型无理数B. 3 型无理数C. 6 型无理数D. 12 型无理数

8. 如图，点 O 为矩形 ABCD 的对角线交点，点 E 从点 A 出发沿 AB 向点 B 运动，移动到点 B 停止，延长 EO 交 CD 于点 F，则四边形 AECF 形状的变化依次为
A. 平行四边形 → 正方形 → 平行四边形 → 矩形
B. 平行四边形 → 菱形 → 平行四边形 → 矩形
C. 平行四边形 → 正方形 → 菱形 → 矩形
D. 平行四边形 → 菱形 → 正方形 → 矩形

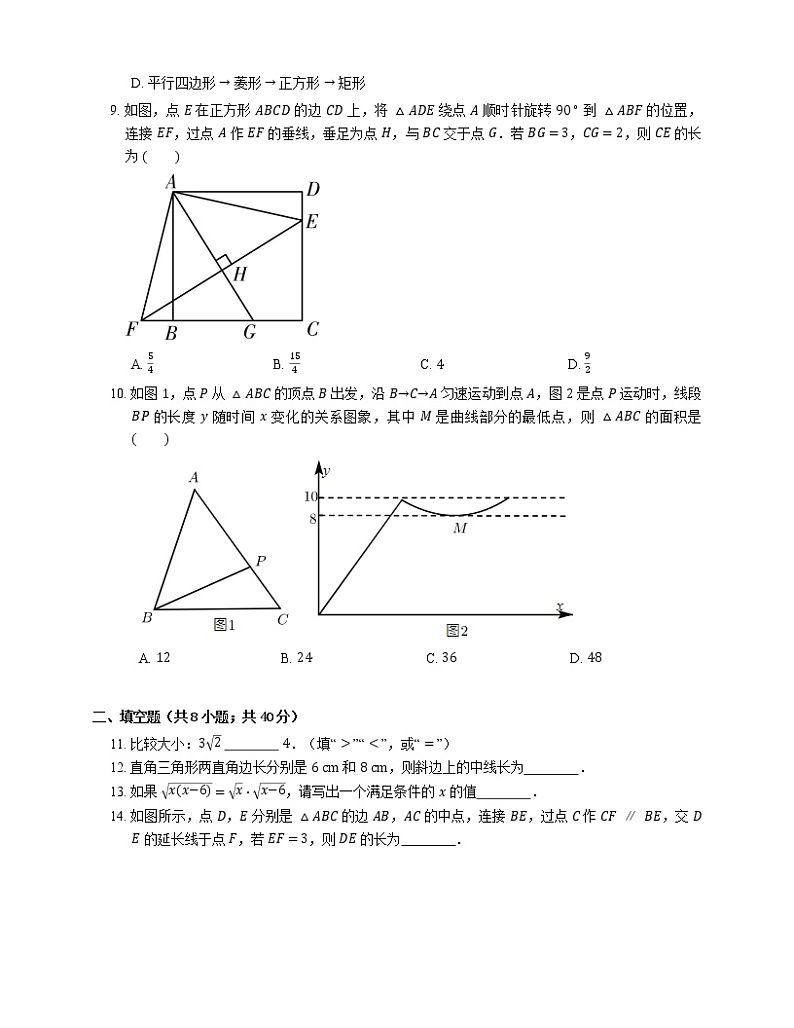
9. 如图，点 E 在正方形 ABCD 的边 CD 上，将 △ADE 绕点 A 顺时针旋转 90∘ 到 △ABF 的位置，连接 EF，过点 A 作 EF 的垂线，垂足为点 H，与 BC 交于点 G．若 BG=3，CG=2，则 CE 的长为
A. 54B. 154C. 4D. 92

10. 如图 1，点 P 从 △ABC 的顶点 B 出发，沿 B→C→A 匀速运动到点 A，图 2 是点 P 运动时，线段 BP 的长度 y 随时间 x 变化的关系图象，其中 M 是曲线部分的最低点，则 △ABC 的面积是
A. 12B. 24C. 36D. 48

二、填空题（共8小题；共40分）
11. 比较大小：32 4．（填“>”“16，
∴32>4．
12. 5 cm
【解析】由勾股定理得，斜边长为：62+82=10，
则斜边上的中线长为：12×10=5 cm．
13. 8
【解析】如果 xx−6=x⋅x−6，
根据二次根式下的数的非负性可知，
xx−6>0，x>0，x−6>0，
由 xx−6>0 可得：x0，即 x6，
由 x>0，x−6>0 得：x>6，
∴x 得取值范围为：x>6，
则写一个满足条件得 x 的值为：8．
故答案为：8．（答案不唯一，x 的值 >6 即可．）
14. 32
【解析】∵D，E 分别是 △ABC 的边 AB，AC 的中点，
∴DE 为 △ABC 的中位线，
∴DE∥BC，DE=12BC，
∵CF∥BE，
∴ 四边形 BCFE 为平行四边形，
∴BC=EF=3，
∴DE=12BC=32．
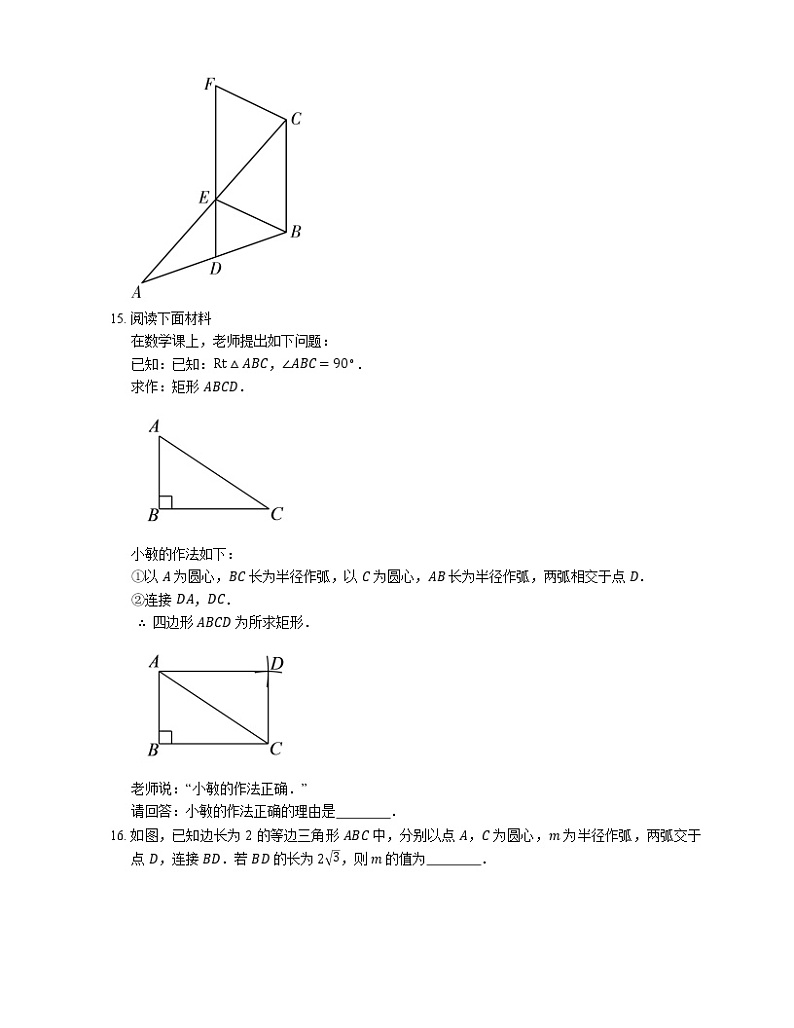
15. 两组对边分别相等的四边形是平行四边形，有一个角是直角的平行四边形是矩形
16. 2 或 27
【解析】由作图知，点 D 在 AC 的垂直平分线上，
∵△ABC 是等边三角形，
点 B 在 AC 的垂直平分线上，
BD 垂直平分 AC，
设垂足为 E，
∵AC=AB=2，
∴BE=3，
当点 D，B 在 AC 的两侧时，如图，
∵BD=23，
∴BE=DE，
∴AD=AB=2，
∴m=2；
当点 D，B 在 AC 的同侧时，如图，
∵BDʹ=23，
∴DʹE=33，
∴ADʹ=332+12=27，
∴m=27，
综上所述，m 的值为 2 或 27．
17. ②
【解析】∵x2−4x−12=0 即 xx−4=12，
∴ 构造如图②中大正方形的面积是 x+x−42，
其中它又等于四个矩形的面积加上中间小正方形的面积，即 4×12+42，
据此易得 x=6．
18. ①②③④
【解析】平面内任意取一点 D，与点 A，点 B，点 C 构成四边形 ABCD，
∵M，N，P，Q 分别是 AB，BC，CD，DA 的中点，
∴MN∥AC，MN=12AC，PQ∥AC，PQ=12AC，
MQ∥BD，MQ=12BD，PN∥BD，PN=12BD，
∴MN∥PQ，MN=PQ，MQ∥PN，MQ=PN，
∴ 四边形 MNPQ 是平行四边形，
∴ 存在无数个中点四边形 MNPQ 是平行四边形，故①正确；
当 AC=BD 时，即以 B 为圆心，AC 为半径画圆，
在圆弧上取一点 D，则有 MQ=PQ=PN=MN，
∴ 四边形 MNPQ 是菱形，
∴ 存在无数个中点四边形 MNPQ 是菱形，故②正确；
当 BD⊥AC 时，MQ⊥AC，PQ⊥MQ，即 ∠PQM=90∘，
∴ 四边形 MNPQ 是矩形，
∴ 存在无数个中点四边形是矩形，故③正确；
当且仅当 BD⊥AC 时，BD=AC 时，
中点四边形 MNPQ 才是正方形，这样的点 D 只有 2 个，
故存在两个中点四边形 MNPQ 是正方形，故④正确．
∴ 正确的是①②③④．
第三部分
19. （1） 原式=22−32+1+2−1=−322.
（2） 原式=6+7−5=6+2.
20. （1）
x2−2x=0.xx−2=0.x1=0,x2=2.
（2）
x2−8x+1=0.x2−8x+16=15.x−42=15.x−4=±15.x1=4+15,x2=4−15.
21. 证法一：
∵ 四边形 ABCD 为平行四边形
∴AD∥BC，AD=BC，
∴∠1=∠2，
∴∠3=∠4，
∵BE=DF，
∴△ADF≌△CBESAS，
∴AF=CE，
【解析】证法二：
连接 AC 交 BD 于点 O，连接 AE，CF，
∵ 四边形 ABCD 为平行四边形
∴OA=OC，OB=OD
∵BE=DF
∴OD+DF=OB+BE 即 OF=OE，
∴ 四边形 AECF 是平行四边形
∴AF=CE．
22. （1） 如图 △ABC 即所求：
（2） 2
【解析】设 AC 边上高为 h，
∵S△ABC=4×4−12×3×4−12×1×2−12×2×4=16−6−1−4=5,
又 ∵S△ABC=12AC⋅h，
∴h=2S△ABCAC=2×55=2，
即 AC 边上的高为 2．
（3） 如图 △DEF 即所求．（答案不唯一）
23. x1=−2，x2=1（不合题意，舍）；x1=2，x2=−2；x1=−3，x2=2
24. （1） 如图，连接 AC 交 BD 于点 O，连接 CF．
∵FG 垂直平分 CE，
∴CF=EF．
∵ 四边形 ABCD 为菱形，
∴AC⊥BD，OA=OC，
∴BD 垂直平分 AC，
∴CF=AF，
∴AF=EF．
（2） 30∘，12
【解析】①如图，延长 EF，交 DC 于 H，
∵∠CFH=∠FCE+∠FEC，∠AFH=∠FAE+∠FEA，
∴∠AFC=∠FCE+∠FEC+∠FAE+∠FEA．
∵BD 垂直平分 AC，
∴∠AFD=∠CFD=12∠AFC．
∵AF=CF=EF，
∴∠AEF=∠EAF，∠FEC=∠FCE，
∴∠AFD=∠FAE+∠ABF=∠FEA+∠CEF，
∴∠ABF=∠CEF．
∵∠ABC=60∘，
∴∠ABF=∠CEF=30∘．
②连接 AC，交 BD 于点 O，
∵M 和 N 分别是 AE 和 EF 的中点，点 G 为 CE 中点，
∴MN=12AF，NG=12CF，即 MN+NG=12AF+CF，
∴ 当点 F 与菱形 ABCD 对角线交点 O 重合时，AF+CF 最小，即此时 MN+NG 最小．
∵ 四边形 ABCD 是菱形，
∴AB=BC，
又 ∵∠ABC=60∘，
∴△ABC 为等边三角形，AC=AB=1，
即 MN+NG 的最小值为 12．
25. （1） ∵ 正方形 ABCD 中，AD=DC，∠BAD=∠BCD=90∘，
∴∠CDE+∠EDA=90∘，∠FCD=∠EAD，
又 ∵DE⊥DF，
∴∠FDC+∠CDE=90∘，
∴∠FDC=∠EDA，
在 △FDC 和 △EDA 中，
∠FDC=∠EDA,CD=AD,∠FCD=∠EAD,
∴△FDC≌△EDAASA，
∴DF=DE．
（2） DG=DF．
∵∠FDE=90∘，
∴△DFE 是等腰直角三角形，
∴∠DFE=∠DEF=45∘，
∴∠DEG=45∘+∠FEG，∠DGE=∠BEG+45∘，
又 ∵GE 平分 ∠BEF，
∴∠FEG=∠BEG，
∴∠DEG=∠DGE，
∴DE=DG，
∴DG=DF．
（3） AB−GH=12EF．
【解析】如图，过点 G 作 GM⊥AB，交 AB 于 M，
∵GE 平分 ∠BEF，GM⊥AB，GH⊥EF，
∴GM=GH，
∵ 在正方形 ABCD 中，∠ABG=45∘，
∴△MGB，△ABD 是等腰直角三角形，
即 GB=2GM=2GH，BD=2AB，
由（1）可知 △EDF 是等腰直角三角形，
即 EF=2ED，
∵ED=DG，
∴DG=22EF，
∵BD=BG+DG，
即 2AB=2GH+22EF，
∴AB−GH=12EF．
26. （1） ①点 O 到 △ABC 上任意一点距离为 d点O,△ABC，
由图可知，d点O,△ABC=2．
② P 在 x 轴正半轴，由点到直线垂线段最短可知，
P 在 O 时，最小距离为 d=42=22