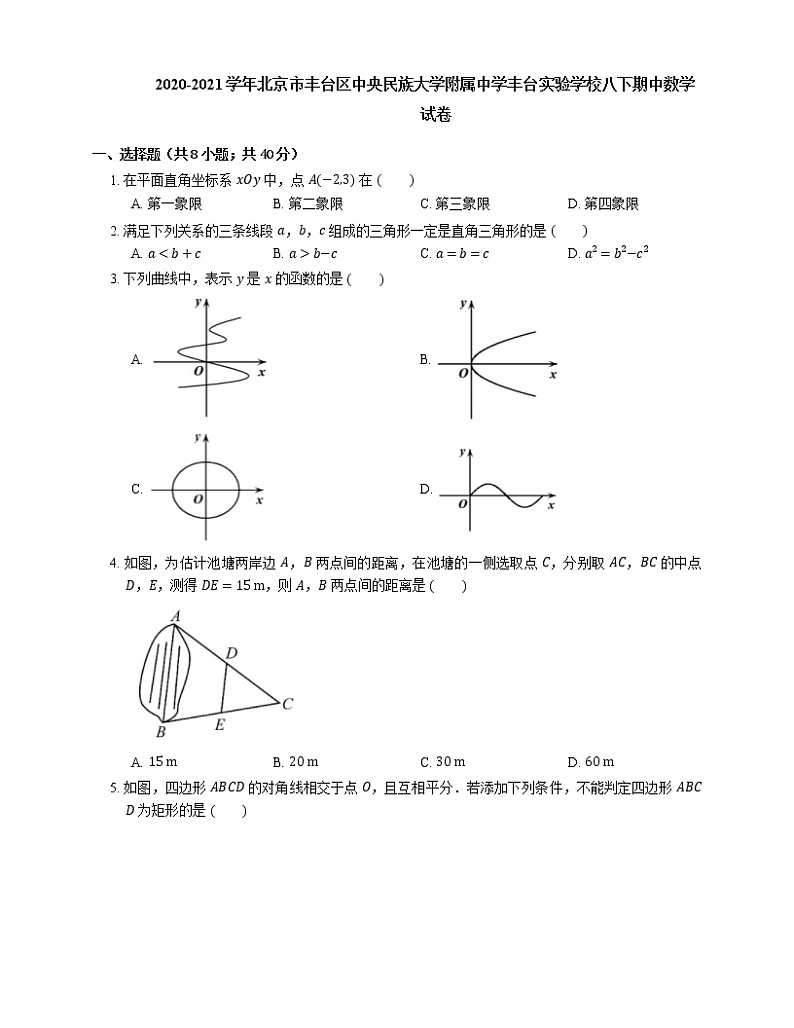

2020-2021学年北京市丰台区中央民族大学附属中学丰台实验学校八下期中数学试卷
展开一、选择题(共8小题;共40分)
1. 在平面直角坐标系 xOy 中,点 A−2,3 在
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
2. 满足下列关系的三条线段 a,b,c 组成的三角形一定是直角三角形的是
A. a
3. 下列曲线中,表示 y 是 x 的函数的是
A. B.
C. D.
4. 如图,为估计池塘两岸边 A,B 两点间的距离,在池塘的一侧选取点 C,分别取 AC,BC 的中点 D,E,测得 DE=15 m,则 A,B 两点间的距离是
A. 15 mB. 20 mC. 30 mD. 60 m
5. 如图,四边形 ABCD 的对角线相交于点 O,且互相平分.若添加下列条件,不能判定四边形 ABCD 为矩形的是
A. AC=BDB. ∠DAB=90∘
C. AB=ADD. ∠ADC+∠ABC=180∘
6. 在平面直角坐标系 xOy 中,如图,四边形 ABCD 是菱形,∠DAB=60∘,点 P 是边 CD 的中点,如果菱形的周长为 16,那么点 P 的坐标是
A. 4,4B. 2,2C. 23,1D. 3,1
7. 《九章算术》内容丰富,与实际生活联系紧密,在书上讲述了这样一个问题“今有垣高一丈,倚木于垣,上与垣齐.引木却行一尺,其木至地.问木长几何?”其内容可以表述为:“有一面墙,高一丈.将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动 1 尺,则木杆上端恰好沿着墙滑落到地面上.问木杆长多少尺?”(说明:1 丈 =10 尺)
设木杆长 x 尺,依题意,下列方程正确的是
A. x2=x−12+102B. x+12=x2+102
C. x2=x−12+12D. x+12=x2+12
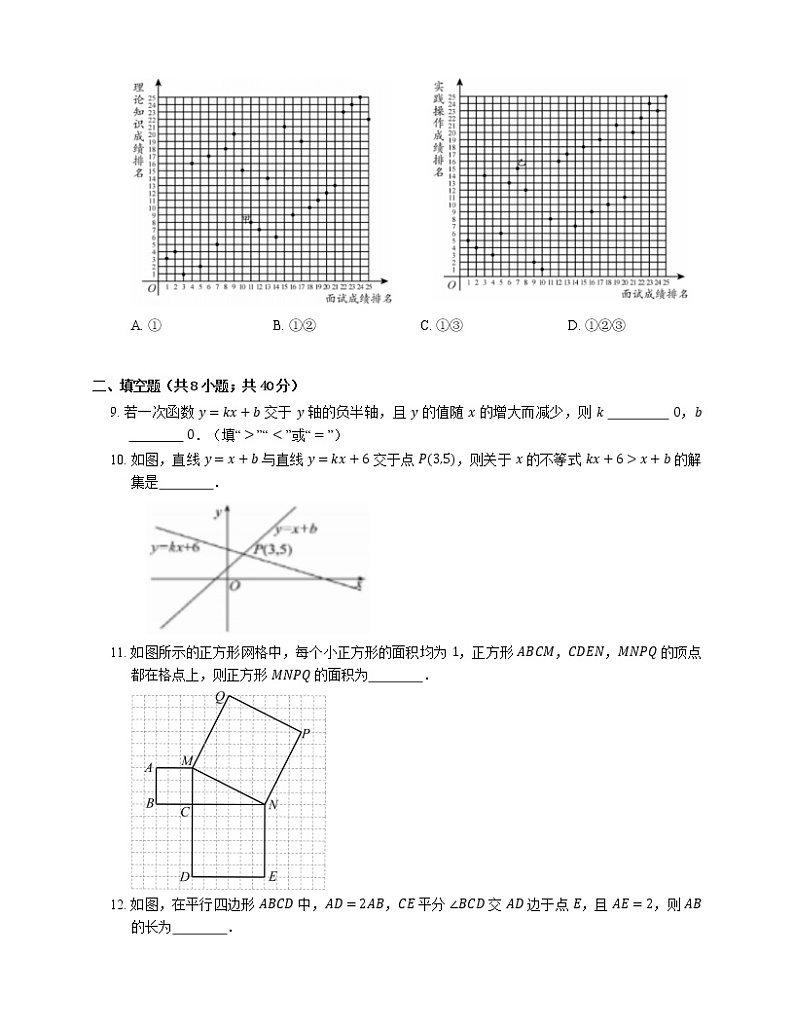
8. 某公司计划招募一批技术人员,他们对 25 名面试合格人员又进行了理论知识和实践操作测试,其中 25 名入围者的面试成绩排名,理论知识成绩排名与实践成绩的排名情况如图所示.下面有 3 个推断:
①甲的理论知识成绩排名比面试成绩排名靠前;
②甲的实践操作成绩排名与理论知识成绩排名相同;
③乙的理论知识成绩排名比甲的理论知识成绩排名靠前.
其中合理的是
A. ①B. ①②C. ①③D. ①②③
二、填空题(共8小题;共40分)
9. 若一次函数 y=kx+b 交于 y 轴的负半轴,且 y 的值随 x 的增大而减少,则 k 0,b 0.(填“>”“<”或“=”)
10. 如图,直线 y=x+b 与直线 y=kx+6 交于点 P3,5,则关于 x 的不等式 kx+6>x+b 的解集是 .
11. 如图所示的正方形网格中,每个小正方形的面积均为 1,正方形 ABCM,CDEN,MNPQ 的顶点都在格点上,则正方形 MNPQ 的面积为 .
12. 如图,在平行四边形 ABCD 中,AD=2AB,CE 平分 ∠BCD 交 AD 边于点 E,且 AE=2,则 AB 的长为 .
13. 在菱形 ABCD 中,∠A=60∘,其所对的对角线长为 2,则菱形 ABCD 的面积是 .
14. 下列命题,①对顶角相等;②两直线平行,同位角相等;③平行四边形的对角相等.其中逆命题是真命题的命题共有 个.
15. 在平面直角坐标系 xOy 中,若直线 y=2x+3 向下平移 n 个单位长度后,与直线 y=−x+2 的交点在第一象限,则 n 的取值范围是 .
16. 自 2020 年 1 月 1 日延庆区开展创城以来,积极推广垃圾分类,在垃圾分类指导员的帮助下,居民的投放正确率不断提升,分类习惯正在养成.尤其是在 5 月 1 日新版《北京市生活垃圾管理条例》实施以来,延庆区城管委为全区从源头上规范垃圾投放,18 个街乡镇新配备户用分类垃圾桶 20 万个,助力推进垃圾分类.
下面两张图表是某小区每个月的厨余垃圾量和其他垃圾量.
(1)3 月份厨余垃圾量比其他垃圾量多 吨;
(2) 月份两类垃圾量(单位:吨)的差距最大.
三、解答题(共9小题;共117分)
17. 下面是小明设计的“作菱形 ABCD”的尺规作图过程.
求作:菱形 ABCD.
作法:
①作线段 AC;
②作线段 AC 的垂直平分线 l,交 AC 于点 O;
③在直线 l 上取点 B,以 O 为圆心,OB 长为半径画弧,交直线 l 于点 D(点 B 与点 D 不重合);
④连接 AB,BC,CD,DA.
所以四边形 ABCD 为所求作的菱形.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:
∵OA=OC,OB=OD,
∴ ,
∵ ,
∴ 四边形 ABCD 为菱形( )(填推理的依据).
18. 已知:一次函数的图象经过点 A4,3 和 B−2,0.
(1)求这个一次函数的表达式;
(2)求一次函数与 y 轴的交点.
19. 如图,点 E,F 在平行四边形 ABCD 的对角线 AC 上,且 AE=CF.
求证:DE=BF.
20. 如图,四边形 ABCD 中,AB=CD,AD=BC,对角线 AC,BD 相交于点 O,且 OA=OD,求证:四边形 ABCD 是矩形.
21. 如图,在平面直角坐标系 xOy 中,直线 y=−32x+bk≠0 与 x 轴交于 A,与 y 轴交于 B0,3.
(1)求该直线的表达式和点 A 的坐标;
(2)若 x 轴一点 C,且 S△ABC=6,直接写出点 C 的坐标.
22. 自开展全区读书宣传活动以来,某书店出租店生意非常火爆,为此开设两种租书方式,方式一:零星租书,每本收费 1 元;
方式二:会员卡租书,会员每月交会员费 12 元,租书费每本 0.4 元.
小彬经常来该店租书,若小彬每月租书数量为 x 本,每月应付的租书金额为 y 元.
(1)分别写出两种租书方式下,y 与 x 之间的函数关系;
(2)若小彬在一月内为班级租 25 本书,试问选用哪种租书方式合算?
23. 如图,平行四边形 ABCD 中,AB=8 cm,BC=3 cm,E 是 DC 中点,P 是线段 AB 上一动点,连接 PE,设 P,A 两点间的距离为 x cm,P,E 两点间的距离为 y cm.(当点 P 与点 A 重合时,x 的值为 0)
小东根据学习一次函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行了探究.
下面是小东的探究过程:
(1)通过取点、画图、测量,得到了 x 与 y 的几组值,如下表,请补充完整:(说明:相关数值保留一位小数);
x/
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:
①当 y 取最小值时,x 的值约为 cm.(结果保留一位小数)
②当 △APE 是等腰三角形时,PA 的长度约为 cm.(结果保留一位小数)
24. 如图,四边形 ABCD 是正方形,点 E 是边 BC 的任意一点,连接 AE,过点 B 做 BH⊥AE,垂足为 H,交 CD 于点 P,将线段 PC 绕着点 P 逆时针旋转 90∘ 得到线段 PQ,连接 EQ,
(1)补全图形;
(2)写出 AE 与 EQ 的数量关系,并加以证明.
25. 直线 l1:y=kx+bk≠0,与直线 l2:y=ax 相交于点 B1,2.
(1)求直线 l2 的解析式;
(2)横、纵坐标都是整数的点叫做整点.记直线 l1 与直线 l2 和 x 轴围成的区域内(不含边界)为 W.
①当 k=−1 时,直接写出区域 W 内的整点个数;
②若区域 W 内的整点恰好为 2 个,结合函数图象,求 k 的取值范围.
答案
第一部分
1. B
2. D
3. D
4. C
5. C
【解析】∵ 四边形 ABCD 的对角线相交于点 O,且互相平分,
∴ 四边形 ABCD 是平行四边形,
若 AC=BD,则四边形 ABCD 是矩形,
故选项A不符合题意;
若 ∠DAB=90∘,则四边形 ABCD 是矩形,
故选项B不符合题意;
若 AB=AD,则四边形 ABCD 是菱形,
故选项C符合题意;
∵ 四边形 ABCD 是平行四边形,
∴∠ADC=∠ABC,
若 ∠ADC+∠ABC=180∘,
∴∠ADC=∠ABC=90∘,
则四边形 ABCD 是矩形,
故选项D不符合题意.
6. D【解析】因为四边形 ABCD 是菱形,菱形的周长为 16,
所以 AD=AB=DC=BC=4,
因为 ∠DAB=60∘,
所以 △ADB 是等边三角形,
所以 DB=4,
所以 OD=2,OC=CD2−OD2=23,
过 P 作 PE⊥OD,PF⊥OC,垂足分别为 E,F,如图,
所以 PE∥OC,PF∥OD,
因为点 P 是边 CD 的中点,
所以 PE,PF 是三角形 OCD 的中位线,
所以 PE=12OC=3,PF=12OD=1.
所以点 P 的坐标为 3,1,
故选:D.
7. A
8. D
第二部分
9. <,<
10. x<3
11. 45
12. 2
13. 23
14. 2
15. 1
第三部分
17. (1) 略
(2) 四边形 ABCD 为平行四边形;AC⊥BD;对角线互相垂直的平行四边形是菱形
18. (1) y=12x+1
(2) 0,1
19. 略
20. 略
21. (1) y=−32x+3;A2,0.
(2) C−2,0 或 C6,0.
22. (1) y=x;y=0.4x+12
(2) 选方式 2
23. (1)
x/
(2) 略
(3) ① 5.7;② 3.3 或 6.3
24. (1) 略
(2) AE=EQ
证明略
25. (1) 略.
(2) ① 1 个;
② −1
2020-2021学年北京市丰台区第十二中学八下期中数学试卷: 这是一份2020-2021学年北京市丰台区第十二中学八下期中数学试卷,共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018_2019学年北京市丰台区八下期末数学试卷: 这是一份2018_2019学年北京市丰台区八下期末数学试卷,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年北京市丰台区九下期末数学试卷: 这是一份2020-2021学年北京市丰台区九下期末数学试卷,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












