2020-2021学年上海市浦东新区上南中学南校八下期中数学试卷

这是一份2020-2021学年上海市浦东新区上南中学南校八下期中数学试卷，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共6小题；共30分）
1. 下列函数中，一次函数是
A. y=1x−1B. y=x2+2
C. y=xD. y=kx+b （ k，b 是常数）．

2. 已知一次函数 y=kx+b 的图象经过第一、三、四象限，且与 x 轴交于点 3,0，则关于 x 的不等式 kx+b>0 的解集为
A. x<−3B. x>−3C. x>3D. x<3

3. 下列方程有实数根的是
A. 2+x2=0B. x3+5=0C. xx−1=1x−1D. x2+x+2=0

4. 下列方程组中，属于二元二次方程组的是
A. x−2=y,3x+y=5B. x+2y=1,x+3y2=1
C. 2x+y+1x−y=1,1x+y−1x−y=−2D. x−y=1,x2+xy=2

5. 已知一个多边形的内角和小于它的外角和，那么这个多边形是
A. 三角形B. 四边形C. 五边形D. 六边形

6. 在下列命题中，真命题是
A. 四个内角为 80∘，100∘，80∘ 和 100∘ 的四边形是平行四边形
B. 一组对边平行，一组对角相等的四边形是平行四边形
C. 一组对边平行，另一组对边相等的四边形是平行四边形
D. 一条对角线被另一条对角线平分的四边形是平行四边形

二、填空题（共12小题；共60分）
7. 直线 y=x−2 在 y 轴上的截距是 ．

8. 已知直线 y=kx+b 与直线 y=2x+6 平行，且经过点 0,3，那么该直线的表达式是 ．

9. 若关于自变量 x 的一次函数 y=2m−1x+m−4 的图象不经过第二象限，则 m 的取值范围是 ．

10. 若 Ax1,y1，Bx2,y2 是一次函数 y=2x−1 图象上的不同的两点，则 x1−x2y1−y2 0．（填“>”，“=”或“<”）

11. 关于 x 的方程 ax+3=2x+1（其中 a≠2）的解是 ．

12. 用换元法解分式方程 xx2−1+2x2−2x=35 时，若设 xx2−1=y，则原方程可以化为整式方程 ．

13. 如果关于 x 的无理方程 x+2+5+m=0 没有实数根，那么 m 的取值范围是 ．

14. 在直角坐标平面内到 A−6,0，B10,0 的距离都等于 10 的点的坐标是 ．

15. 在平行四边形 ABCD 中，∠A:∠B=2:3，则 ∠C= ．

16. 若一个多边形一共可以作出 5 条对角线，那么这个多边形的内角和是 ．

17. 如图，在平行四边形 ABCD 中，若已知 AM=4，∠ADC 和 ∠BCD 的平分线分别交 AB 于点 N，M，那么 BN= ．

18. 如图，已知直线 y=−3x+3 与 x 轴交于点 A，与 y 轴交于点 B，以线段 AB 为边在直线 AB 的右侧作以 AB 为直角边的等腰 Rt△ABC，则直线 BC 的表达式为 ．

三、解答题（共8小题；共104分）
19. 解方程 52−x+20x2−4=1．

20. 解方程：x−5+x+4=3．

21. 解方程组 x2+xy−2y2=0,x2+6xy+9y2=4.

22. 已知A，B两地之间的距离为 400 千米，甲、乙两车同时从A城出发沿着一公路驶向B城，已知甲车去的时候平均速度是 100 千米/时，甲车到达B城 1 小时后沿原路返回．如图是两车离A城的路程 y（千米）与行驶时间 x（小时）之间的函数图象．
（1）图中 a= ，b= ．
（2）甲车返回过程中 y 与 x 之间的函数解析式是 ．
（3）若乙车行驶 6 小时与返回的甲车相遇，则点 C 的坐标是 ，乙车到达B地共用了 小时．

23. 某市一个公园要改造维修，若由甲、乙两个工程队合作，12 天可以完成；若甲工程队先单独做 5 天后，乙队也来参加，两队再合作 9 天可以完工，问若两队单独完成这项工程各需几天?

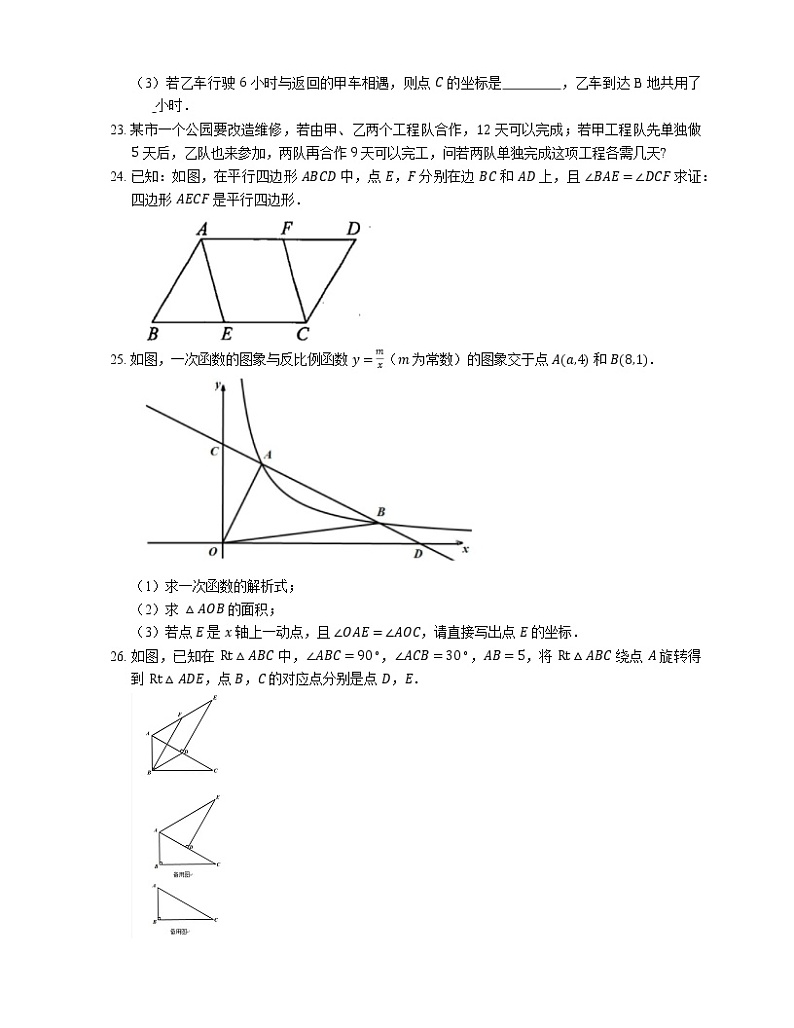
24. 已知：如图，在平行四边形 ABCD 中，点 E，F 分别在边 BC 和 AD 上，且 ∠BAE=∠DCF 求证：四边形 AECF 是平行四边形．

25. 如图，一次函数的图象与反比例函数 y=mx（m 为常数）的图象交于点 Aa,4 和 B8,1．
（1）求一次函数的解析式；
（2）求 △AOB 的面积；
（3）若点 E 是 x 轴上一动点，且 ∠OAE=∠AOC，请直接写出点 E 的坐标．

26. 如图，已知在 Rt△ABC 中，∠ABC=90∘，∠ACB=30∘，AB=5，将 Rt△ABC 绕点 A 旋转得到 Rt△ADE，点 B，C 的对应点分别是点 D，E．
（1）当点 D 恰好落在边 AC 上时，若点 F 为 AE 的中点，连接 BD，BF，
①求证：四边形 BDEF 是平行四边形；
②连接 BE，求 BE 的长；
（2）当点 E 落在 AB 边的延长线上时，若直线 DE 与直线 BC 交于点 F，请直接写出 DE，DF，FC 直接的数量关系．
答案
第一部分
1. C
2. C
3. B
4. D
5. A
6. B
第二部分
7. −2
8. y=2x+3
9. 1210. >
11. x=2−3aa−2
12. 5y2−3y+10=0
13. m>−5
14. 2,6 或 2,−6
15. 72∘
16. 540∘
17. 4
18. y=−12x+3 或 y=13x+3
第三部分
19.
x2+5x−14=0,x1=−7,x2=2.
经检验：x=2 是增根，x=−7 是原方程的根．
∴ 原方程的根是 x=−7．
20.
x−5=3−x+4x−5=9−6x+4+x+4x+4=3x=5.
经检验 x=5 为原方程的根，
所以原方程的根为 x=5．
21. 由①得：
x+2y=0或x−y=0.
由②得：
x+3y=2或x+3y=−2.
原方程组可化为
x+2y=0,x+3y=2.x+2y=0,x+3y=−2.x−y=0,x+3y=2.x−y=0,x+3y=−2.
得原方程组的解为 x1=−12,y1=−12.x2=12,y2=12.x3=−4,y3=2.x4=4,y4=−2.
22. （1） 4；5
（2） y=−80x+800
（3） 6,320；7.5
23. 设甲队单独完成需要 x 天，则乙队单独完成需要 y 天．
根据题意，得
12x+12y=1,14x+9y=1.
解得
x=20,y=30.
经检验，x=20,y=30 是原方程的解，且符合题意．
答：甲队单独完成需要 20 天，则乙队单独完成需要 30 天．
24. 在平行四边形 ABCD 中，∠B=∠D，AB=CD，AD=BC，
又 ∵∠BAE=∠DCF，
∴△ABE≌△CDFASA．
∴BE=DF，
∴AF=CE，
又 ∵ 在平行四边形 ABCD 中，AD∥BC 即 AF∥EC，
∴ 四边形 AECF 是平行四边形．
（本题方法不唯一）
25. （1） 根据题意，得 y=8x，
所以 4=8a，即 a=2，
所以 A2,4，
设直线 AB：y=kx+bk≠0，
将 2,4，8,1 代入，
得，k=−12，b=5，
得：y=−12x+5，
（2） 过点 A 作 AH⊥OD 于 H，过点 B 作 BF⊥OD 于 F，
所以 AH=4，BF=1，
令 x=0，得 y=10，
所以 D10,0，
所以 OD=10，
所以 S△AOB=S△AOD−S△OBD=12OD⋅OH−12OD⋅OF，
所以 S△AOB=15，
（本题方法不唯一．）
（3） E12,0；E2−103,0．
26. （1） ①在 Rt△ABC 中，∠C=30∘，AB=5，
∴AC=2AB=10，BC=53，∠BAC=60∘，
∵△ABC 旋转得到 △ADE，
∴AD=AB=5，AE=AC=10，∠DAE=60∘ ，
得 D 为 AC 中点，
∴BD=12AC=5，
∴AD=AB=BD，即 △ABD 是等边三角形，
∴∠ADB=60∘，
∴∠ADB=∠DAE，
∴AF∥BD，
即 EF∥BD，
又 ∵ 点 F 为 AE 中点，
∴EF=5，
∴EF=BD，
∴ 四边形 BDEF 是平行四边形．
②过 B 作 BH 垂直 EA 的延长线于点 H；
∵∠BAE=120∘，
∴∠HAB=60∘，∠HBA=30∘，
在 Rt△ABH 中，AB=5，∠HBA=30∘，
∴AH=52，BH=523，
∴EH=252，
∴ 在 Rt△BEH 中，
BE=BH2+EH2=57．
（2） DE+DF=FC．