2019-2020学年浙江省温州瓯海区外国语学校八上期中数学试卷
展开一、选择题(共10小题;共50分)
1. 下列垃圾分类图表中,是轴对称图形的是
A. B.
C. D.
2. 下列句子是命题的是
A. 画 ∠AOB=45∘B. 小于直角的的角是锐角吗?
C. 连接 CDD. 三边对应相等的两个三角形全等
3. 下列长度的各组线段,能组成三角形的是
A. 1 cm,2 cm,3 cmB. 6 cm,4 cm,5 cm
C. 3 cm,4 cm,8 cmD. 5 cm,2 cm,8 cm
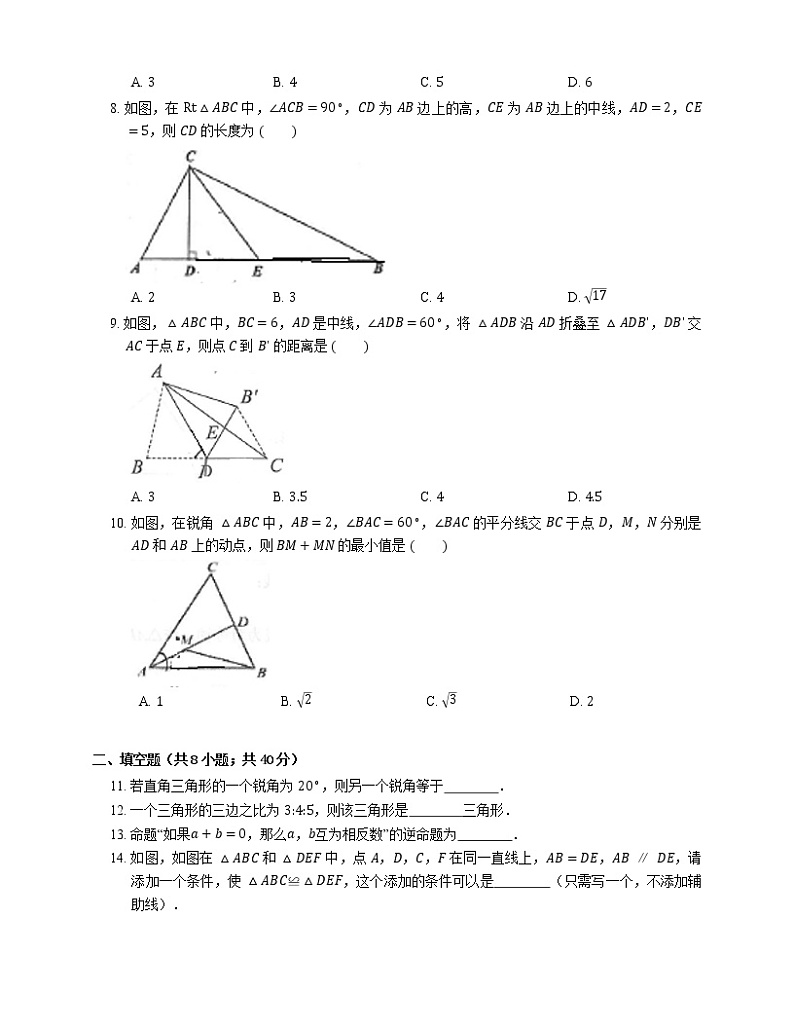
4. 如图,在 △ABC 中,D 是 BC 延长线上一点,∠B=40∘,∠ACD=120∘,则 ∠A 等于
A. 60∘B. 70∘C. 80∘D. 90∘
5. 等腰三角形的两条边长分别是 8 和 4,则它的周长是
A. 12B. 16C. 20D. 16 或 20
6. 能说明命题“若 a>b,则 a2>b2.”是假命题的一个反例可以是
A. a=0,b=−1B. a=2,b=1
C. a=−2,b=−1D. a=0,b=2
7. 如图,在 △ABC 中,∠C=90∘,BD 平分 ∠ABC,交 AC 于点 D.若 BC=6,DC=4,则点 D 到 AB 的距离为
A. 3B. 4C. 5D. 6
8. 如图,在 Rt△ABC 中,∠ACB=90∘,CD 为 AB 边上的高,CE 为 AB 边上的中线,AD=2,CE=5,则 CD 的长度为
A. 2B. 3C. 4D. 17
9. 如图,△ABC 中,BC=6,AD 是中线,∠ADB=60∘,将 △ADB 沿 AD 折叠至 △ADBʹ,DBʹ 交 AC 于点 E,则点 C 到 Bʹ 的距离是
A. 3B. 3.5C. 4D. 4.5
10. 如图,在锐角 △ABC 中,AB=2,∠BAC=60∘,∠BAC 的平分线交 BC 于点 D,M,N 分别是 AD 和 AB 上的动点,则 BM+MN 的最小值是
A. 1B. 2C. 3D. 2
二、填空题(共8小题;共40分)
11. 若直角三角形的一个锐角为 20∘,则另一个锐角等于 .
12. 一个三角形的三边之比为 3:4:5,则该三角形是 三角形.
13. 命题“如果a+b=0,那么a,b互为相反数”的逆命题为 .
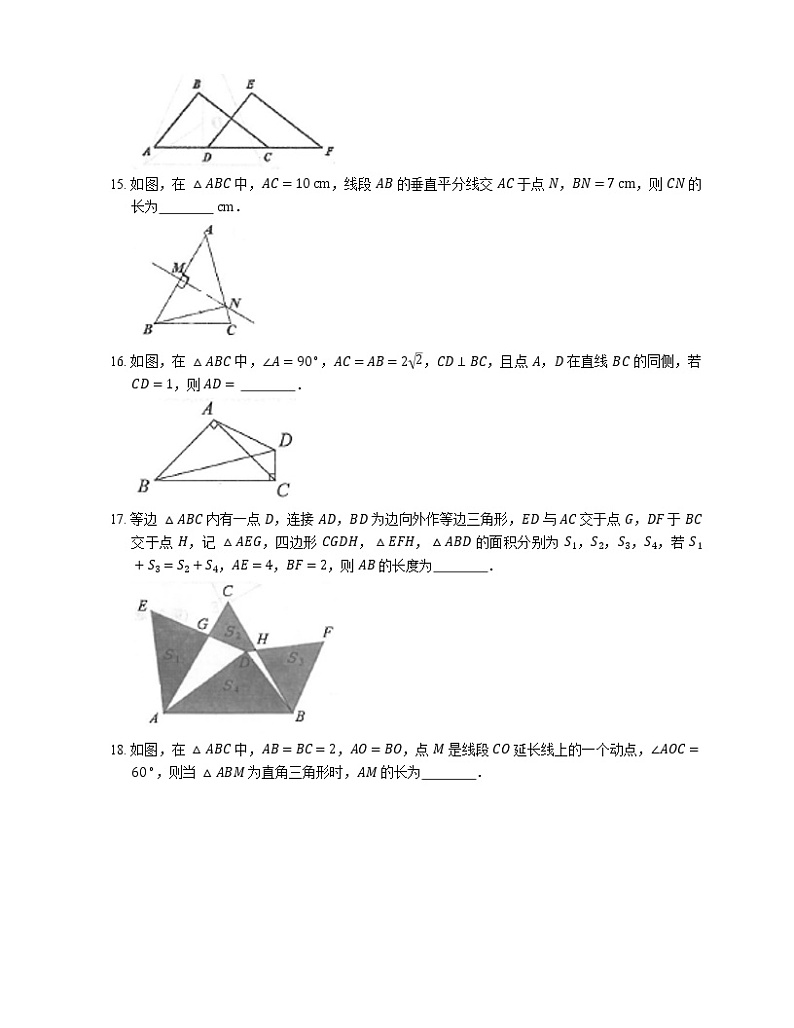
14. 如图,如图在 △ABC 和 △DEF 中,点 A,D,C,F 在同一直线上,AB=DE,AB∥DE,请添加一个条件,使 △ABC≌△DEF,这个添加的条件可以是 (只需写一个,不添加辅助线).
15. 如图,在 △ABC 中,AC=10 cm,线段 AB 的垂直平分线交 AC 于点 N,BN=7 cm,则 CN 的长为 cm.
16. 如图,在 △ABC 中,∠A=90∘,AC=AB=22,CD⊥BC,且点 A,D 在直线 BC 的同侧,若 CD=1,则 AD= .
17. 等边 △ABC 内有一点 D,连接 AD,BD 为边向外作等边三角形,ED 与 AC 交于点 G,DF 于 BC 交于点 H,记 △AEG,四边形 CGDH,△EFH,△ABD 的面积分别为 S1,S2,S3,S4,若 S1+S3=S2+S4,AE=4,BF=2,则 AB 的长度为 .
18. 如图,在 △ABC 中,AB=BC=2,AO=BO,点 M 是线段 CO 延长线上的一个动点,∠AOC=60∘,则当 △ABM 为直角三角形时,AM 的长为 .
三、解答题(共6小题;共78分)
19. 如图,已知 △ABC,按下列要求作图(第(1)、(2)小题用尺规作图,第(3)小题不限作图工具,保留作图痕迹).
(1)作 ∠B 的角平分线;
(2)作 AC 的中垂线;
(3)以 BC 边所在直线为对称轴,作 △ABC 的轴对称图形.
20. 如图,∠B=∠E=Rt∠,AB=AE,∠ACD=ADC.
求证:∠BAC=∠EAD.请补全证明过程,并在括号里写上理由.
证明:在 △ABC 中,
∵∠ACD=∠ADC,
∴AC= ,
在 Rt△ABC 和 Rt△AEC 中,
∵ =AD, =AE,
∴Rt△ABC≌Rt△AEC ,
∴∠BAC=∠EAD .
21. 如图,在 △ABC 中,AB=AC,∠BAC 和 ∠ACB 的平分线相交于点 D,ADC=125∘.求 ∠ACB 和 ∠BAC 的度数.
22. 如图,已知 AD 为 △ABC 的中线,延长 AD,分别过点 B,C 作 BE⊥AD,CF⊥AD.
(1)求证:△BED≌△CFD.
(2)若 ∠EAC=45∘,AF=4,DC=5,求 EF 的长.
23. 已知 △ABC,AB=AC,点 D 在线段 BC 上,点 E 在线段 AC 上,设 ∠BAD=α,∠CDE=β.
(1)如果 ∠B=60∘,α=20∘,β=10∘,那么 △ADE 是什么特殊三角形?请说明理由.
(2)猜想 α 与 β 之间有什么关系时,使得 AD=AE,并进行证明.
24. 如图,在等腰 △ABC 中,AB=CB,AD⊥BC,垂足为 D,已知 AD=3,CD=1.
(1)求 AC 与 AB 的长.
(2)点 P 是线段 AB 上的一点,
①当 AP 为何值时,△ADP 为等腰三角形.
②如点 P 关于直线 AC 的对称点为 E,关于直线 BC 的对称点为 F,连接 EF,若直线 EF 经过点 D 时,请直接写出 AP 的值.
答案
第一部分
1. B
2. D
3. B
4. C
5. C
6. A
7. B
8. C
9. A
10. D
第二部分
11. 70∘
12. 锐角
13. 如果a,b互为相反数,那么a+b=0
【解析】【分析】根据互逆命题的定义写出逆命题即可.
【解析】解:命题“如果a+b=0,那么a,b互为相反数”的逆命题为:
如果a,b互为相反数,那么a+b=0;
故答案为:如果a,b互为相反数,那么a+b=0.
【点评】本题考查的是命题与定理、互逆命题,掌握逆命题的确定方法是解题的关键.
14. ∠B=∠E
15. 3
16. 2
17. 25
18. 3,7 或 1
第三部分
19. 略
20. AD;等角对等边;AC;AB;HL;全等三角形对角相等
【解析】在 △ABC 中,
∵∠ACD=∠ADC,
∴AC=AD(等角对等边),
在 Rt△ABC 和 Rt△AEC 中,
∵AC=AD,AB=AE,
∴Rt△ABC≌Rt△AECHL,
∴∠BAC=∠EAD(全等三角形对角相等).
21. ∵∠ADC=125∘,
∴∠EAC+∠DCA=180∘−∠ADC=55∘.
∴∠ACB+∠BAC=110∘,∠B=180∘−∠ACB+∠BAC=70∘.
∵AB=AC,
∴∠B=∠ACB=70∘.
∴∠BAC=40∘.
22. (1) ∵AD 为中线,
∴BD=CD,
∴∠BED=∠CFD=90∘,
∴△BED≌△CFD.
(2) ∵∠A=45∘,AF=CF=4,DC=5,
∴DF=DC2−CF2=3,
∵△BED≌△CFD,
∴DF=DE,
∴EF=2DF=6.
23. (1) ∵AB=AC,∠B=60∘,
∴∠A=∠B=∠C=60∘.
∴∠DAE=60∘−∠α=40∘.
∴∠ADE=∠ADC−∠β=70∘,∠AED=∠C+∠β=70∘.
∵∠ADE=∠AED,
∴AD=AE.
∴△ADE 为等腰三角形.
(2) 要使 AD=AE,
∴∠ADE=∠AED,∠ADE=∠α+∠B−∠β,∠AED=∠C+∠β.
∵∠B=∠C,
∴∠ADE=∠AED,∠α+∠B−∠β=∠C+∠β.
∴∠α=2∠β.
24. (1) AC=32+12=10,
设 AB=CB=X,
DB=X−1,
AB2−DB2=AD2,
X2−X−12=9,
X=5,
∴AB=5.
(2) ①当 AP=AD 时,AP=3,
△ADP 为等腰三角形,
当 AP=DO 时,AP=52,
△ADP 为等腰三角形,
当 AD=DP 时,AP=185,
△ADP 为等腰三角形.
② AP=5或185.
2023-2024学年浙江省温州外国语学校九年级(上)期中数学试卷(含解析): 这是一份2023-2024学年浙江省温州外国语学校九年级(上)期中数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙江省温州市瓯海区部分学校2023-2024学年九年级上学期期中数学试卷: 这是一份浙江省温州市瓯海区部分学校2023-2024学年九年级上学期期中数学试卷,共4页。试卷主要包含了单选题,填空题,计算题等内容,欢迎下载使用。
2022-2023学年浙江省温州市瓯海区联盟学校七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年浙江省温州市瓯海区联盟学校七年级(下)期中数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












