2020-2021学年北京市东城区文汇中学八下期中数学试卷

这是一份2020-2021学年北京市东城区文汇中学八下期中数学试卷，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 若代数式 x−1 在实数范围内有意义，则 x 的取值范围是
A. x<1B. x≤1C. x>1D. x≥1

2. 下列四组线段中，可以构成直角三角形的是
A. 4，5，6B. 5，12，13C. 2，3，4D. 1，2，3

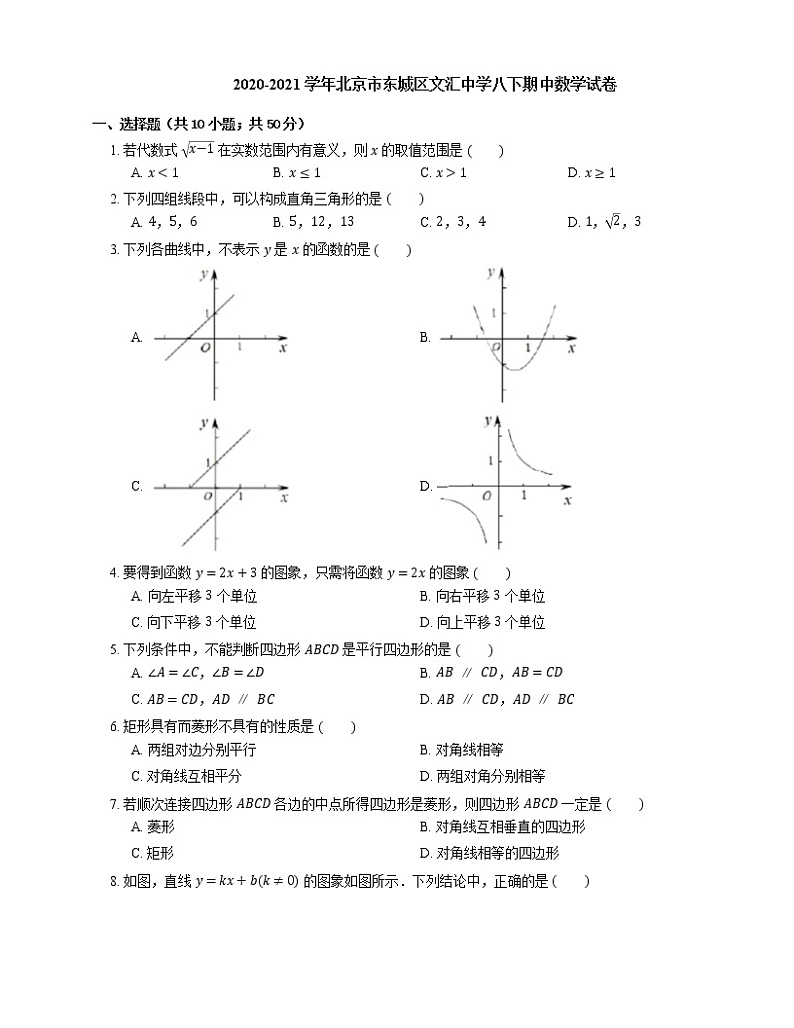
3. 下列各曲线中，不表示 y 是 x 的函数的是
A. B.
C. D.

4. 要得到函数 y=2x+3 的图象，只需将函数 y=2x 的图象
A. 向左平移 3 个单位B. 向右平移 3 个单位
C. 向下平移 3 个单位D. 向上平移 3 个单位

5. 下列条件中，不能判断四边形 ABCD 是平行四边形的是
A. ∠A=∠C，∠B=∠DB. AB∥CD，AB=CD
C. AB=CD，AD∥BCD. AB∥CD，AD∥BC

6. 矩形具有而菱形不具有的性质是
A. 两组对边分别平行B. 对角线相等
C. 对角线互相平分D. 两组对角分别相等

7. 若顺次连接四边形 ABCD 各边的中点所得四边形是菱形，则四边形 ABCD 一定是
A. 菱形B. 对角线互相垂直的四边形
C. 矩形D. 对角线相等的四边形

8. 如图，直线 y=kx+bk≠0 的图象如图所示．下列结论中，正确的是
A. k>0
B. 方程 kx+b=0 的解为 x=1；
C. b<0
D. 若点 A1,m，B3,n 在该直线图象上，则 m
9. 某校在“我运动，我快乐”的技能比赛培训活动中，在相同条件下，对甲、乙两名同学的“单手运球”项目进行了 5 次测试，测试成绩（单位：分）如下：根据下图判断正确的是
A. 甲成绩的平均分低于乙成绩的平均分
B. 甲成绩的中位数高于乙成绩的中位数
C. 甲成绩的众数高于乙成绩的众数
D. 甲成绩的方差低于乙成绩的方差

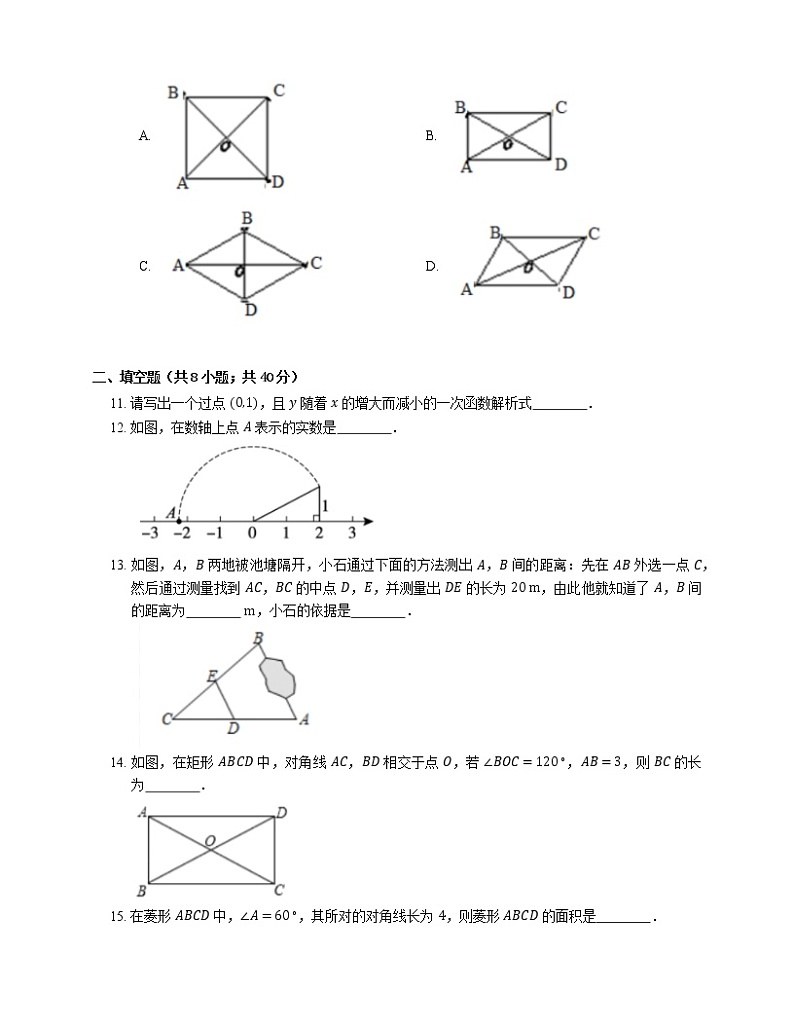
10. 已知某四边形的两条对角线相交于点 O．动点 P 从点 A 出发，沿四边形的边按 A→B→C 的路径匀速运动到点 C．设点 P 运动的时间为 x，线段 OP 的长为 y，表示 y 与 x 的函数关系的图象大致如图所示，则该四边形可能是
A. B.
C. D.

二、填空题（共8小题；共40分）
11. 请写出一个过点 0,1，且 y 随着 x 的增大而减小的一次函数解析式 ．

12. 如图，在数轴上点 A 表示的实数是 ．

13. 如图，A，B 两地被池塘隔开，小石通过下面的方法测出 A，B 间的距离：先在 AB 外选一点 C，然后通过测量找到 AC，BC 的中点 D，E，并测量出 DE 的长为 20 m，由此他就知道了 A，B 间的距离为 m，小石的依据是 ．

14. 如图，在矩形 ABCD 中，对角线 AC，BD 相交于点 O，若 ∠BOC=120∘，AB=3，则 BC 的长为 ．

15. 在菱形 ABCD 中，∠A=60∘，其所对的对角线长为 4，则菱形 ABCD 的面积是 ．

16. 在一次救灾捐款活动中，某班 50 名同学人人拿出自己的零花钱，有捐 5 元、 10 元、 20 元的，还有捐 50 元和 100 元的，统计图（如图）反映了不同捐款数的人数比例，那么该班同学捐款的众数和中位数分别是 元、 元．

17. 计算机可以帮助我们又快又准地画出函数的图象．用“几何画板”软件画出的函数 y=x2x−3 和 y=x−3 的图象如图所示．根据图象可知方程 x2x−3=x−3 的解的个数为 ；若 m，n 分别满足方程 x2x−3=1 和 x−3=1，则 m，n 的大小关系是 ．

18. 如图，点 A，B，E 在同一条直线上，正方形 ABCD，BEFG 的边长分别为 3，4，H 为线段 DF 的中点，则 BH= ．

三、解答题（共9小题；共117分）
19. 下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程．
已知：如图，在 Rt△ABC 中，∠ABC=90∘，O 为 AC 的中点．
求作：四边形 ABCD，使得四边形 ABCD 为矩形．
作法：①作射线 BO，在线段 BO 的延长线上取点 D，使得 DO=BO；
②连接 AD，CD，则四边形 ABCD 为矩形．
根据小丁设计的尺规作图过程．
（1）使用直尺和圆规，在图中补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：∴ 点 O 为 AC 的中点，
∴AO=CO．
又 ∵DO=BO，
∵ 四边形 ABCD 为平行四边形（ ）（填推理的依据）．
∵∠ABC=90∘，
∴ 平行四边形 ABCD 为矩形（ ）（填推理的依据）．

20. 已知：如图，在平行四边形 ABCD 中，点 E，F 分别在边 AD，BC 上，AE=CF．求证：BE=DF．

21. 在平面直角坐标系 xOy 中，已知一次函数 y=−12x+1 的图象与 x 轴交于点 A，与 y 轴交于点 B．
（1）求 A，B 两点的坐标；
（2）在给定的平面直角坐标系中画出该函数的图象；
（3）根据图象回答：当 y>0 时，x 的取值范围是 ．

22. 如图，长方形 ABCD 中，AB=8，BC=10，在边 CD 上取一点 E，将 △ADE 折叠后点 D 恰好落在 BC 边上的点 F 处．
（1）求 CE 的长；
（2）在（1）的条件下，BC 边上是否存在一点 P，使得 PA+PE 值最小?若存在，请求出最小值：若不存在，请说明理由．

23. 如图，在平面直角坐标系 xOy 中，直线 l 的表达式为 y=2x−6，点 A，B 的坐标分别为 1,0，0,2，直线 AB 与直线 l 相交于点 P．
（1）求直线 AB 的表达式；
（2）求点 P 的坐标；
（3）若直线 l 上存在一点 C，使得 △APC 的面积是 △APO 的面积的 2 倍，直接写出点 C 的坐标．

24. 在矩形 ABCD 中，连接 AC，AC 的垂直平分线交 AC 于点 O，分别交 AD，BC 于点 E，F，连接 CE 和 AF．
（1）求证：四边形 AECF 为菱形；
（2）若 AB=4，BC=8，求菱形 AECF 的面积．

25. 小云统计了自己所住小区 5 月 1 日至 30 日的厨余垃圾分出量（单位：千克），相关信息如下：
a．小云所住小区 5 月 1 日至 30 日的厨余垃圾分出量统计图：
b．小云所住小区 5 月 1 日至 30 日分时段的厨余垃圾分出量的平均数如下：
时段1日至10日11日至20日21日至30日平均数100170250
（1）该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为 （结果取整数）；
（2）已知该小区 4 月的厨余垃圾分出量的平均数为 60，则该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为 4 月的 倍（结果保留小数点后一位）；
（3）记该小区 5 月 1 日至 10 日的厨余垃圾分出量的方差为 s12，5 月 11 日至 20 日的厨余垃圾分出量的方差为 s22，5 月 21 日至 30 日的厨余垃圾分出量的方差为 s32．直接写出 s12，s22，s32 的大小关系．

26. 已知，点 E 在正方形 ABCD 的 AB 边上（不与点 A，B 重合），BD 是对角线，延长 AB 到点 F，使 BF=AE，过点 E 作 BD 的垂线，垂足为 M，连接 AM，CF．
（1）根据题意补全图形，并证明 MB=ME；
（2）①用等式表示线段 AM 与 CF 的数量关系，并证明；
②直接用等式表示线段 AM，BM，DM 之间的数量关系．

27. 平面直角坐标系中，对于点 Am,n 和点 Bm,nʹ，给出如下定义：
若 nʹ=n,m≥1−n,m<1，则称点 B 为点 A 的可变点，例如：点 1,4 的可变点的坐标是 1,4，点 −1,4 的可变点的坐标是 −1,−4．
（1）①点 3,1 的可变点的坐标是 ；
②在点 A−1,2，B2,−4 中有一个点是函数 y=2x 图象上某一个点的可变点，这个点是 ；（填“A”或“B”）
（2）若点 A 在函数 y=x+2−4≤x≤3 的图象上，求其可变点 B 的纵坐标 nʹ 的取值范围；
（3）若点 A 在函数 y=−x+4−1≤x≤a,a>−1 的图象上，其可变点 B 的纵坐标 nʹ 的取值范围是 −5≤nʹ≤3，直接写出 a 的取值范围．
答案
第一部分
1. D【解析】由题意得，x−1≥0，解得 x≥1．故选D．
2. B【解析】A、 ∵42+52≠62，∴ 该三角形不符合勾股定理的逆定理，故不可以构成直角三角形；
B、 ∵52+122=132，∴ 该三角形符合勾股定理的逆定理，故可以构成直角三角形；
C、 ∵22+32≠42，∴ 该三角形不符合勾股定理的逆定理，故不可以构成直角三角形；
D、 ∵12+22≠32，∴ 该三角形不符合勾股定理的逆定理，故不可以构成直角三角形．
3. C【解析】函数是指：在一个变化过程中，有两个变量 x，y，对于 x 的每一个取值，y 都有唯一确定的值与之对应．
选项C中，当 x 在 −1 到 1 之间时，过其中某点向 x 轴作垂线，该垂线与图形有两个交点，与函数的概念违背，故选项C中表示的不是函数．
选项A，B，D都满足函数概念．
4. D【解析】由题意得 x 值不变 y 增加 3 个单位，应向上平移 3 个单位．
5. C
【解析】平行四边形的判定方法有：①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③两组对角分别相等的四边形是平行四边形；④对角线互相平分的四边形是平行四边形；⑤一组对边平行且相等的四边形是平行四边形．
A、可以得到两组对边分别平行，根据：两组对边分别平行的四边形是平行四边形，判定四边形 ABCD 是平行四边形，故此选项不符合题意；
B、可以根据：一组对边平行且相等的四边形是平行四边形，判定四边形 ABCD 是平行四边形，故此选项不符合题意；
C、不能判定四边形 ABCD 是平行四边形，故此选项符合题意；
D、根据：两组对边分别平行的四边形是平行四边形，判定四边形 ABCD 是平行四边形，故此选项不符合题意．
6. B【解析】根据矩形与菱形的性质对各选项解析判断后利用排除法求解：
A.矩形与菱形的两组对边都分别平行，故本选项错误；
B.矩形的对角线相等，菱形的对角线不相等，故本选项正确；
C.矩形与菱形的对角线都互相平分，故本选项错误；
D.矩形与菱形的两组对角都分别相等，故本选项错误．
7. D【解析】∵E，F，G，H 分别是边 AD，DC，CB，AB 的中点，
∴EH=12AC，EH∥AC，FG=12AC，FG∥AC，EF=12BD，
∴EH∥FG，EF=FG，
∴ 四边形 EFGH 是平行四边形，
假设 AC=BD，
∵EH=12AC，EF=12BD，
则 EF=EH，
∴ 平行四边形 EFGH 是菱形，
即只有具备 AC=BD 即可推出四边形是菱形．
8. B【解析】由图象得：k<0，b>0，
∴ A，C 都错误；
∵ 图象与 x 轴交于点 1,0，
∴ 方程 kx+b=0 的解为 x=1，故B正确；
∵k<0，
∴y 随着 x 的增大而减小，由 1<3 得 m>n，故D错误，
故选：B．
9. D【解析】甲的平均数 =157+8+8+9+8=8（分），
乙的平均数 =1510+7+9+4+10=8（分），
所以A选项错误；
甲的中位数是 8 分，乙的中位数是 9 分，故B选项错误；
甲的众数是 8 分，乙的众数是 10 分，故C选项错误；
甲的方差 =157−82+3×8−82+9−82=25，
乙的方差 =152×10−82+7−82+9−82+4−82=265，
故D选项正确．
10. D
【解析】A，C选项 A→B→C 路线都关于对角线 BD 对称，因而函数图象应具有对称性，故A，C错误，对于选项B点 P 从 A 到 B 过程中 OP 的长也存在对称性，则图象前半段也应该具有对称特征，故B错误．
第二部分
11. y=−x+1
【解析】设该一次函数的解析式为 y=kx+b，
∵y 随着 x 的增大而减小，
∴k<0，
取 k=−1，
∵ 点 0,1 在一次函数图象上，
∴b=1，
故答案为 y=−x+1．
12. −5
【解析】由题意得，
OA=12+22=5，
∵ 点 A 在原点的左边，
∴ 点 A 表示的实数是 −5．
13. 40，三角形中位线定理
【解析】因为点 D，E 是 AC，BC 的中点，
所以 AB=2DE=40m，
小石的依据是三角形中位线定理．
14. 33
【解析】∵∠BOC=120∘，
∴∠AOB=60∘，
∵ 四边形 ABCD 是矩形，
∴∠ABC=90∘，AC=BD，AO=OC，BO=DO，
∴AO=BO，
∴△AOB 是等边三角形，
∴AB=AO=BO，
∵AB=3，
∴AO=3，
∴AC=2AO=6，
由勾股定理得：BC=AC2−AB2=62−32=33．
15. 83
【解析】如图所示：
因为在菱形 ABCD 中，∠BAD=60∘，其所对的对角线长为 4，
所以可得 AD=AB，故 △ABD 是等边三角形，
则 AB=AD=4，
故 BO=DO=2，
则 AO=42−22=23，
故 AC=43，
则菱形 ABCD 的面积是：12×4×43=83．
16. 20，20
【解析】由扇形图知，捐款 5 元的人数为 50×8%=4（名），捐款 10 元的人数为 50×20%=10（名），
捐款 20 元的人数为 50×44%=22（名），捐款 50 元的人数为 50×16%=8（名），
捐款 100 元的人数为 50×12%=6（名），
所以这组数据的众数为 20 元，中位数为 20+202=20（元）．
17. 3，m【解析】由图象可知，函数 y=x2x−3 和 y=x−3 的图象共有 3 个交点，
则方程 x2x−3=x−3 的解的个数为 3；
由题意得：点 m,1 在函数 y=x2x−3 的图象上，点 n,1 在函数 y=x−3 的图象上，
如图，
由图象可知，m18. 522
【解析】连接 BD，BF，
∵ 四边形 ABCD 和四边形 BEFG 是正方形，
∴∠DBC=∠GBF=45∘，BD=32+32=32，BF=42+42=42，
∴∠DBF=90∘，
∴DF=BD2+BF2=322+422=52，
∵H 为线段 DF 的中点，
∴BH=522．
第三部分
19. （1） 如图，矩形 ABCD 即为所求．
（2） 对角线互相平分的四边形是平行四边形；有一个角是直角的平行四边形是矩形．
【解析】理由：∵ 点 O 为 AC 的中点，
∴AO=CO．
又 ∵DO=BO，
∴ 四边形 ABCD 为平行四边形（对角线互相平分的四边形是平行四边形），
∵∠ABC=90∘，
∴ 平行四边形 ABCD 为矩形（有一个角是直角的平行四边形是矩形）．
20. ∵ 四边形 ABCD 是平行四边形，
∴AD=BC，AD∥BC，
∵AE=CF，
∴DE=BF，
又 ∵DE∥BF，
∴ 四边形 BEDF 是平行四边形，
∴BE=DF．
21. （1） 令 y=0，则 x=2，令 x=0，则 y=1，
所以点 A 的坐标为 2,0，点 B 的坐标为 0,1．
（2） 如图：
（3） x<2
【解析】当 y>0 时，x 的取值范围是 x<2，故答案为 x<2．
22. （1） 长方形 ABCD 中，AB=8，BC=10，
所以 ∠B=∠BCD=90∘，CD=AB=8，AD=BC=10，
由折叠知，EF=DE，AF=AD=8，
在 Rt△ABF 中，根据勾股定理得，BF=AF2−AB2=6，
所以 CF=BC−BF=4，
设 CE=x，则 EF=DE=CD−CE=8−x，
在 Rt△ECF 中，根据勾股定理得，CF2+CE2=EF2，
所以 16+x2=8−x2，
所以 x=3，
所以 CE=3．
（2） 如图，延长 EC 至 Eʹ 使 CEʹ=CE=3，连接 AEʹ 交 BC 于 P，此时，PA+PE 最小，最小值为 AEʹ，
因为 CD=8，
所以 DEʹ=CD+CEʹ=8+3=11，
在 Rt△ADEʹ 中，根据勾股定理得，AEʹ=AD2+DEʹ2=221．
23. （1） 设直线 AB 的表达式为 y=kx+b．
由点 A，B 的坐标分别为 1,0，0,2，
可知 k+b=0,b=2.
解得 k=−2,b=2.
∴ 直线 AB 的表达式为 y=−2x+2．
（2） 由题意，
得 y=−2x+2,y=2x−6.
解得 x=2,y=−2.
所以点 P 的坐标为 2,−2．
（3） 3,0，1,−4．
24. （1） ∵EF 是 AC 的垂直平分线，
∴AO=OC，∠AOE=∠COF=90∘，
∵ 四边形 ABCD 是矩形，
∴AD∥BC，
∴∠EAO=∠FCO，
在 △AEO 和 △CFO 中，
∠EAO=∠FCO,AO=CO,∠AOE=∠COF,
∴△AEO≌△CFOASA；
∴OE=OF，
又 ∵OA=OC，
∴ 四边形 AECF 是平行四边形，
又 ∵EF⊥AC，
∴ 平行四边形 AECF 是菱形．
（2） 设 AF=x，
∵EF 是 AC 的垂直平分线，
∴AF=CF=x，BF=8−x，
在 Rt△ABF 中，由勾股定理得：
AB2+BF2=AF2，42+8−x2=x2，
解得 x=5．
∴AF=5，
∴ 菱形 AECF 的周长为 20．
25. （1） 173
【解析】该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为 100×10+170×10+250×1030≈173（千克）．
（2） 2.9
【解析】该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为 4 月的 17360≈2.9（倍）．
（3） s12>s22>s32
【解析】由小云所住小区 5 月 1 日至 30 日的厨余垃圾分出量统计图知，第 1 个 10 天的分出量最分散、第 3 个 10 天分出量最为集中，
∴s12>s22>s32．
26. （1） 如图所示：
∵ 四边形 ABCD 是正方形，BD 是对角线，
∴∠ABD=45∘，
∵BM⊥BD，
∴△BEM 是等腰直角三角形，
∴MB=ME．
（2） ①如图所示，连接 CM，FM，
∵△BEM 是等腰直角三角形，
∴MB=ME，∠ABM=∠BEM=45∘，
∴∠AEM=∠FBM=135∘，
又 ∵AE=FB，
∴△AEM≌△FBMSAS，
∴AM=FM，
∵AE=BF，
∴EF=BC=AB，
∴△MEF≌△MBCSAS，
∴∠EMF=∠BMC，FM=MC，
∴∠FMC=90∘，
∴△FCM 是等腰直角三角形，
∴FC=2MF=2AM，
即 2AM=FC；
② DM2+BM2=2AM2．
【解析】② DM2+BM2=2AM2，理由如下：
如图，连接 DE，
∵AE=BF，
∴AE+BE=BF+BE=EF，
又 ∵DC∥AB 且 DC=AB，
∴DC=EF，DC∥EF，
∴ 四边形 CDEF 是平行四边形，
∴DE=CF，
∵CF=2MF，MF=AM，
∴DE=2AM，
又 BM=EM，∠DME=90∘，
∴DM2+EM2=DE2，
则 DM2+BM2=2AM2．
27. （1） ① 3,1；② A
【解析】①由定义可知，3>1，
所以点 3,1 的可变点的坐标是 3,1；
②点 A−1,2 的可变点为 −1,−2，在函数 y=2x 图象上，B2,−4 的可变点为 2,−4，不在函数 y=2x 图象上．故这个点为点 A．
（2） 若点 A 在函数 y=x+2−4≤x≤3 的图象上，设 Ax,x+2，
当 1≤x≤3 时，3≤x+2≤5，即 3≤nʹ≤5，
当 −4≤x<1 时，−3≤−x+2≤2，即 −3≤nʹ≤2．
所以纵坐标 nʹ 的取值范围为 3≤nʹ≤5 或 −3≤nʹ≤2．
（3） 7【解析】依题意，y=−x+4−1≤x≤a,a>−1 图象上的点 A 的可变点 B 必在函数 nʹ=−x+4,x≥1x−4,x<1 的图象上，当 x=1 时，nʹ 取最大值，nʹ=−1+4=3，当 nʹ=−5 时，x−4=−5 或 −x+4=−5，
所以 x=−1 或 x=9，
当 nʹ=−3 时，−x+4=−3，
所以 x=7．
因为 −5≤nʹ≤3，
所以由图象可知，a 的取值范围是：7