2020-2021学年北京市丰台区第十二中学八下期中数学试卷

这是一份2020-2021学年北京市丰台区第十二中学八下期中数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. △ABC 中，∠A，∠B，∠C 的对边分别是 a，b，c，下列命题中的假命题是
A. 如果 ∠C−∠B=∠A，则 △ABC 是直角三角形
B. 如果 c2=b2−a2，则 △ABC 是直角三角形，且 ∠C=90∘
C. 如果 c+ac−a=b2，则 △ABC 是直角三角形
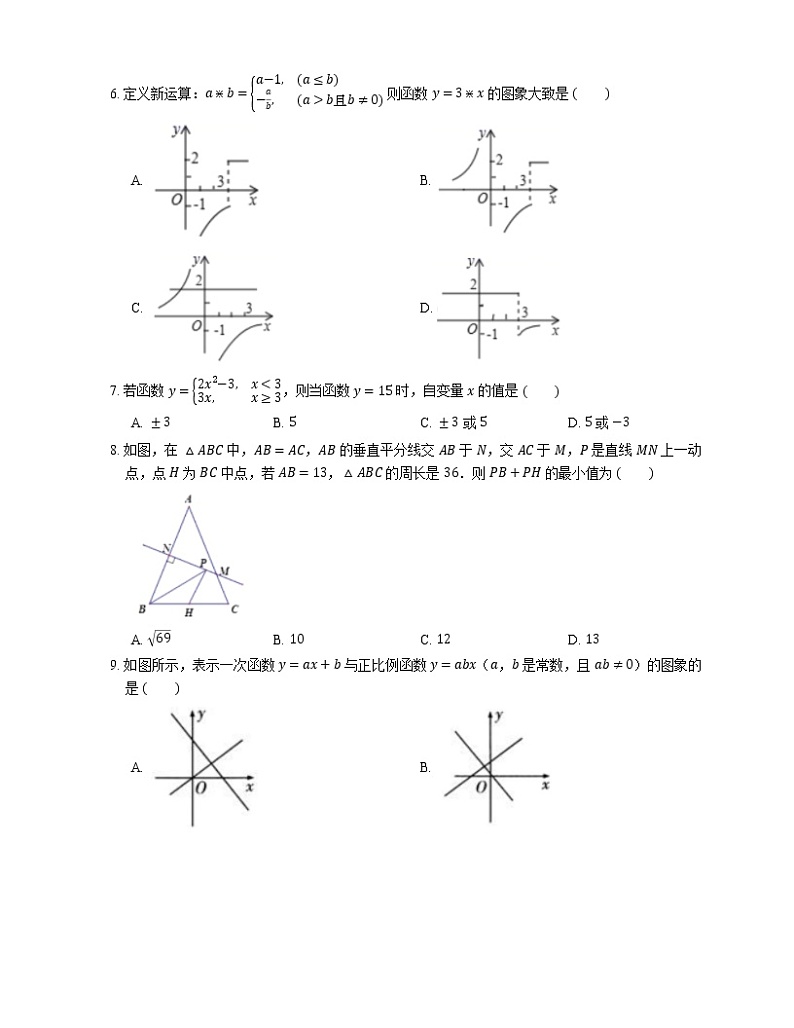
D. 如果 ∠A:∠B:∠C=5:2:3，则 △ABC 是直角三角形

2. 如图，菱形 ABCD 对角线 AC 与 BD 交于点 O，点 E 是 DC 边上的中点，连接 OE，OE=5，BD=12，则菱形的面积为
A. 96B. 48C. 192D. 24

3. 若点 Am,n 在函数 y=23x+b 的图象上，且 2m−3n>6，则 b 的取值范围为
A. b>2B. b>−2C. b<2D. b<−2

4. 如图，在 △ABC 中，CD⊥AB 于点 D，E，F 分别为 AC，BC 的中点，AB=10，BC=8，DE=4.5，则 △DEF 的周长是
A. 9.5B. 12.5C. 13.5D. 14.5

5. 如图，函数 y=2x 和 y=ax+4 的图象相交于点 Am,3，则不等式 2xA. x<32B. x>32C. x<3D. x>3

6. 定义新运算：a⋇b=a−1,a≤b−ab,a>b且b≠0 则函数 y=3⋇x 的图象大致是
A. B.
C. D.

7. 若函数 y=2x2−3,x<33x,x≥3，则当函数 y=15 时，自变量 x 的值是
A. ±3B. 5C. ±3 或 5D. 5 或 −3

8. 如图，在 △ABC 中，AB=AC，AB 的垂直平分线交 AB 于 N，交 AC 于 M，P 是直线 MN 上一动点，点 H 为 BC 中点，若 AB=13，△ABC 的周长是 36．则 PB+PH 的最小值为
A. 69B. 10C. 12D. 13

9. 如图所示，表示一次函数 y=ax+b 与正比例函数 y=abx（a，b 是常数，且 ab≠0）的图象的是
A. B.
C. D.

10. 如图，已知正方形 ABCD 的边长为 4，P 是对角线 BD 上一点，PE⊥BC 于点 E，PF⊥CD 于点 F，连接 AP，EF．给出下列结论：
① PD=2EC；
②四边形 PECF 的周长为 8；
③ AP=EF；
④ EF 的最小值为 22；
⑤ PB2+PD2=2PA2；
⑥ AP⊥EF．
其中正确结论有几个
A. 3B. 4C. 5D. 6

二、填空题（共10小题；共50分）
11. 将直线 y=−x 向上平移 p 个单位后，经过点 m,n，若 m+n=3，则 p= ．

12. 函数 y=2−x+1x−1 中自变量 x 的取值范围是 ．

13. 已知一次函数 y=kx+b 的图象如图，当 x<0 时，y 的取值范围是 ．

14. 如图，平行四边形 ABCD 中，AE 平分 ∠BAD，若 CE=4 cm，AD=5 cm，则平行四边形 ABCD 的周长是 ．

15. 如图，平面直角坐标系中，△ABC 的顶点坐标分别是 A2,2，B6,2，C4,4，当直线 y=12x+b 与 △ABC 有交点时，b 的取值范围是 ．

16. 如下图，四边形 OABC 是矩形，A2,1，B0,5，点 C 在第二象限，则点 C 的坐标是 ．

17. 如图，在矩形 ABCD 中，AB=6，对角线 AC，BD 相交于点 O，AE 垂直平分 BO 于点 E，则 AD 的长为 ．

18. 如图，正方形 ABCD 和正方形 EFCG 的边长分别为 3 和 1，点 F，G 分别在边 BC，CD 上，P 为 AE 的中点，连接 PG，则 PG 的长为 ．

19. 在A、B两地之间有汽车站C（C在直线AB上），甲车由A地驶往C站，乙车由B地驶往A地，两车同时出发，匀速行驶．甲、乙两车离C站的路程 y1，y2（千米）与行驶时间 x（小时）之间的函数图象如图所示，则下列结论：①A、B两地相距 440 千米；②甲车的平均速度是 60 千米/时；③乙车行驶 11 小时后到达A地；④两车行驶 4.4 小时后相遇，其中正确的结论有是 （填序号）．

20. 如图所示，是由北京国际数学家大会的会徽演化而成的图案，其主体部分是由一连串的等腰直角三角形依次连接而成，其中 ∠MA1A2=∠MA2A3⋯=∠MAnAn+1=90∘，（n 为正整数），若 M 点的坐标是 −1,2，A1 的坐标是 0,2，则 A22 的坐标为 ．

三、解答题（共10小题；共130分）
21. 已知一次函数 y=kx+b，当 −3≤x≤1 时，对应 y 的取值范围是 1≤y≤9，求该函数的解析式．

22. 如图，直线 l1:y=2x−3 与 x 轴交于点 A，直线 l2 经过点 B4,0，C0,2，与 l1 交于点 D．
（1）求直线 l2 的解析式；
（2）求 △ABD 的面积．

23. 如图，在 △ABC 中，∠BAC=90∘，∠B=45∘，BC=10 cm，过点 A 作 AD∥BC，且点 D 在点 A 的右侧，点 P 从点 A 出发沿射线 AD 方向以每秒 1 cm 的速度运动，同时点 Q 从点 C 出发沿射线 CB 方向以每秒 2 cm 的速度运动，在线段 QC 上取点 E，使得 QE=2 cm，连接 PE，设点 P 的运动时间为 t 秒．
（1）① CE= （用含 t 的式子表示）
②若 PE⊥BC，求 BQ 的长；
（2）请问 t 为何值时，使以 A，B，E，P 为顶点的四边形为平行四边形?直接写出 t 的值．

24. 某市为节约水资源，制定了新的居民用水收费标准，按照新标准，用户每月缴纳的水费 Y（元）与每月用水量 xm3 之间的关系如图所示．
（1）求 y 关于 x 的函数表达式；
（2）若某用户二、三月份共用水 40 m3（二月份用水量不超过 25m3），缴纳水费 79.8 元，则该用户二、三月份的用水量各是多少?

25. 如图，在长方形 ABCD 中，DC=5 cm，在 DC 上存在一点 E，沿直线 AE 把 △AED 折叠，使点 D 恰好落在 BC 边上，设此点为 F，若 △ABF 的面积为 30 cm2，求折叠 △AED 的面积．

26. 如图，在平面直角坐标系中，一次函数 y=kx+b 的图象与 x 轴交点为 A−3,0，与 y 轴交点为 B，且与正比例函数 y=43x 的图象交于点 Cm,4．
（1）求 m 的值及一次函数 y=kx+b 的表达式；
（2）若点 P 是直线 y=43x 上一点，且 △BPC 的面积为 6，请求出点 P 的坐标．

27. 如图，已知一次函数 y=kx+b 的图象与反比例函数 y=mx 的图象交于 A，B 两点，A 点的坐标是 −2,1，B 点的坐标是 1,n．
（1）求出两个函数解析式；
（2）在 x 轴正半轴上是否存在点 P，使 △ABP 为等腰三角形?若存在，求 P 点坐标；若不存在，请说明理由．
（3）直接写出满足 0
28. 有这样一个问题：探究函数 y=1x2+x 的图象与性质．
小菲根据学习函数的经验，对函数 y=1x2+x 的图象与性质进行了探究．
下面是小菲的探究过程，请补充完整：
（1）函数 y=1x2+x 的自变量 x 的取值范围是 ．
（2）下表是 y 与 x 的几组对应值．
x⋯−3−2−1−23−122312123⋯y⋯−269−74m191272351292294289⋯
表中 m 的值为 ．
（3）如下图，在平面直角坐标系 xOy 中，描出补全后的表中各组对应值所对应的点，并画出该函数的图象；
（4）根据画出的函数图象，写出：
① x=1.5 时，对应的函数值 y 约为 （结果保留一位小数）；
②该函数的一条性质： ．

29. 如图 1，在四边形 ABCD 的边 BC 的延长线上取一点 E，在直线 BC 的同侧作一个 CE 为底的等腰 △CEF，且满足 ∠B+∠F=180∘，称 △CEF 为四边形 ABCD 的“伴随三角形”．
（1）如图 1，若 △CEF 是正方形 ABCD 的“伴随三角形”．
①连接 AC，则 ∠ACF= ∘；
②若 CE=2BC，连接 AE 交 CF 于 H，求证：H 是 CF 的中点．
（2）如图 2，若 △CEF 是菱形 ABCD 的“伴随三角形”，∠B=60∘，M 是线段 AE 的中点，连接 DM，FM，猜想并证明 DM 与 FM 的位置关系与数量关系．

30. 在平面直角坐标系 xOy 中，如果点 A，点 C 为某个菱形的一组对角的顶点，且点 A，C 在直线 y=x 上，那么称该菱形为点 A，C 的“极好菱形”．下图为点 A，C 的“极好菱形”的一个示意图．已知点 M 的坐标为 1,1，点 P 的坐标为 3,3．
（1）点 E2,4，F1,3，G4,0，H3,2 中，能够成为点 M，P 的“极好菱形”的顶点的是 ；
（2）如果四边形 MNPQ 是点 M，P 的“极好菱形”．
①当点 N 的坐标为 52,32 时，求四边形 MNPQ 的面积；
②当四边形 MNPQ 的面积为 12，且与直线 y=x+b 有公共点时，求出 b 的取值范围．
答案
第一部分
1. B
2. A【解析】∵ 四边形 ABCD 是菱形，
∴AC⊥BD，OD=12BD=6，OC=12AC，
∴CD=2OE=10，
∴OC=CD2−OD2=102−62=8，
∴AC=2OC=16，
∴ 菱形的面积为：12AC⋅BD=12×16×12=96．
故选A．
3. D
4. C
5. A
6. B
7. D
8. C
9. C
10. D
第二部分
11. 3
12. x≤2 且 x≠1
13. y<−2
14. 28 cm
15. −1≤b≤2
16. −2,4
17. 63
18. 5
19. ①②③④
20. −1−210,2−210
第三部分
21. ∵ 一次函数 y=kx+b，当 −3≤x≤1 时，1≤y≤9，
∴ ①当 k<0 时，y 随 x 的增大而减小，
即当 x=−3 时，y=9；当 x=1 时，y=1，
∴−3k+b=9,k+b=1.
解得 k=−2,b=3.
∴y=−2x+3．
②当 k>0 时，y 随 x 的增大而增大，
即当 x=−3 时，y=1；当 x=1 时，y=9，
∴−3k+b=1,k+b=9.
解得 k=2,b=7.
∴y=2x+7．
22. （1） 设直线 l2 的解析式是 y=kx+b，
则 4k+b=0,0+b=2,
解得：k=−12,b=2.
则直线 l2 的解析式是 y=−12x+2；
（2） 在 y=2x−3 中，令 y=0，则 2x−3=0，解得 x=32，
则 A 的坐标是 32,0．
根据题意得：y=2x−3,y=−12x+2,
解得：x=2,y=1.
D2,1，
AB=4−32=52，
则 S△ABD=12×52×1=54．
23. （1） ① 2t−2t≥1；
②作 AM⊥BC 于 M，交 AC 于点 N，如图所示，
∵∠BAC=90∘，∠B=45∘，
∴∠C=45∘=∠B，
∴AB=AC，
∴BM=CM，
∴AM=12BC=5 cm，
∵AD∥BC，
∴∠PAC=∠C=45∘，
∵PE⊥BC，
∴PE=AM=5，PE⊥AD，
∴△APN 和 △CEN 是等腰直角三角形，
∴PN=AP=t，CE=NE=5−t，
∵CE=CQ−QE=2t−2，
∴5−t=2t−2，
∴t=73，
∴BQ=BC−CQ=10−2×73=163；
【解析】① 2t−2t≥1；
理由：由运动知，CQ=2t，
∵ 在线段 QC 上取点 E，使得 QE=2 cm，则 CQ≥2 cm，t≥1 秒，
∴CE=CQ−EQ=2t−2t≥1．
（2） t=4秒或12秒
【解析】存在，t=4或12 s；理由如下：
（ⅰ）当点 Q，E 在线段 BC 上时，
若以 A，B，E，P 为顶点的四边形为平行四边形，
则 AP=BE，
∴t=10−2t+2，
解得：t=4，
（ⅱ）当点 Q，E 在线段 CB 的延长线上时，
若以 A，B，E，P 为顶点的四边形为平行四边形，
则 AP=BE，
t=2t−2−10，
解得：t=12，
∴t=4秒或12秒 时，使以 A，B，E，P 为顶点的四边形为平行四边形．
24. （1） 当 0≤x≤15 时，设 y 与 x 的函数关系式为 y=kx，
15k=27，得 k=1.8，
即当 0≤x≤15 时，y 与 x 的函数关系式为 y=1.8x，
当 x>15 时，设 y 与 x 的函数关系式为 y=ax+b，
15a+b=27,20a+b=39,
解得 a=2.4,b=−9,
即当 x>15 时，y 与 x 的函数关系式为 y=2.4x−9，
由上可得，y 与 x 的函数关系式为 y=1.8x,0≤x≤152.4x−9.x>15
（2） 设二月份的用水量是 x m3，
当 15解得，x 无解，
当 0解得，x=12，
∴40−x=28，
答：该用户二、三月份的用水量各是 12 m3，28 m3．
25. 由折叠的对称性，得 AD=AF，DE=EF．
由 S△ABF=12BF⋅AB=30，AB=5，
得 BF=12．
在 Rt△ABF 中，由勾股定理，得
AF=AB2+BF2=13．
所以 AD=13．
设 DE=x，则 EC=5−x，EF=x，FC=1，
在 Rt△ECF 中，EC2+FC2=EF2，
即 5−x2+12=x2．
解得 x=135．
故 S△ADE=12AD⋅DE=12×13×135=16.9cm2．
26. （1） ∵ 点 Cm,4 在正比例函数 y=43x 的图象上，
∴4=43m，
解得 m=3，即点 C 坐标为 3,4，
∵ 一次函数 y=kx+b 经过 A−3,0，点 C3,4，
∴ 0=−3k+b,4=3k+b, 解得：k=23,b=2,
∴ 一次函数 y=kx+b 的表达式为 y=23x+2；
（2） 点 P 的坐标为 −3,−4 或 9,12．
27. （1） ∵ 反比例函数 y=mx 的图象过点 A−2,1，B1,n，
∴m=−2×1=−2，m=1×n，
∴n=−2，
∴y=−2x，
∴B1,−2，
∵ 一次函数 y=kx+b 的图象过 A，B 两点，
∴k+b=−2,−2k+b=1,
解得 k=−1，b=−1；
∴ 一次函数的解析式为 y=−x−1．
（2） AB=32，AP=AB=32，P−2+17,0，
BP=AB=32，P1+14,0，
∴P−2+17,0 或 P1+14,0．
（3） ∵C−1,0，A−2,1，
∴028. （1） x≠0
（2） m=0
（3） 图象略
（4） ① 1.9 至 2.0
②答案不唯一，如 x<0 时，y 随 x 的增大而增大
29. （1） ① 90
②设 BC=a，则 CE=2a，
∵△CEF 是正方形 ABCD 的“伴随三角形”，
∴∠B=90∘，△CEF 是等腰直角三角形，
∴AC=2a，EF=2a，
∴AC=EF，
在 △ACH 和 △EFH 中，
∠AHC=∠EHF,∠ACF=∠F,AC=EF,
∴△ACH≌△EFH，
∴CH=FH，即 H 是 CF 的中点．
（2） DM=3FM，FM⊥DM．
理由如下：如图，延长 DM 交 CE 于点 P，连接 DF，FP，
∵ 四边形 ABCD 是菱形，
∴AB=BC=CD=AD，AB∥CD，AD∥BC，
∴∠B=∠DCP=60∘，∠DAM=∠PEM，
∵ 若 △CEF 是菱形 ABCD 的“伴随三角形”，∠B=60∘，
∴∠CFE+∠B=180∘，
∴∠CFE=120∘，且 △CEF 是等腰三角形，
∴∠ECF=30∘=∠FEC，CF=EF，
∴∠DCF=30∘，
∵∠DAM=∠PEM，AM=ME，∠AMD=∠PME，
∴△ADM≌△EPMASA，
∴AD=PE，DM=MP，
∴CD=PE，且 CF=EF，∠DCF=∠FEC=30∘，
∴△CDF≌△EPFSAS，
∴DF=PF，∠DFC=∠PFE，
∵∠PFE+∠CFP=∠CFE=120∘，
∴∠DFC+∠CFP=120∘=∠DFP，且 DF=FP，DM=PM，
∴FM⊥DM，∠FDM=30∘，
∴DM=3FM．
30. （1） F，G
（2） ① ∵ 四边形 MNPQ 是菱形，
∴S四边形MNPQ=2⋅22÷2=2．
②如图，
∵ 点 M 的坐标为 1,1，点 P 的坐标为 3,3，
∴PM=22，可得 Q−1,5，N5,−1，
当直线 y=x+b 经过点 Q−1,5 时，b=6，
当 y=x+b 经过时 N5,−1 时，b=−6，
∴ 当四边形 MNPQ 与直线 y=x+b 有公共点时，b 的取值范围是 −6≤b≤6．