


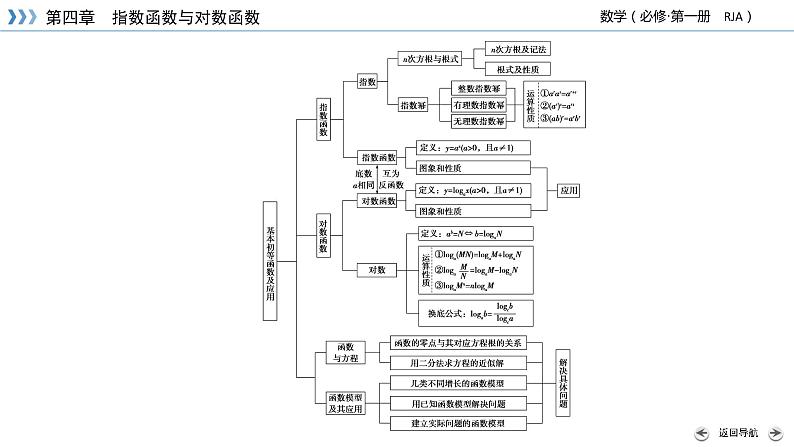



人教A版 (2019)必修 第一册第四章 指数函数与对数函数本章综合与测试公开课课件ppt
展开注:指数函数y=ax(a>0且a≠1)与对数函数y=lgax(a>0且a≠1)互为反函数,它们的图象关于直线y=x对称(如图所示).
4.函数的零点(1)函数零点的定义对于函数y=f(x)(x∈D),把使f(x)=0的实数x叫做函数y=f(x)(x∈D)的零点.(2)几个等价关系方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.
(3)函数零点的判定如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
5.给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:(1)确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε.(2)求区间(a,b)的中点c.(3)计算f(c)①若f(c)=0,则c就是函数的零点;②若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c));③若f(c)·f(b)<0,则令a=c(此时零点x0∈(c,b)).(4)判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b),否则重复(2)~(4).
6.指数函数、对数函数和幂函数的增长趋势比较
选取上述三个增长函数模型时,应注意:(1)当描述增长速度变化很快时,常常选用指数函数模型.(2)当要求不断增长,但又不会增长过快,也不会增长到很大时,常常选用对数函数模型.(3)幂函数模型y=xn(n>0)可以描述增长幅度不同的变化,当n值较小(n≤1)时,增长较慢;当n值较大(n>1)时,增长较快.
7.建立函数模型解决实际问题的基本思路
[归纳提升] 指数、对数的运算应遵循的原则(1)指数的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算;其次若出现分式则要注意分子、分母因式分解以达到约分的目的.(2)对数的运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的运算性质并结合对数恒等式、换底公式是对数计算、化简、证明的常用技巧.
函数y=2lg4(1-x)的图象大致是( )
[解析] 方法一:当x=0时,y=0,故可排除选项A,由1-x>0,得x<1,即函数的定义域为(-∞,1),排除选项B,又易知函数在其定义域上是减函数.方法二:函数y=2lg4(1-x)的图象可认为是由y=lg4x的图象经过如下步骤变换得到的:(1)函数y=lg4x的图象上所有点的横坐标不变.纵坐标变为原来的2倍,得到函数y=2lg4x的图象;(2)把函数y=2lg4x关于y轴对称得到函数y=2lg4(-x)的图象;(3)把函数y=2lg4(-x)的图象向右平移1个单位,即可得到y=2lg4(1-x)的图象.[归纳提升] 弄清所给函数与基本函数的关系,恰当选择平移、对称等变换方法,由基本函数图象变换得到函数图象.
讨论函数f(x)=x2-2|x|-1-a(a∈R)的零点的个数.
当a在R上取值时,函数h(x)的图象是一系列垂直于y轴的直线.①当a<-2时,g(x)的图象与直线y=a无交点,方程x2-2|x|-1=a无实根,即函数f(x)无零点;②当a=-2,或a>-1时,g(x)的图象与直线y=a的图象有两个交点,即函数f(x)有两个零点;③当-2
函数f(x)=lga(1-x)+lga(x+3)(0
2016年冬季,我国大部分地区遭遇雾霾天气,给人们的健康、交通安全等带来了严重影响.经研究,发现工业废气等污染物排放是雾霾形成和持续的重要因素,污染治理刻不容缓.为此,某工厂新购置并安装了先进的废气处理设备,使产生的废气经过过滤后排放,以降低对空气的污染.已知过滤过程中废气的污染物数量P(单位:mg/L)与过滤时间t(单位:小时)间的关系为P=P0e-kt(P0,k均为非零常数,e为自然对数的底数),其中P0为t=0时的污染物数量.若经过5小时过滤后还剩余90%的污染物.
(1)求常数k的值;(2)试计算污染物减少到40%至少需要多少时间(精确到1小时,参考数据:ln 0.2≈-1.61,ln 0.3≈-1.20,ln 0.4≈-0.92,ln 0.5≈-0.69,ln 0.9≈-0.11).
[归纳提升] 建模的三个原则(1)简化原则:建立模型,要对原型进行一定的简化,抓主要因素、主变量,尽量建立较低阶、较简便的模型.(2)可推演原则:建立的模型一定要有意义,既能对其进行理论分析,又能计算和推理,且能推演出正确结果.(3)反映性原则:建立的模型必须真实地反映原型的特征和关系,即应与原型具有“相似性”,所得模型的解应具有说明现实问题的功能,能回到具体研究对象中去解决问题.
一、指数幂和对数的运算1.(2018·全国Ⅲ卷)设a=lg0.20.3,b=lg20.3,则( )A.a+b
[解析] 令h(x)=-x-a,则g(x)=f(x)-h(x).在同一坐标系中画出y=f(x),y=h(x)图象的示意图,如图所示.
若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象,可知当直线y=-x-a过点(0,1)时,有2个交点,此时1=-0-a,∴a=-1.
当y=-x-a的图象在y=-x+1的图象上方,即a<-1时,仅有1个交点,不符合题意.当y=-x-a的图象在y=-x+1的图象下方,即a>-1时,有2个交点,符合题意.综上,a的取值范围为[-1,+∞).故选C.
六、函数模型及应用8.(2014·北京卷)加工爆米花时,爆开且不煳的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为( )
A.3.50分钟B.3.75分钟C.4.00分钟D.4.25分钟
所以p=-0.2t2+1.5t-2=-0.2(t-3.75)2+0.812 5,所以当t=3.75时,可食用率p取得最大值.故最佳加工时间为3.75分钟.
人教A版 (2019)必修 第一册4.3 对数教学ppt课件: 这是一份人教A版 (2019)必修 第一册4.3 对数教学ppt课件,共33页。PPT课件主要包含了x=logaN,lgN,lnN,预习自测,对数的性质,答案D等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.3 对数课堂教学课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册4.3 对数课堂教学课件ppt,共20页。PPT课件主要包含了预学案,共学案,logaN,lgN,lnN,答案C,x=logaN,-1=x,答案AD,答案B等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数本章综合与测试优质课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数本章综合与测试优质课件ppt,共55页。PPT课件主要包含了答案1,对数函数的运算,答案C等内容,欢迎下载使用。













