



- 新教材2021-2022学年数学人教A版必修第一册课件:5.5.2+简单的三角恒等变换+【高考】 课件 2 次下载
- 新教材2021-2022学年数学人教A版必修第一册课件:5.6+函数y=Asin(ωx+φ)+【高考】 课件 3 次下载
- 新教材2021-2022学年数学人教A版必修第一册课件:5.7+三角函数的应用+【高考】 课件 3 次下载
- 新教材2021-2022学年数学人教A版必修第一册课件:5.5.1+第2课时+两角和与差的正弦、余弦与正切公式(一)+【高考】 课件 3 次下载
- 新教材2021-2022学年数学人教A版必修第一册课件:5.5.1+第3课时+两角和与差的正弦、余弦与正切公式(二)+【高考】 课件 3 次下载
人教A版 (2019)必修 第一册第五章 三角函数本章综合与测试完整版课件ppt
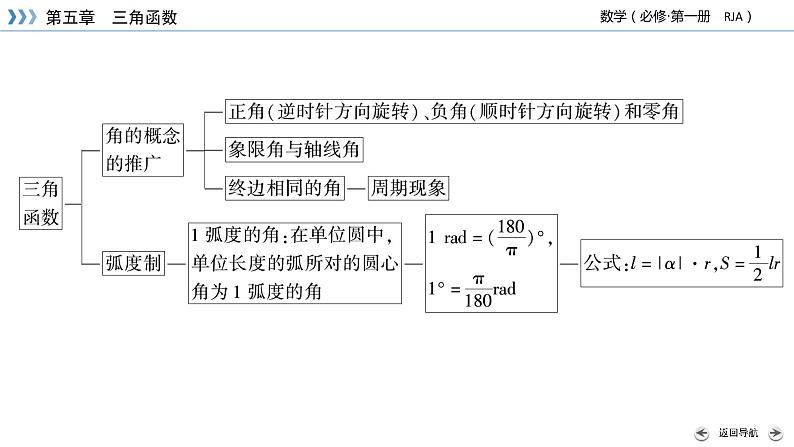
展开1.弧度制建立的意义角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
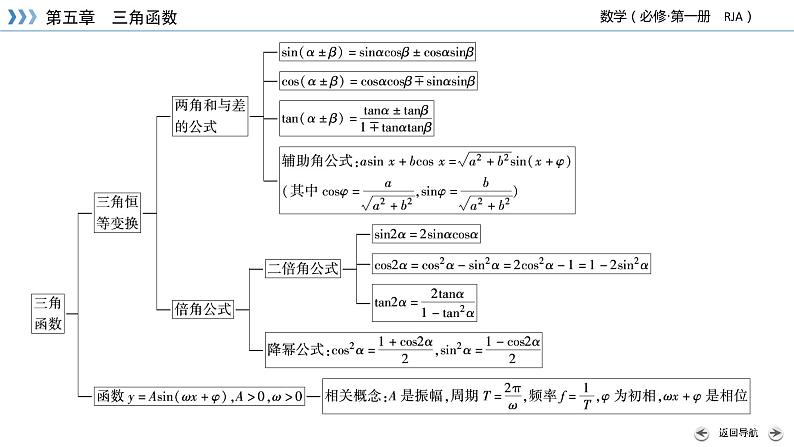
4.和角公式与差角公式S(α+β),C(α+β),T(α+β),S(α-β),C(α-β),T(α-β)这6个和与差的三角函数公式之间具有紧密的联系(有时可以互相转化),这种联系可用框图形式表示,如图所示.
5.由函数y=sinx的图象变换得到y=Asin(ωx+φ)(A>0,ω>0)图象的步骤
6.利用数据建立函数模型问题(1)建立三角函数模型解决实际问题时,首先要寻找与角有关的信息,确定选用正弦、余弦还是正切型函数模型;其次是搜集数据,建立函数解析式并解题;最后将所得结果翻译成实际答案,要注意根据实际作答.(2)拟合已知数据的关键是准确地画出散点图,然后根据散点图中各个角的分布情况确定拟合函数,再利用拟合函数解决相应的问题.
(3)函数拟合获得模型的方法步骤:①根据原始数据、表格绘出散点图;②通过观察散点图,画出“最贴近”的直线或曲线,即拟合直线或拟合曲线;③根据所学函数知识,求出拟合直线或拟合曲线的函数关系式;④利用函数关系式,根据题意对所给问题进行预测和控制,以便为决策和管理提供依据,最终解决问题.
[分析] 根据三角函数的有界性求a,b,利用正弦型函数整体性,求单调区间.
[分析] (1)利用倍角公式、同角三角函数基本关系式及诱导公式化简求值;(2)利用同角三角函数基本关系式、诱导公式及两角和与差的正余弦公式化简求值.
[归纳提升] 三角函数式化简的分类与解题技巧1.三角函数式的化简,主要有以下几类:(1)三角的和式,基本思路是降幂、消项和逆用公式;(2)三角的分式,基本思路是分子与分母的约分和逆用公式,最终变成整式或较简式子;(3)二次根式,则需要运用倍角公式的变形形式.在具体过程中体现的是化归思想,是一个“化异为同”的过程,涉及切弦互化,即“函数名”的“化同”;角的变换,即“单角化倍角”“单角化复角”“复角化复角”等具体手段,以实现三角函数式的化简.
2.化简三角函数式时:(1)若切函数、弦函数共存时,可利用切化弦;(2)若含分式三角函数的问题,一般需分子、分母化简后出现公因式,以便于约分.
[分析] 2α+β=α+(α+β),β=(α+β)-α,可先将条件式3sinβ=sin(2α+β)展开后求α+β的正切值.
[归纳提升] 三角函数式求值的类型与方法三角函数式的求值主要有三种类型:一是给角求值;二是给值求值;三是给值求角.1.给角求值:这类题目的解法相对简单,主要是利用所学的诱导公式、同角三角函数的基本关系式、两角和与差的正弦、余弦、正切公式及二倍角公式等,化非特殊角为特殊角,在转化过程中要注意上述公式的正用及逆用.
2.给值求值:这类题目的解法较上类题目灵活、多变,主要解答方法是利用三角恒等变换中的拆角变换及同角三角函数的基本关系式,和、差、倍、半角公式的综合应用.由于此类题目在解答过程中涉及的数学方法及数学思想相对较多,因此也是平时乃至高考考查的一个热点.
3.已知三角函数值求角问题,通常分两步:(1)先求角的某个三角函数值(由题中已知名称和范围确定),确定求所求角的哪种三角函数值,要根据具体题目,结合所给角的范围确定.(2)根据角的范围确定角.必要时,可利用值缩小角的范围.几种形式的题目本质上都是“给值求值”,只不过往往求出的值是特殊角的值,在求出角之前还需结合函数的单调性确定角,必要时还要讨论角的范围.
[归纳提升] 三角函数恒等式的证明策略三角函数恒等式的证明包括无条件三角函数恒等式的证明和有条件三角函数恒等式的证明.对于无条件三角函数恒等式的证明,要认真分析等式两边三角函数式的特点,找出差异,化异角为同角,化异次为同次,化异名为同名,寻找证明的突破口.对于有条件三角函数等式的证明,要认真观察条件式与被证式的区别与联系,灵活使用条件等式,通过代入法、消元法等方法进行证明.
2.图象变换的途径由函数y=sinx的图象通过变换得到y=Asin(ωx+φ)的图象,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.
[归纳提升] 本题以实际问题为背景,考查了三角函数的应用等基础知识,体现了高考对基础知识的考查.本题属于常规问题,以角为自变量,构造函数并求值,在求解时,要注意函数的定义域.本题有效地考查了数学建模这一核心素养,要求学生能够选择合适的数学模型表达所要解决的数学问题,理解模型中参数的意义,知道如何确定参数,建立模型,求解模型,能够根据问题的实际意义检验结果,完善模型,解决问题.
9.(2018·全国Ⅰ卷)已知函数f(x)=2cs2x-sin2x+2,则( )A.f(x)的最小正周期为π,最大值为3B.f(x)的最小正周期为π,最大值为4C.f(x)的最小正周期为2π,最大值为3D.f(x)的最小正周期为2π,最大值为4
高中数学人教A版 (2019)必修 第一册第五章 三角函数本章综合与测试课文内容ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数本章综合与测试课文内容ppt课件,共39页。PPT课件主要包含了内容索引,知识网络整合构建,题型突破深化提升,答案D等内容,欢迎下载使用。
数学必修 第一册5.7 三角函数的应用优秀ppt课件: 这是一份数学必修 第一册5.7 三角函数的应用优秀ppt课件,共39页。PPT课件主要包含了必备知识•探新知,周期现象,知识点1,三角函数模型的作用,基础知识,知识点2,基础自测,关键能力•攻重难,题型探究,误区警示等内容,欢迎下载使用。
数学必修 第一册5.2 三角函数的概念优质ppt课件: 这是一份数学必修 第一册5.2 三角函数的概念优质ppt课件,共60页。PPT课件主要包含了必备知识•探新知,知识点,基础知识,基础自测,cos80°,关键能力•攻重难,题型探究,误区警示,学科素养,课堂检测•固双基等内容,欢迎下载使用。













