2019-2020学年天津市红桥区七上期末数学试卷

这是一份2019-2020学年天津市红桥区七上期末数学试卷，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共12小题；共60分）
1. −12 的相反数是
A. 12B. −12C. 2D. −2

2. 过度包装既浪费资源又污染环境．据测算，如果全国每年减少 10% 的过度包装纸用量，那么可减排二氧化碳 3120000 吨，把数 3120000 用科学记数法表示为
A. 3.12×105B. 3.12×106C. 31.2×105D. 0.312×107

3. 下列四个数中，最小的数是
A. −∣−3∣B. ∣−32∣C. −−3D. −13

4. 下列方程中，解为 x=−2 的方程是
A. 4x=2B. 3x+6=0C. 13x=3D. 7x−14=0

5. 如图是由几个相同的正方体搭成的一个几何体，从正面看到的平面图形是
A. B.
C. D.

6. 下列结论中正确的是
A. 单项式 πxy24 的系数是 14，次数是 4
B. 单项式 −xy2z 的系数是 −1，次数是 4
C. 单项式 m 的次数是 1，没有系数
D. 多项式 2x2+xy2+3 二次三项式

7. 若 ∠α 与 ∠β 互为补角，∠β 是∠ α 的 2 倍，则 ∠α 为
A. 30∘B. 40∘C. 60∘D. 120∘

8. 甲、乙两地相距 270 千米，从甲地开出一辆快车，速度为 120 千米/时，从乙地开出一辆慢车，速度为 75 千米/时，如果两车相向而行，慢车先开出 1 小时后，快车开出，那么再经过多长时间两车相遇?若设再经过 x 小时两车相遇，则根据题意列方程为
A. 75×1+120−75x=270B. 75×1+120+75x=270
C. 120x−1+75x=270D. 120×1+120+75x=270

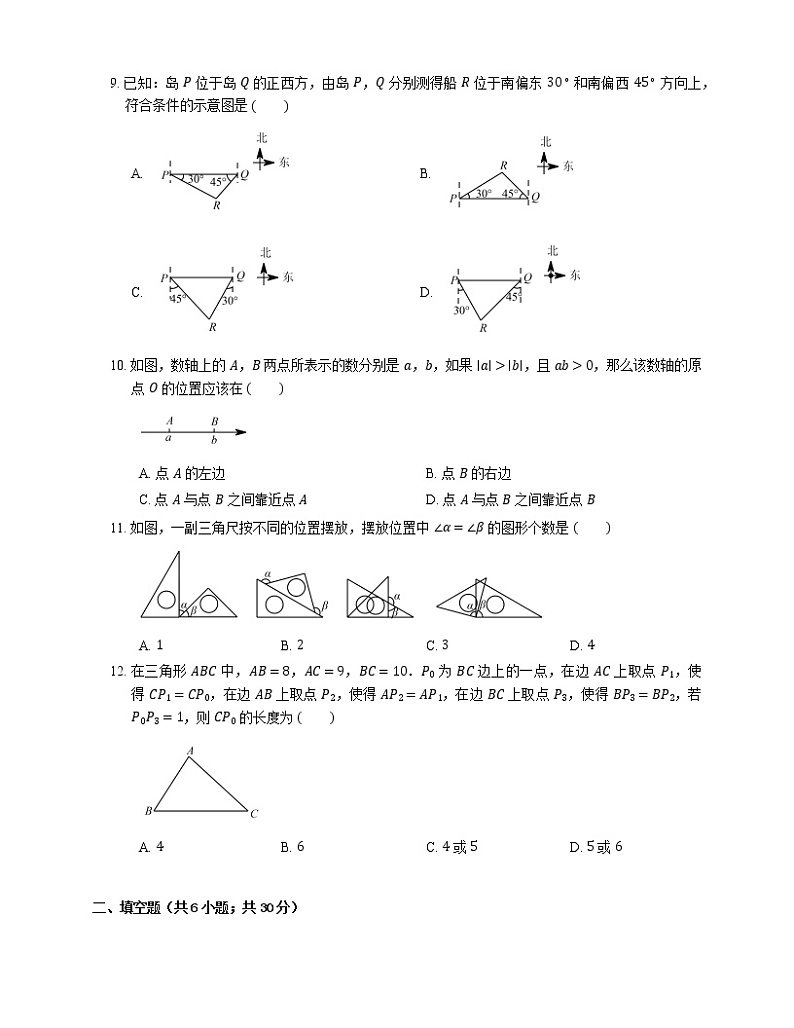
9. 已知：岛 P 位于岛 Q 的正西方，由岛 P，Q 分别测得船 R 位于南偏东 30∘ 和南偏西 45∘ 方向上，符合条件的示意图是
A. B.
C. D.

10. 如图，数轴上的 A，B 两点所表示的数分别是 a，b，如果 ∣a∣>∣b∣，且 ab>0，那么该数轴的原点 O 的位置应该在
A. 点 A 的左边B. 点 B 的右边
C. 点 A 与点 B 之间靠近点 AD. 点 A 与点 B 之间靠近点 B

11. 如图，一副三角尺按不同的位置摆放，摆放位置中 ∠α=∠β 的图形个数是
A. 1B. 2C. 3D. 4

12. 在三角形 ABC 中，AB=8，AC=9，BC=10．P0 为 BC 边上的一点，在边 AC 上取点 P1，使得 CP1=CP0，在边 AB 上取点 P2，使得 AP2=AP1，在边 BC 上取点 P3，使得 BP3=BP2，若 P0P3=1，则 CP0 的长度为
A. 4B. 6C. 4 或 5D. 5 或 6

二、填空题（共6小题；共30分）
13. 黄山主峰一天早晨气温为 −1∘C，中午上升了 8∘C，夜间又下降了 10∘C，那么这天夜间黄山主峰的气温是 ．

14. 用"度分秒"来表示：8.31 度= 度 分 秒．

15. 如图，已知线段 AB=8 cm，延长线段 AB 到 C，使 BC=2AB，点 D 是线段 AC 的中点，则 BD 等于 cm．

16. 若 x=2 是关于 x 的方程 ax+6=2ax 的解，则 a= ．

17. 如图是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面与“生”相对应的面上的汉字是 ．

18. 商店为了对某种商品促销，将定价为 3 元的商品，以下列方式优惠销售：若购买不超过 5 件，按原价付款；若一次性购买 5 件以上，超过部分打八折．如果用 27 元钱，最多可以购买该商品的件数是 ．

三、解答题（共6小题；共78分）
19. 计算题：
（1）−18+6+7−5；
（2）−23×1−14−2−5；
（3）−34×−32×−232−2．

20. 解下列方程：
（1）5x−3=3x+9；
（2）3x−72−1+x3=1；
（3）1+x−12=x+26．

21. 求 3x2+x+3x2−23x−6x2+x 的值，其中 x=−6．

22. 如图，直线 BC 与 MN 相交于点 O，AO⊥BC．
（1）分别写出图中与 ∠AOM 互余和互补的角；
（2）已知 OE 平分 ∠BON，且 ∠EON=20∘，求 ∠AOM 的度数．

23. 一些相同的房间需要粉刷墙面．一天 3 名一级技工去粉刷 8 个房间，结果其中有 50 m2 墙面未来得及粉刷；同样时间内 5 名二级技工粉刷了 10 个房间之外，还多粉刷了另外的 40 m2 墙面，已知每名同级别的技工每天的工作效率相同，每名一级技工比二级技工一天多粉刷 10 m2 墙面．求每个一级技工和二级技工每天粉刷的墙面各是多少平方米?

24. 如图①，将笔记本活页一角折过去，使角的顶点 A 落在 Aʹ 处，BC 为折痕．
（1）图①中，若 ∠1=30∘，求 ∠AʹBD 的度数；
（2）如果又将活页的另一角斜折过去，使 BD 边与 BAʹ 重合，折痕为 BE，如图②所示，∠1=30∘，求 ∠2 以及 ∠CBE 的度数；
（3）如果在图②中改变 ∠1 的大小，则 BAʹ 的位置也随之改变，那么问题（2）中 ∠CBE 的大小是否改变?请说明理由．
答案
第一部分
1. A
2. B
3. A
4. B
5. D
6. B
7. C
8. B【解析】设再经过 x 小时两车相遇，则根据题意列方程为
75×1+120+75x=270 .
9. D
10. B
11. C
12. D
第二部分
13. −3∘C
14. 8，18，36
15. 4
16. 3
17. 学
18. 10 件．
【解析】五件原价需 5×3=15（元）．
余下的每件八折还可买 27−15÷0.8×3=5（件）．
5+5=10（件）．
第三部分
19. （1） 原式=−23+13=−10.
（2） 原式=−8×34−2+5=−8+5=−3.
（3） 原式=−34×−6=92.
20. （1）
5x−3x=9+3,2x=12,
解得：
x=6;
（2）
33x−7−21+x=6,9x−21−2−2x=6,7x=29,
解得：
x=297;
（3）
6+3x−1=x+2,6+3x−3=x+2,2x=−1,
解得：
x=−0.5.
21. 原式=3x2+x+3x2−2x−6x2−x=−2x.
当 x=−6 时，
原式=−2×−6=12.
22. （1） 与 ∠AOM 互余的角是：∠COM，∠BON．
互补的角是：∠AON．
（2） ∵OE 平分 ∠BON，
∴∠BON=2∠EON=40∘．
∴∠COM=∠BON=40∘．
∵AO⊥BC，
∴∠AOC=90∘．
∴∠AOM=90∘−∠COM=90∘−40∘=50∘．
23. 设每个二级技工每天刷 x m2，则每个一级技工每天刷 x+10m2，
依题意得
5x−4010=3x+10+508,
解得
x=112,x+10=122,
答：每个一级和二级技工每天粉刷的墙面各是 122 平方米 和 112 平方米．
24. （1） ∵∠1=30∘，
∴∠1=∠ABC=30∘，
∴∠AʹBD=180∘−30∘−30∘=120∘．
（2） ∵∠AʹBD=120∘，∠2=∠DBE，
∴∠2=12∠AʹBD=60∘，
∴∠CBE=∠1+∠2=30∘+60∘=90∘．
（3） 结论：∠CBE 的大小不变．理由如下，
∵∠1=12∠ABAʹ，∠2=12∠AʹBD，∠ABAʹ+∠AʹBD=180∘，
∴∠1+∠2=12∠ABAʹ+12∠AʹBD=12∠ABAʹ+∠AʹBD=12×180∘=90∘.
即 ∠CBE=90∘．