2019-2020学年成都市金堂县八下期末数学试卷

这是一份2019-2020学年成都市金堂县八下期末数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 观察出下列四种汽车标志，其中既是中心对称图形，又是轴对称图形的是
A. B.
C. D.

2. 若 x>y，则下列式子中错误的是
A. x−3>y−3B. x3>y3C. x+3>y+3D. −3x>−3y

3. 若分式 xx+3 有意义，则 x 应满足的条件是
A. x≠0B. x≠−3C. x≥−3D. x≤−3

4. 下列四个多项式中，能因式分解的是
A. a2+1B. x2+5yC. x2−5yD. a2−6a+9

5. 若一个正多边形的一个外角是 45∘，则这个正多边形的边数是
A. 10B. 9C. 8D. 6

6. 不等式组 x+2>0,2x−6≤0 的解集在数轴上表示正确的是
A. B.
C. D.

7. 分式方程 2x+1x−2=1 的解为
A. x=−12B. x=−1C. x=−2D. x=−3

8. 如图，在 △ABC 中，AC=10，BC=8，AB 垂直平分线交 AB 于点 M，交 AC 于点 D，则 △BDC 的周长为
A. 14B. 16C. 18D. 20

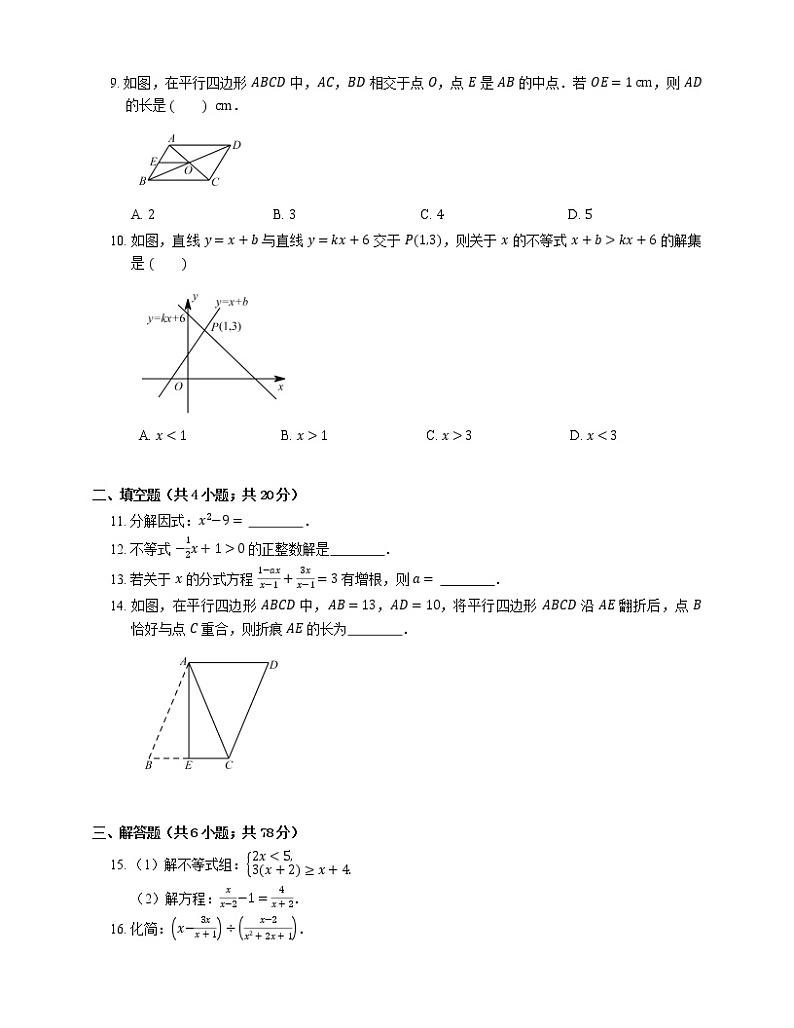
9. 如图，在平行四边形 ABCD 中，AC，BD 相交于点 O，点 E 是 AB 的中点．若 OE=1 cm，则 AD 的长是 cm．
A. 2B. 3C. 4D. 5

10. 如图，直线 y=x+b 与直线 y=kx+6 交于 P1,3，则关于 x 的不等式 x+b>kx+6 的解集是
A. x<1B. x>1C. x>3D. x<3

二、填空题（共4小题；共20分）
11. 分解因式：x2−9= ．

12. 不等式 −12x+1>0 的正整数解是 ．

13. 若关于 x 的分式方程 1−axx−1+3xx−1=3 有增根，则 a= ．

14. 如图，在平行四边形 ABCD 中，AB=13，AD=10，将平行四边形 ABCD 沿 AE 翻折后，点 B 恰好与点 C 重合，则折痕 AE 的长为 ．

三、解答题（共6小题；共78分）
15. （1）解不等式组：2x<5,3x+2≥x+4.
（2）解方程：xx−2−1=4x+2．

16. 化简：x−3xx+1÷x−2x2+2x+1．

17. 如图，在平行四边形 ABCD 中，∠ABC 的平分线交 AD 于点 E，过点 D 作 BE 的平行线交于 BC 于点 F．
（1）求证：△ABE≌△CDF；
（2）若 AB=6，BC=8，求 DE 的长．

18. 如图，在边长为 1 的小正方形网格中，△AOB 的顶点均在格点上．
（1）B 点关于 y 轴的对称点坐标为 ；
（2）将 △AOB 向左平移 3 个单位长度得到 △A1O1B1，请画出 △A1O1B1；
（3）以原点 O 为对称中心，画出 △AOB 关于原点对称的 △A2OB2；
（4）以原点 O 为旋转中心，画出把 △AOB 顺时针旋转 90∘ 的图形 △A3OB3．

19. 某工厂甲、乙两人加工同一种零件，每小时甲比乙多加工 10 个这种零件，甲加工 150 个这种零件所用的时间与乙加工 120 个这种零件所用的时间相等．
（1）甲、乙两人每小时各加工多少个这种零件?
（2）该工厂计划加工 920 个零件，甲参与加工这批零件不超过 12 天，则乙至少加工多少天才能加工完这批零件?

20. 如图，△ABC 和 △DBE 均为等腰三角形，点 A，D，E 在同一直线上，连接 CE．
（1）如图 1，若 ∠BAC=∠BCA=∠BDE=∠BED=55∘．
①求证：AD=CE；
②求 ∠AEC 的度数．
（2）如图 2，若 ∠ABC=∠DBE=120∘，BM 为 △BDE 中 DE 边上的高，CN 为 △ACE 中 AE 边上的高，CN=a，BM=b，试证明：AE=233a+23b．

四、填空题（共5小题；共25分）
21. 若 x+y−1=0，则 12x2+xy+12y2−2= ．

22. 有 5 张正面分别标有数字 −2，0，2，4，6 的不透明卡片，它们除数不同外其余全部相同，先将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为 a，则使关于 x 的不等式组 x>3x−4,3x−a>5 有实数解的概率为 ．

23. 若关于 x 的方程 x+kx+1−1=kx−1 的解为负数，则 k 的取值范围是 ．

24. 如图，等边三角形 △ABC 的边长为 4，过点 C 的直线 m⊥AC，且 △ABC 与 △AʹBʹC 关于直线 m 对称，D 为线段 BʹC 上一动点，则 AD+BD 的最小值是 ．

25. 一组正方形按如图所示的方式放置，其中顶点 B1 在 y 轴上，顶点 C1，E1，E2，C2，E3，E4，C3⋯ 在 x 轴上，已知正方形 A1B1C1D1 的边长为 1，∠B1C1O=60∘，B1C1∥B2C2∥B3C3⋯ 则正方形 A2017B2017C2017D2017 的边长是 ．

五、解答题（共3小题；共39分）
26. 金堂骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场，某车行经营的A型车去年 2 月份销售总额为 3.2 万元，今年经过改造升级后A型车每辆销售价比去年增加 400 元，若今年 2 月份与去年 2 月份卖出的A型车数量相同，则今年 2 月份A型车销售总额将比去年 2 月份销售总额增加 25%．
（1）求今年 2 月份A型车每辆销售价多少元?
（2）该车行计划今年 3 月份新进一批A型车和B型车共 50 辆，且B型车的进货数量不超过A型车数量的 2 倍，A，B两种型号车的进货和销售价格如表，问应如何进货才能使这批车获利最多?
A型车B型车进货价格元/辆11001400销售价格元/辆今年的销售价格2400

27. 如图 1，四边形 ABCD 是正方形，在 AB 的延长线上取一点 E，连接 EC，过点 C 作 CF⊥EC 交 AD 于点 F．
（1）求证：EC=FC．
（2）若 G，M 分别是 AB，CD 上一动点，连接 GM．H 是 GM 上的中点，连接 BH，当 G，M 运动到某一特殊位置时得到 BH=BG+CM，此时 ∠ABH 的度数是多少?请说明理由．
（3）如图 2，在（2）的条件下，若 BG=1，MC=3，连接 AH．求出四边形 △AHMD 的面积．

28. 如图，边长为 a 正方形 OABC 的边 OA，OC 在坐标轴上．在 x 轴上线段 PQ=a（Q 在 A 的右边），P 从 A 出发，以每秒 1 个单位的速度向 O 运动，当点 P 到达点 O 时停止运动，运动时间为 ts．连接 PB，过点 P 作 PB 的垂线，过点 Q 作 x 轴的垂线，两垂线相交于点 D．连接 BD 交 y 轴于点 E，设 PD 交 y 轴于点 F，连接 PE．
（1）求 ∠PBD 的度数．
（2）设 △POE 的周长为 l，探索 l 与 t 的函数关系式，并写出 t 的取值范围．
（3）令 a=4，当 △PBE 为等腰三角形时，求 △EFD 的面积．
答案
第一部分
1. B【解析】A、不是轴对称图形，
B、既是中心对称图形，又是轴对称图形，
C、是轴对称图形，
D、是中心对称图形．
2. D
3. B【解析】由题意可知：x+3≠0，
∴x≠−3．
4. D【解析】a2−6a+9=a−32．
5. C
【解析】∵ 多边形外角和 =360∘，
∴ 这个正多边形的边数是 360∘÷45∘=8．
6. C【解析】x+2>0, ⋯⋯①2x−6≤0, ⋯⋯②
由 ① 得 x>−2．
由 ② 得 x≤3
故不等式组的解集为：−2在数轴上表示为：
7. D【解析】等号两边同时乘以 x−2，得 2x+1=x−2，
解得 x=−3，
经检验 x=−3 是原方程的解，
则是原方程的解是 x=−3．
8. C【解析】∵ 边 AB 的垂直平分线交 AC 于点 D，AC=10，BC=8，
∴AD=BD，
∴△BDC 的周长为 BC+CD+BD=BC+CD+AD=BC+AC=8+10=18．
9. A【解析】∵ 四边形 ABCD 为平行四边形，
∴BO=DO，
∵ 点 E 是 AB 的中点，
∴OE 为 △ABD 的中位线，
∴AD=2OE，
∵OE=1 cm，
∴AD=2 cm．
10. B
【解析】当 x>1 时，x+b>kx+6，即不等式 x+b>kx+6 的解集为 x>1．
第二部分
11. x+3x−3
12. x=1
【解析】∵−12x+1>0，
∴−12x>−1，
∴x<2，则不等式的正整数解是 x=1．
13. 4
【解析】方程两边同时乘 x−1，可得 1−ax+3x=3x−1，
整理可得 ax=4，
∵ 分式方程有增根，
∴ 方程的根为 x=1，
∴a=4．
14. 12
【解析】由翻转变换的性质可知，∠AEB=90∘，BE=12BC=5，
由勾股定理得，AE=AB2−BE2=12．
第三部分
15. （1）
2x<5, ⋯⋯①3x+2≥x+4. ⋯⋯②
由 ① 得：
x<52.
由 ② 得：
x≥−1.∴
原不等式组的解集为 −1≤x<52．
（2）
x2+2x−x2+4=4x−8,
解得：
x=6,
经检验：x=6 是分式方程的根．
故原分式方程的解为 x=6．
16. x−3xx+1÷x−2x2+2x+1=x2+x−3xx+1⋅x+12x−2=xx−2x+1⋅x+12x−2=xx+1=x2+x.
17. （1） ∵ 四边形 ABCD 是平行四边形
∴AD∥BC，AD=BC，AB=CD，∠A=∠C，
∵BE∥DF，
∴ 四边形 BEDF 是平行四边形，
∴DE=BF，
∴AD−DE=BC−BF，即：AE=CF，
在 △ABE 和 △CDF 中，
AB=CD,∠A=∠C,AE=CF,
∴△ABE≌△CDF．
（2） ∵AD∥BC，
∴∠EBF=∠AEB，
又 ∵BE 平分 ∠ABC，
∴∠EBF=∠ABE，
∴∠AEB=∠ABE，
∴AE=AB=6，
又 ∵BC=AD=8，
∴DE=AD−AE=2．
18. （1） −3,2
【解析】由图可得，B 点关于 y 轴的对称点坐标为 −3,2．
（2） 如图 1，△A1O1B1 为所求作的图形．
（3） 如图 2：△A2OB2 为所求作的图形．
（4） 如图 3：△A3OB3 为所求作的图形．
19. （1） 设乙每小时加工零件 x 个，则甲每小时加工零件 x+10 个，
由题可得：
120x=150x+10.
解得：
x=40.
经检验：x=40 是原方程的解，且符合题意，
则 x+10=50，
答：甲每小时加工零件 50 个，乙每小时加工零件 40 个．
（2） 设乙加工 y 天才能加工完这批零件，则
920−40y50≤12.
解得：
y≥8.
答：乙至少加工 8 天才能加工完这批零件．
20. （1） ① ∵∠ABD+∠DBC=∠CBE+∠DBC=70∘，
∴∠ABD=∠CBE．
∵△ABC 和 △DBE 均为以点 B 为腰上顶点的等腰三角形．
∴BA=BC，BD=BE，
在 △ABD 和 △CBE 中，
AB=CB,∠ABD=∠CBE,BD=BE,
∴△ABD≌△CBE．
∴AD=CE．
② ∵△ABD≌△CBE，
∴∠BDA=∠BEC=180∘−∠BDE，
∵∠AEC=∠BEC−∠BED，
∴∠AEC=180∘−2∠BDE=70∘．
（2） 同理可证：AD=CE，∠AEC=120∘，
∴∠CEN=60∘，
∵CN 为 △ACE 中 AE 边上的高，
∴∠ECN=30∘，
∵ 在 Rt△CEN 中，CN=a，∠ECN=30∘，
∴ 根据勾股定理得，CE=233a，
∴AD=CE=233a，
∵△DBE 为等腰三角形，BM 为 △BDE 中 DE 边上的高，
∴DE=2DM，
∵∠DBE=120∘，
∴∠BDM=30∘，
在 Rt△BDM 中，根据勾股定理得，DM=3b，
∴DE=2DM=23b，
∴AE=AD+DE=233a+23b．
第四部分
21. −32
【解析】∵x+y−1=0，
∴x+y=1，
∴ 12x2+xy+12y2−2=12x+y2−2=12×12−2=−32.
22. 25
【解析】x>3x−4, ⋯⋯①3x−a>5, ⋯⋯②
解 ① 得 x<2，
解 ② 得 x>5+a3，
不等式组有实数解，则 2>5+a3，解得 a<1，
∴ 任取一张，将该卡片上的数字记为 a，则使关于 x 的不等式组 x>3x−4,3x−a>5 有实数解的概率为 25．
23. k>12 且 k≠1
【解析】去分母得：x+kx−1−x+1x−1=kx+1，
整理得：x2+kx−x−k−x2+1=kx+k，
解得：x=−2k+1，
由分式方程的解为负数，得到 −2k+1<0 且 −2k+1≠−1，
解得：k>12 且 k≠1．
24. 8
【解析】连接 BBʹ，如图所示．
∵△ABC，△AʹBʹC 均为正三角形，
∴∠ACB=∠Aʹ=60∘，AʹC=BC=AʹBʹ，
∴AʹBʹ∥BC，
∴ 四边形 AʹCBBʹ 为菱形，
∴ 点 B 关于 BʹC 对称的点是 Aʹ，
∴ 当点 D 与点 C 重合时，AD+BD 取最小值，此时 AD+BD=4+4=8．
25. 332016
【解析】∵∠B1C1O=60∘，B1C1∥B2C2∥B3C3，
∴∠D1C1E1=∠C2B2E2=∠C3B3E4=30∘，
∴D1E1=C1D1sin30∘=12，
则 B2C2=B2E2cs30∘=1232=331，
同理可得：B3C3=13=332，
故正方形 AnBnCnDn 的边长是：33n−1．
则正方形 A2017B2017C2017D2017 的边长是：332016．
第五部分
26. （1） 设去年 2 月份A型车每辆的售价为 x 元，则今年 2 月份A型车每辆的售价为 x+400 元，
根据题意得：
32000x=32000×1+25%x+400.
解得：
x=1600.
经检验，x=1600 是原方程的解，且符合题意，
则 x+400=2000．
答：今年 2 月份A型车每辆销售价为 2000 元．
（2） 设购进A型车 m 辆，获得的总利润为 w 元，则购进B型车 50−m 辆，
根据题意得：w=2000−1100m+2400−140050−m=−100m+50000．
又 ∵50−m≤2m，
∴m≥1623．
∵k=−100<0，
∴ 当 m=17 时，w 取最大值．
答：购进A型车 17 辆，B型车 33 辆，获利最多．
27. （1） 如题干图 1，
∵ 四边形 ABCD 是正方形，
∴CD=BC，∠D=∠DCB=∠ABC=90∘，
∴∠CBE=180∘−90∘=90∘，
∴∠CBE=∠D，
∵CF⊥EC，
∴∠ECF=90∘，
∴∠ECF−∠BCF=∠BCD−∠BCF，
∴∠DCF=∠BCE，
在 △DCF 和 △BCE 中，
∠D=∠CBE,CD=CB,∠DCF=∠BCE,
∴△DCF≌△BCE，
∴EC=FC．
（2） ∠ABH=60∘，
理由：如图 1，延长 BH 交 CD 于点 N，
∵H 是 MG 的中点，
∴HM=HG，
在正方形 ABCD 中，DC∥AB，
∴∠MNH=∠GBH，∠NMH=∠BGH，
在 △HNM 和 △HBG 中，
∠MNH=∠GBH,∠NMH=∠BGH,MH=GH,
∴△HNM≌△HBG，
∴HN=HB，MN=GB，
∵BH=GB+MC，
∴NC=BH=12BN，
∴∠NBC=30∘，
∴∠ABH=90∘−30∘=60∘．
（3） 如图 3：延长 BH 交 CD 于点 N，作 HP⊥AB 于点 P．
∴∠HPB=90∘，
∴∠PHB=90∘−60∘=30∘，
由（2）得：BH=CN=GB+MC=1+3，
∴BN=23+1，
由勾股定理得：PH=32×3+1=3+32，BC=3×3+1=3+3，
∴S四边形AHMD=S四边形ABND−S△AGH=2+3+3×3+32−3+2×12×3+32=27+1134.
28. （1） ∵∠APB+∠PBA=∠APB+∠DPQ=90∘，
∴∠PBA=∠DPQ，
在 △BAP 和 △PQD 中，
∠PBA=∠DPQ,BA=PQ,∠BAP=∠PQD,
∴△BAP≌△PQD，
∴BP=PD，
又 ∵BP⊥PD，
∴∠PBD=45∘．
（2） 如图 1，延长 PA 至点 M，使得 AM=CE，连接 MB．
在 △BAM 和 △BCE 中，
BA=BC,∠BAM=∠BCE,AM=CE,
∴△BAM≌△BCE，
∴∠MBA=∠EBC，
∵∠EBC+∠ABP=45∘，
∴∠MBP=∠MBA+∠ABP=45∘=∠EBP，
在 △BPM 和 △BPE 中，
BM=BE,∠MBP=∠EBP,BP=BP,
∴△BPM≌△BPE，
∴EP=MP=MA+AP=CE+AP，
又 ∵l=EP+PO+EO=CE+EO+AP+PO=2AO，
∴l=2a0≤t≤a．
（3） ①当 EP=EB 时，如图 2，
∵∠PBD=45∘，
∴EP⊥EB，E 为 BD 中点，即 E 与 C 重合，P 与 O 重合，
此时，S△EFD=8；
②当 PB=PE 时，
∵∠PBD=45∘，
∴EP⊥PB，
此时 E，F，D 三点均与点 O 重合，故 △EFD 不存在；
③当 BP=BE 时，
在 Rt△BAP 和 Rt△BCE 中，
BP=BE,BA=BC,
∴△BAP≌△BCE，
∴CE=AP=t，
∴PE=2t，
又 ∵OE=OP=4−t，
∴PE=24−t，
∴24−t=2t，解得：t=42−4，
∵△BAP≌△PQD，
∴AP=QD，
∴D42−4,42−4，
∵P42−8,0，
∴ 设直线 PD 的解析式为 y=kx+b，
将点 D 、点 P 的坐标代入得 42−4k+b=42−4,42−8k+b=0,
解得 k=2−1,b=122−16,
∴ 直线 PD 的解析式为 y=2−1x+122−16，
∴F0,122−16，
∴EF=24−162，
此时，S△EFD=1652−7．
综上所述：S△EFD=8 或 S△EFD=1652−7．