数学八年级上册14.3 因式分解综合与测试复习ppt课件

这是一份数学八年级上册14.3 因式分解综合与测试复习ppt课件，共23页。PPT课件主要包含了分解因式，运用公式法，十字相乘法，提公因式法，2运用公式法，⑶十字相乘法，典型例题，例1分解因式，因式分解，配套练习等内容，欢迎下载使用。
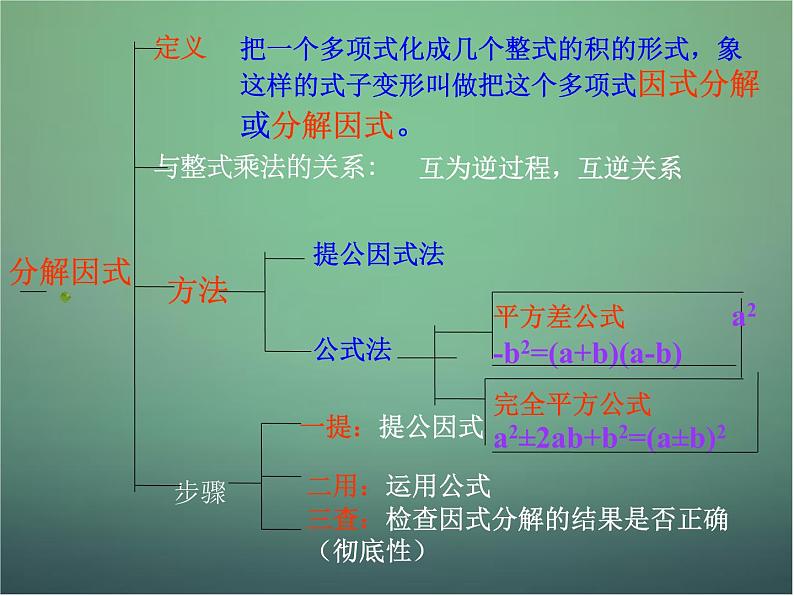
把一个多项式化成几个整式的积的形式，象这样的式子变形叫做把这个多项式因式分解或分解因式。
三查：检查因式分解的结果是否正确 （彻底性）
（二）分解因式的方法：
如果多项式的各项有公因式，可以把这个公因式提到括号外面，将多项式写成乘积的形式。这种分解因式的方法叫做提公因式法。
例题：把下列各式分解因式 ① 6x3y2-9x2y3+3x2y2 ②p（y-x）-q（x-y）③ (x-y)2-y(y-x)2
即： ma + mb + mc = m（a+b+c）
解：原式=3x2y2(2x-3y+1)
解：原式=p(y-x)+q(y-x) =(y-x)(p+q)
解：原式=(x-y) 2(1-y)
① a2－b2＝（a＋b）（a－b） [ 平方差公式 ]
② a2 ＋2ab＋ b2 ＝（a＋b）2 [ 完全平方公式 ] a2 －2ab+ b2 ＝（a－b）2 [ 完全平方公式 ]
运用公式法中主要使用的公式有如下几个：
例题：把下列各式分解因式 ①x2－4y2 ② 9x2-6x+1
解：原式= x2-(2y)2 =（x+2y)(x-2y）
解：原式=(3x)2-2·(3x) ·1+1 =（3x-1)2
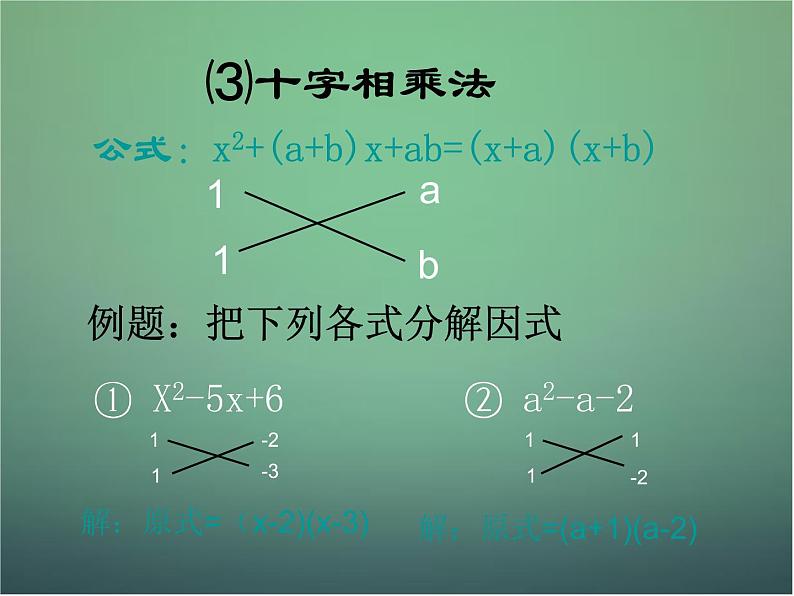
公式：x2+(a+b)x+ab=(x+a)(x+b)
例题：把下列各式分解因式
① X2-5x+6 ② a2-a-2
解：原式=（x-2)(x-3)
解：原式=(a+1)(a-2)
① 对任意多项式分解因式，都必须首先考虑提取公因式。
② 对于二项式，考虑应用平方差公式分解。对于三项式，考虑应用完全平方公式或十字相乘法分解。
③检查：特别看看多项式因式是否分解彻底
1、 若 100x2-kxy+49y2 是一个完全平方式, 则k=（ ）
2、计算(-2)101+(-2)100
3、已知：2x-3=0，求代数式x(x2-x)+x2(5-x)-9的值
解：原式=（-2)(-2)100+ (-2)100
=(-2)100(-2+1)=2100· (-1)=-2100
解：原式=x3-x2+5x2-x3-9 =4x2-9 =(2x+3)(2x-3)
又∵ 2x-3=0, ∴ 原式=0
例3.已知 是一个完全平方式，则a的值是( )A B C D
例4.已知 是一个完全平方式，求k的值。
例7.求证：当n是整数时，两个连续奇数 的平方差是8的倍数。
例8.已知 ，求 的值。
△ABC的三边满足 ，则△ABC是( )A 等腰三角形 B 直角三角形 C 等边三角形 D 锐角三角形
例7.如图，在一块边长为acm的正方形纸板四角，各剪去一个边长为bcm的正方形，计算当时，剩余部分的面积。
8. 如图，某小区规划在边长为x m的正方形场地上，修建两条宽为2m的甬道，其余部分种草，你能用几种方法计算甬道所占的面积？
⑶ -x3y3-2x2y2-xy
(1) 4x2-16y2 (2) x2+xy+ y2.
(4)81a4-b4   
（6) (x-y)2 - 6x +6y+9
⑸(2x+y)2-2(2x+y)+1
⑺ x2y2+xy-12
(8) (x+1)(x+5）+4
解:原式=4(x2-4y2) =4(x+2y)(x-2y)
解:原式=-xy(x2y2+2xy+1) =-xy(xy+1)2
解:原式=(9a2+b2)(9a2-b2) =(9a2+b2)(3a+b)(3a-b)
解：原式=(2x+y-1)2
解：原式=(x-y)2-6(x-y)+9 =(x-y-3)2
解：原式=(xy-4)(xy+3)
解：原式=x2+6x+5+4 =(x+3)2