2020-2021学年第十二章 全等三角形12.2 三角形全等的判定教课内容课件ppt

这是一份2020-2021学年第十二章 全等三角形12.2 三角形全等的判定教课内容课件ppt，共33页。PPT课件主要包含了答至少要有三个条件，探究5，用数学符号表示，探究反映的规律是，AOBO，例题讲解，帮帮我，探究6，中点的定义，对顶角相等等内容，欢迎下载使用。

回首往事：1.什么样的图形是全等三角形？2.判断三角形全等至少要有几个条件？
边边边公理： 有三边对应相等的两个三角形全等。
边角边公理： 有两边和它们夹角对应相等的两个三角形全等。
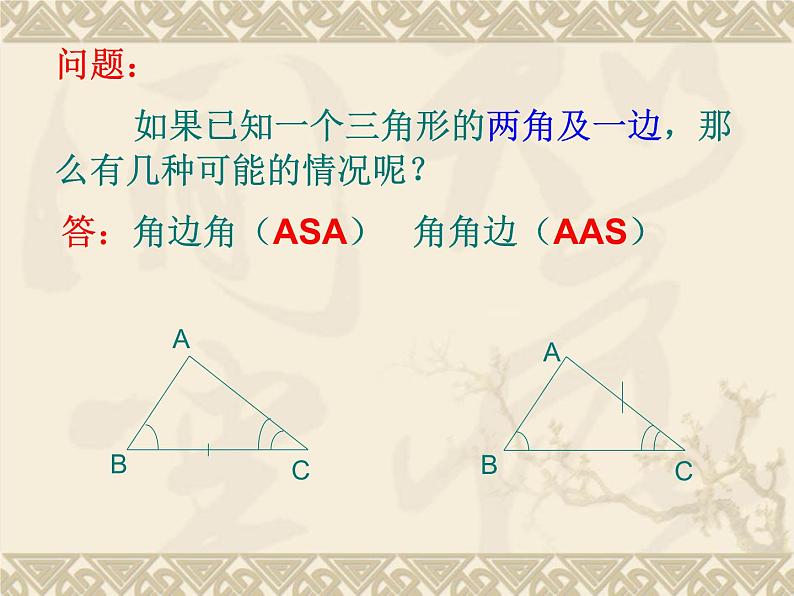
问题： 如果已知一个三角形的两角及一边，那么有几种可能的情况呢？
答：角边角（ASA） 角角边（AAS）
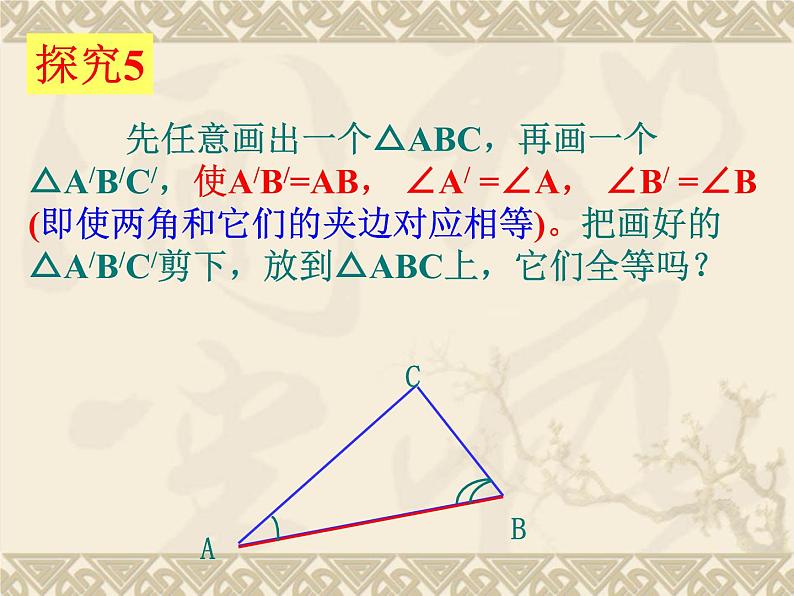
先任意画出一个△ABC，再画一个△A/B/C/，使A/B/=AB， ∠A/ =∠A， ∠B/ =∠B (即使两角和它们的夹边对应相等)。把画好的△A/B/C/剪下，放到△ABC上，它们全等吗？
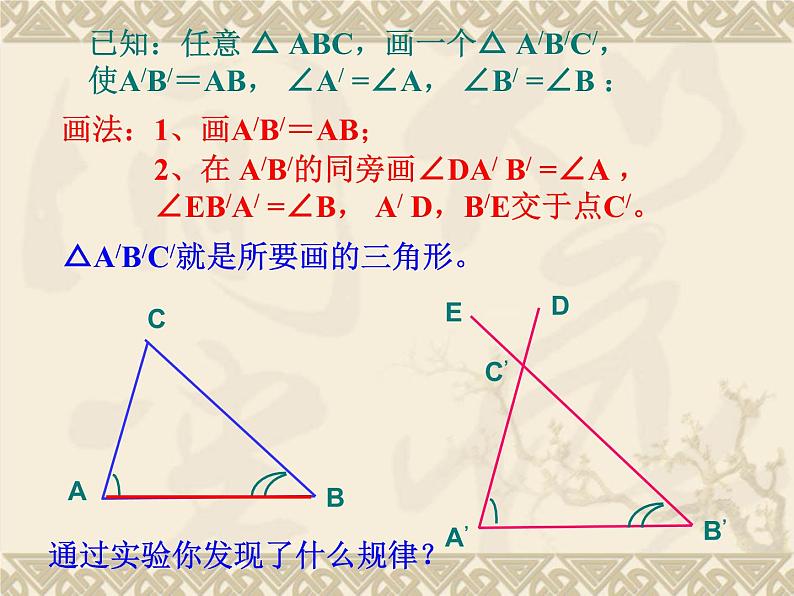
画法：1、画A/B/＝AB；
2、在 A/B/的同旁画∠DA/ B/ =∠A ， ∠EB/A/ =∠B， A/ D，B/E交于点C/。
通过实验你发现了什么规律？
已知：任意 △ ABC，画一个△ A/B/C/，使A/B/＝AB， ∠A/ =∠A， ∠B/ =∠B ：
△A/B/C/就是所要画的三角形。
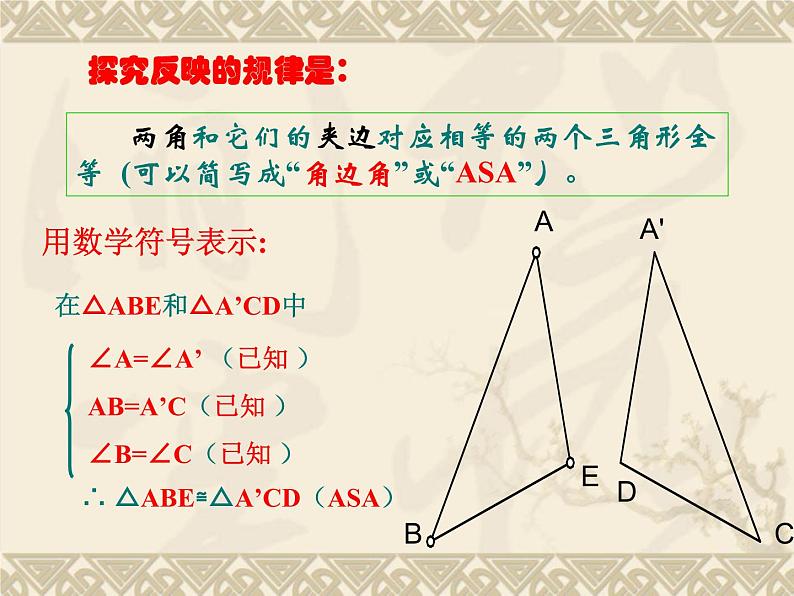
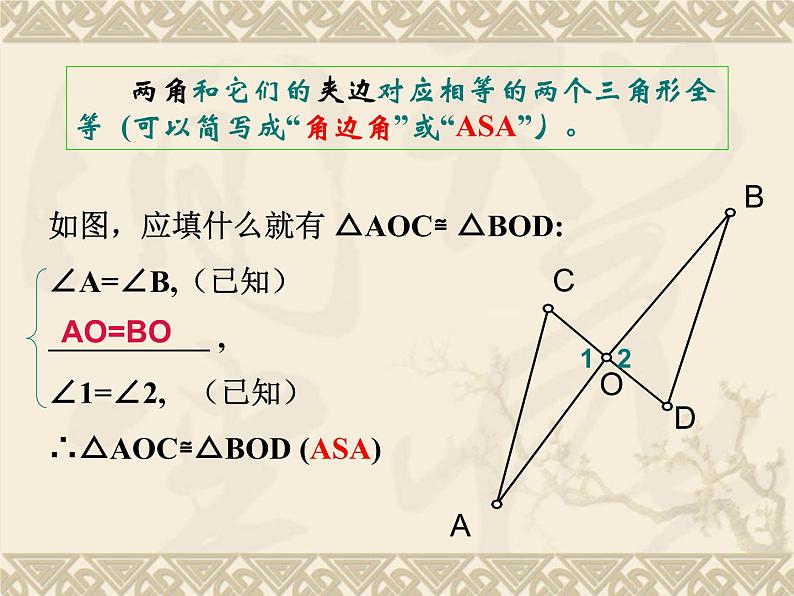
两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角”或“ASA”）。
如图，应填什么就有 △AOC≌ △BOD:∠A=∠B,（已知） ,∠1=∠2, （已知）∴△AOC≌△BOD (ASA)
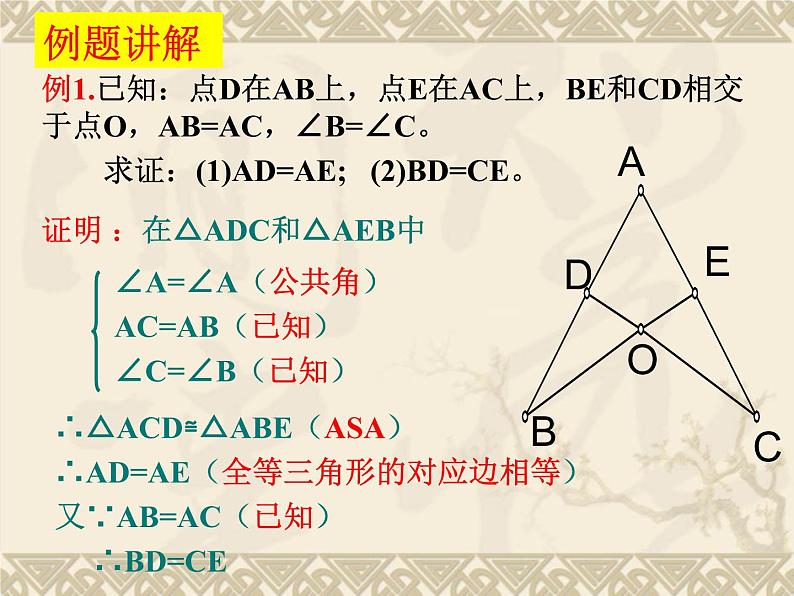
例1.已知：点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C。 求证：(1)AD=AE; (2)BD=CE。
证明 ：在△ADC和△AEB中
∠A=∠A（公共角）AC=AB（已知）∠C=∠B（已知）
∴△ACD≌△ABE（ASA）∴AD=AE（全等三角形的对应边相等）又∵AB=AC（已知） ∴BD=CE
1.如图,O是AB的中点，∠A= ∠B， △AOC与△BOD全等吗?为什么？
2. 如图，点B、E、C、F在一条直线上，AB＝DE，AB∥DE，∠A＝∠D． 求证：BE=CF．
小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢? 如果可以,带哪块去合适呢?为什么?
利用“角边角”可知,带第(2)块去，可以配到一个与原来全等的三角形玻璃。
如下图，在△ABC和△DEF中,∠A ＝∠D, ∠ B＝∠E, BC＝EF, △ABC与△DEF全等吗？能利用角边角条件证明你的结论吗？
在△ABC和△DEF中,∠A +∠B +∠C＝1800, ∠D +∠E +∠F =1800,∵ ∠A ＝∠D, ∠B＝∠E, ∴ ∠C＝∠F, ∴ ∠B＝∠E, BC＝EF, ∠C＝∠F, ∴ △ABC ≌△DEF （ASA）
两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）。
例: 如图,O是AB的中点，∠C= ∠D， △AOC与△BOD全等吗?为什么？
解：在 中
到目前为止,我们一共探索出判定三角形全等的四种规律，它们分别是:
1、边边边 (SSS)
3、角边角 (ASA)
4、角角边 (AAS)
2、边角边 (SAS)
1、如图∠ACB=∠DFE，BC=EF，根据SAS,ASA或AAS， 那么应补充一个直接条件 --------------------------，（写出一个即可），才能使△ABC≌△DEF.
2、如图，BE=CD，∠1=∠2，则AB=AC吗？为什么？
AC=DF或∠B=∠E或∠A=∠D
1. 如图，要测量河两岸相对的两点A，B的距离，可以在AB的垂线BF上取两点C，D，使BC=CD，再定出BF的垂线DE，使A， C，E在一条直线上，这时测得DE的长就是AB的长。为什么？
在△ABC和△EDC中, ∠B=∠EDC=900 BC＝DC, ∠1＝∠2, ∴ △ABC ≌△DEF （ASA）∴ AB＝ED.
2.如图,AB⊥BC, AD⊥DC, ∠1=∠2. 求证: AB=AD.
在△ABC和△ADC中, ∠B=∠D, ∠1＝∠2, AC＝AC, ∴ △ABC ≌△ADC （AAS）∴ AB＝AD.
证明： ∵ AB⊥BC, AD⊥DC,
∴ ∠B=∠D=900,
已知:如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF(1)若要以“SAS”为依据，还缺条件 ＿＿＿＿＿＿； (2)若要以“ASA”为依据，还缺条件 ； (3)若要以“SSS” 为依据，还缺条件 ;
AB=DE、AC=DF
(4)若要以“AAS” 为依据，还缺条件＿＿＿＿＿＿；
4、角角边 (AAS)
(1) 图中的两个三角形全等吗? 请说明理由.
全等 因为两角和其中一角的对边对应相等的两个三角形全等.
(3) 如图，AC、BD交于点O,AC=BD,AB=CD.求证：
证明: (1)连接AD, 在△ADC和△DAB中
AD=DA（公共边）AC=DB（已知）DC=AB（已知）
∴△ADC≌△DAB （SSS）∴∠C=∠B（全等三角形的对应角相等）
(2) 在△ AOB 和△ DOC中
∠ B =∠ C （已证）∠1=∠2 （对顶角相等）DC=AB（已知）
∴△DOC≌△AOB （AAS）∴OA=OD（全等三角形的对应边相等）
-----全等三角形判定
2.如图，ＡＢ∥ＤＣ，ＡＤ∥ＢＣ，说出△ABＤ≌ △ＣＤＢ的理由。
3. 如图，AB=DE，AF=CD，EF=BC，∠A＝∠D，试说明：BF∥CE
4. 如图，在△AFD和△BEC中，点A、E、F、C在同一直线上，有下列四个论断： ①AD=CB，②AE=CF，③∠B＝∠D，④ ∠A＝∠C.请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程。
5. 如图，在△ABC和△BAD中，BC = AD，请你再补充一个条件，使△ABC≌△BAD．你补充的条件是 .
6. 已知：如图， △AEF 与△ABC中， ∠E =∠B, EF=BC.请你添加一个条件，使△AEF ≌ △ABC.
对于添加条件使两三角形全等的问题，当已有两个条件（包括隐含条件）时，如何思考？
7.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
（1）当直线MN旋转到如图(1)所示的位置时,猜想线段AD、BE、DE的数量关系，并证明你的猜想。
（2）当直线MN旋转到图(2)的位置时,猜想线段AD,BE,DE的数量关系，并证明你的猜想
（3）当直线MN旋转到图(3)的位置时,猜想线段AD,BE,DE的数量关系，并证明你的猜想