人教版八年级上册11.1.3 三角形的稳定性课文配套课件ppt

这是一份人教版八年级上册11.1.3 三角形的稳定性课文配套课件ppt，共16页。PPT课件主要包含了△AED，△AFD，或10等内容，欢迎下载使用。

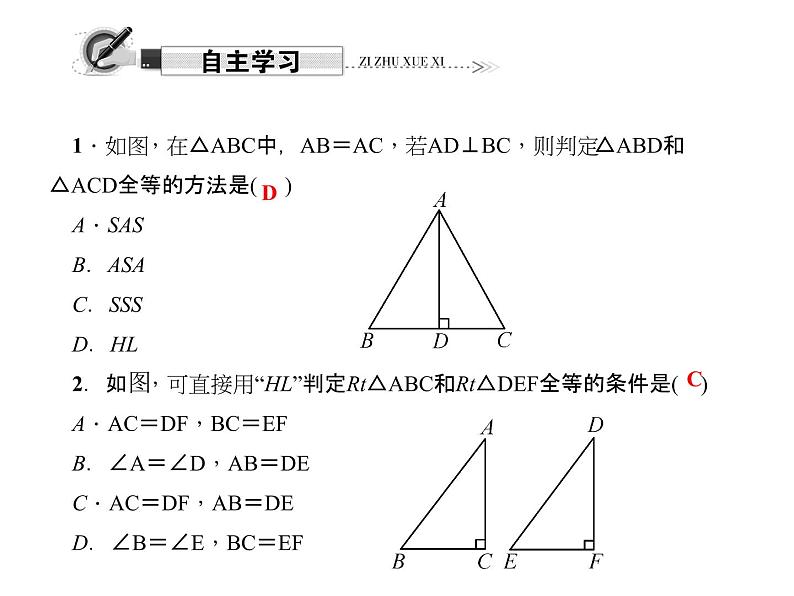
1．如图，在△ABC中，AB＝AC，若AD⊥BC，则判定△ABD和△ACD全等的方法是( )A．SAS B．ASA C．SSS D．HL2．如图，可直接用“HL”判定Rt△ABC和Rt△DEF全等的条件是( )A．AC＝DF，BC＝EF B．∠A＝∠D，AB＝DEC．AC＝DF，AB＝DE D．∠B＝∠E，BC＝EF
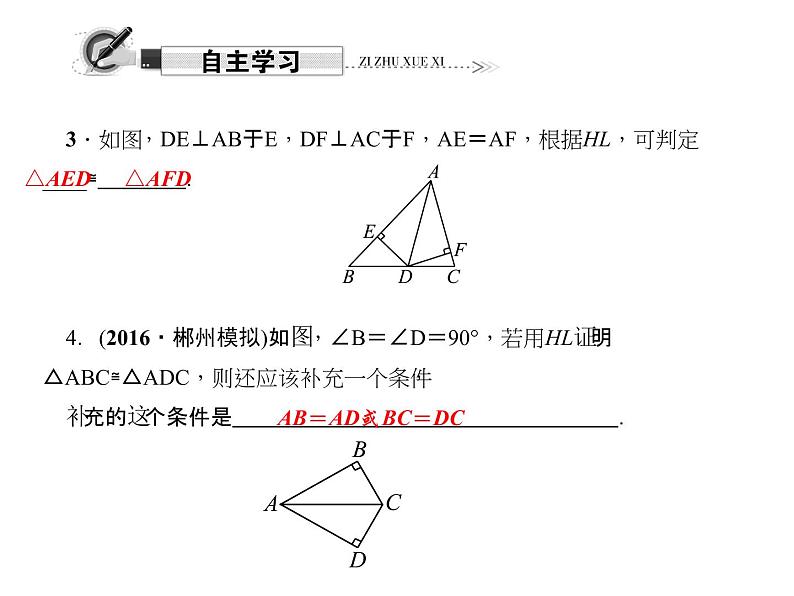
3．如图，DE⊥AB于E，DF⊥AC于F，AE＝AF，根据HL，可判定____≌ ．4．(2016·郴州模拟)如图，∠B＝∠D＝90°，若用HL证明△ABC≌△ADC，则还应该补充一个条件，补充的这个条件是 ．
AB＝AD或BC＝DC
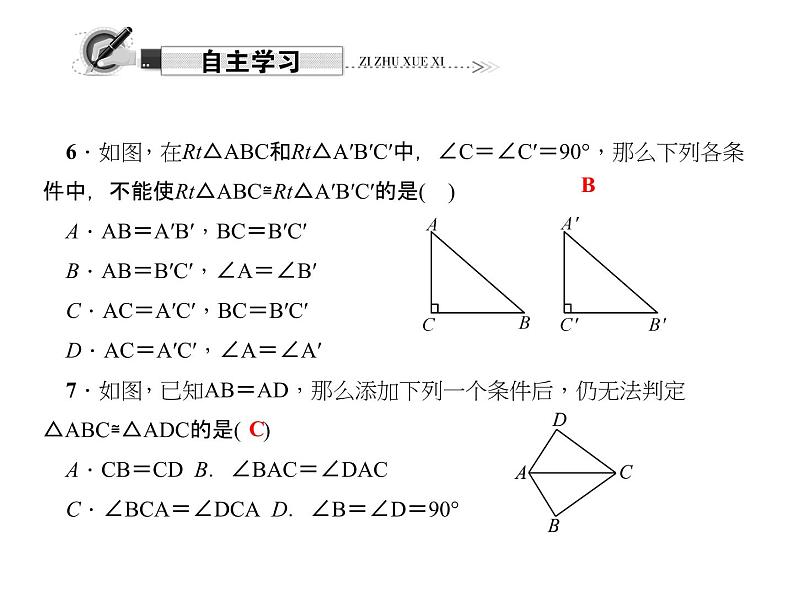
6．如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，那么下列各条件中，不能使Rt△ABC≌Rt△A′B′C′的是( )A．AB＝A′B′，BC＝B′C′B．AB＝B′C′，∠A＝∠B′C．AC＝A′C′，BC＝B′C′D．AC＝A′C′，∠A＝∠A′7．如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是( )A．CB＝CD B．∠BAC＝∠DACC．∠BCA＝∠DCA D．∠B＝∠D＝90°
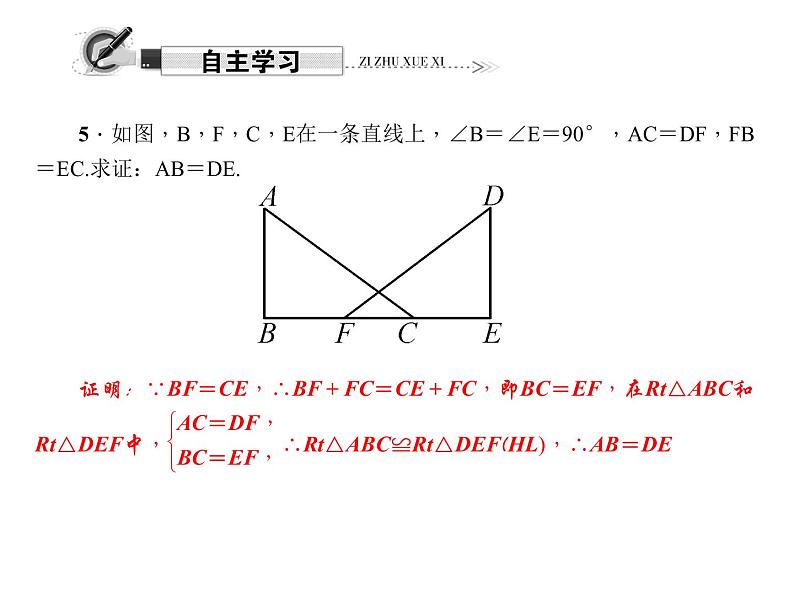
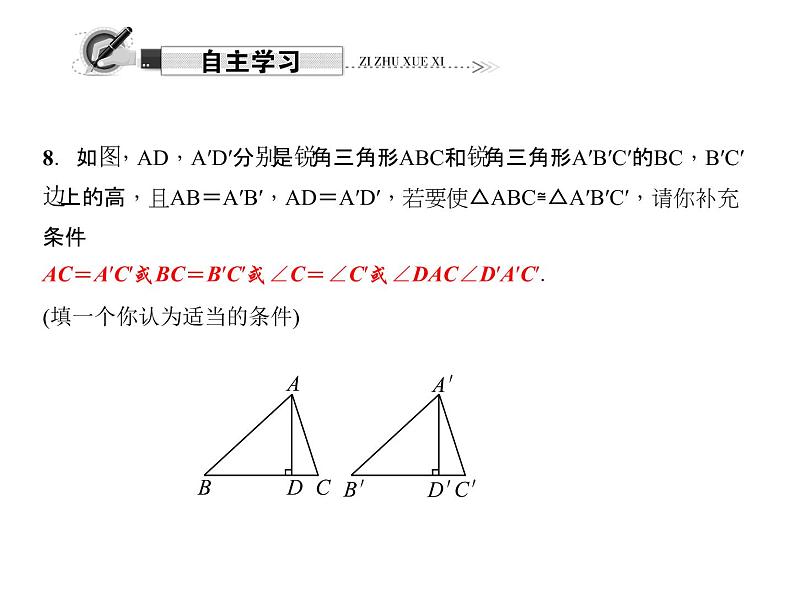
8．如图，AD，A′D′分别是锐角三角形ABC和锐角三角形A′B′C′的BC，B′C′边上的高，且AB＝A′B′，AD＝A′D′，若要使△ABC≌△A′B′C′，请你补充条件AC＝A′C′或BC＝B′C′或∠C＝∠C′或∠DAC∠D′A′C′．(填一个你认为适当的条件)
9．如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，BE＝CF.(1)图中有几对全等的三角形？请一一列出；(2)选择一对你认为全等的三角形进行证明．
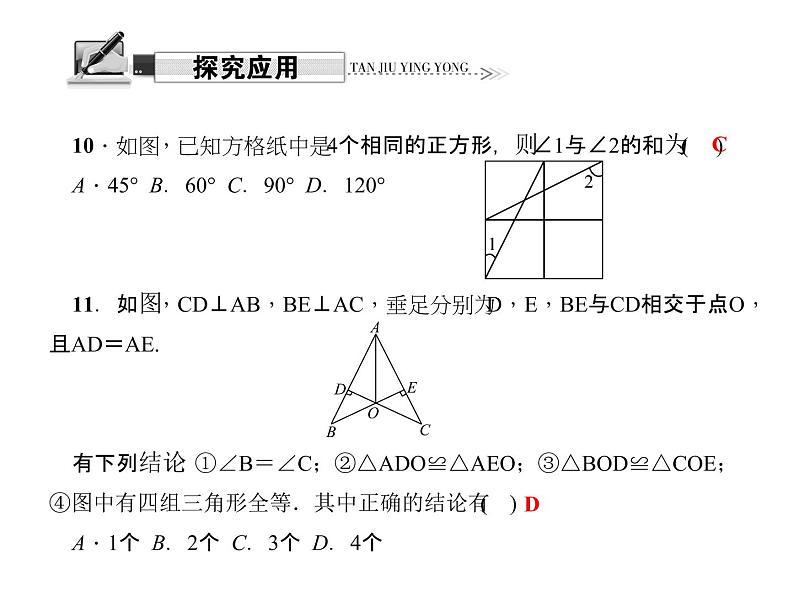
10．如图，已知方格纸中是4个相同的正方形，则∠1与∠2的和为( )A．45° B．60° C．90° D．120°11．如图，CD⊥AB，BE⊥AC，垂足分别为D，E，BE与CD相交于点O，且AD＝AE.有下列结论：①∠B＝∠C；②△ADO≌△AEO；③△BOD≌△COE；④图中有四组三角形全等．其中正确的结论有( )A．1个 B．2个 C．3个 D．4个
12．如图，在Rt△ABC中，∠C＝90°，AC＝10，BC＝5，线段PQ＝AB，PQ两点分别在AC和过点A且垂直于AC的射线AO上运动，当AP＝ 时，△ABC和△PQA全等．
13．如图，在△ABC中，AD是中线，分别过点B，C作AD及其延长线的垂线BE，CF，垂足分别为点E，F.求证：BE＝CF.证明：∵在△ABC中，AD是中线，∴BD＝CD，∵CF⊥AD，BE⊥AD，∴∠CFD＝∠BED＝90°，在△BED与△CFD中，∠BED＝∠CFD，∠BDE＝∠CDF，BD＝CD，∴△BED≌△CFD，∴BE＝CF
14．如图，在△ABC中，∠BAC＝90°，AB＝AC，D在AC上，E在BA的延长线上，BD＝CE，BD的延长线交CE于F，求证：BF⊥CE.证明：∵BD＝CE，AB＝AC，∴Rt△BAD≌Rt△CAE(HL)，∴∠ADB＝∠E，∵∠BAC＝90°，∴∠EBF＋∠ADB＝90°，∴∠EBF＋∠E＝90°，∴∠BFE＝90°，即BF⊥CE
15．如图，在△ABD和△ACE中，F，G分别是AC和DB，AB和EC的交点，现有如下4个论断：①AB＝AC；②AD＝AE；③AF＝AG；④AD⊥BD，AE⊥CE.以其中3个论断为题设，填入下面的已知栏中，剩余一个论断为结论，填入下面的求证栏中，组成一个真命题，并写出证明过程．
已知：AD＝AE，AF＝AG，AD⊥BD，AE⊥CE求证：AB＝AC证明：∵AD⊥BD，AE⊥CE，∴∠D＝∠E＝90°，又∵AD＝AE，AF＝AG，∴Rt△ADF≌Rt△AEG，∴∠DAF＝∠EAG，∴∠DAF＋∠BAC＝∠EAG＋∠BAC，即∠BAD＝∠CAE，∴△ABD≌△ACE(ASA)，∴AB＝AC
16．已知点O到△ABC的两边AB，AC所在直线的距离相等，且OB＝OC.(1)如图①，若点O在边BC上，求证：∠ABO＝∠ACO；(2)如图②，若点O在△ABC的内部，求证：∠ABO＝∠ACO.
证明：(1)过点O分别作OE⊥AB，OF⊥AC，E，F分别是垂足，由题意知，OE＝OF，OB＝OC，∴Rt△OEB≌Rt△OFC(HL)，∴∠ABO＝∠ACO(2)过点O分别作OE⊥AB，OF⊥AC，E，F分别是垂足，由题意知，OE＝OF，在Rt△OEB和Rt△OFC中，∵OE＝OF，OB＝OC，∴Rt△OEB≌Rt△OFC(HL)，∴∠OBE＝∠OCF.过O作OH⊥BC于H，由HL可证Rt△OBH≌Rt△OCH，∴∠OBH＝∠OCH，∴∠OBH＋∠OBE＝∠OCH＋∠OCF，即∠ABO＝∠ACO