初中数学人教版八年级上册13.3.1 等腰三角形课文ppt课件

这是一份初中数学人教版八年级上册13.3.1 等腰三角形课文ppt课件，共13页。

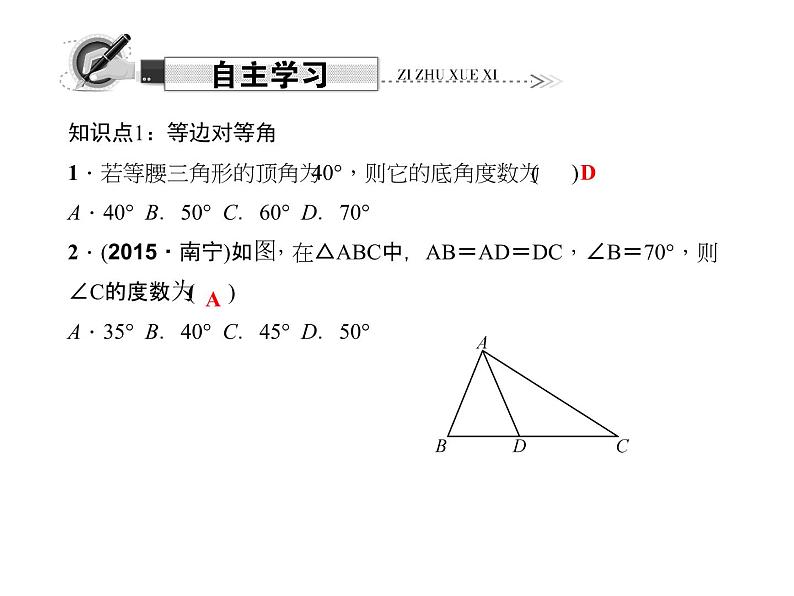
知识点1：等边对等角1．若等腰三角形的顶角为40°，则它的底角度数为( )A．40° B．50° C．60° D．70°2．(2015·南宁)如图，在△ABC中，AB＝AD＝DC，∠B＝70°，则∠C的度数为( )A．35° B．40° C．45° D．50°
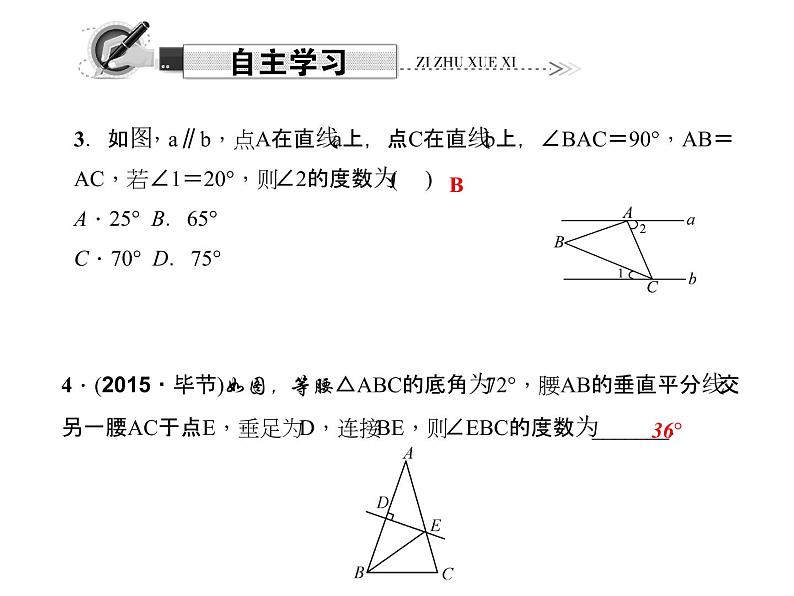
3．如图，a∥b，点A在直线a上，点C在直线b上，∠BAC＝90°，AB＝AC，若∠1＝20°，则∠2的度数为( )A．25° B．65°C．70° D．75°
4．(2015·毕节)如图，等腰△ABC的底角为72°，腰AB的垂直平分线交另一腰AC于点E，垂足为D，连接BE，则∠EBC的度数为_______．
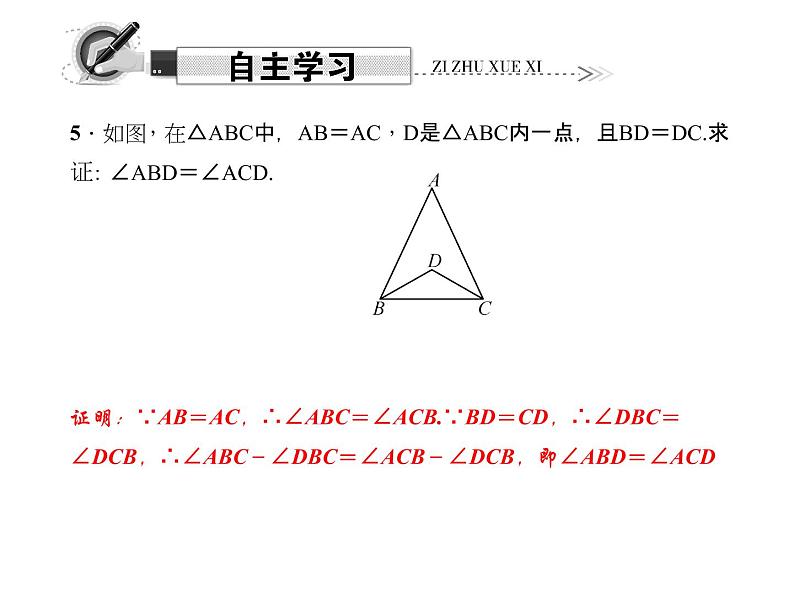
5．如图，在△ABC中，AB＝AC，D是△ABC内一点，且BD＝DC.求证：∠ABD＝∠ACD.
证明：∵AB＝AC，∴∠ABC＝∠ACB.∵BD＝CD，∴∠DBC＝∠DCB，∴∠ABC－∠DBC＝∠ACB－∠DCB，即∠ABD＝∠ACD
知识点2：三线合一6．等腰三角形是轴对称图形，它的对称轴是( )A．过顶点的直线B．底边的垂线C．顶角的角平分线所在的直线D．腰上的高所在的直线7．(2015·苏州)如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝35°，则∠C的度数为( )A．35° B．45° C．55° D．60°
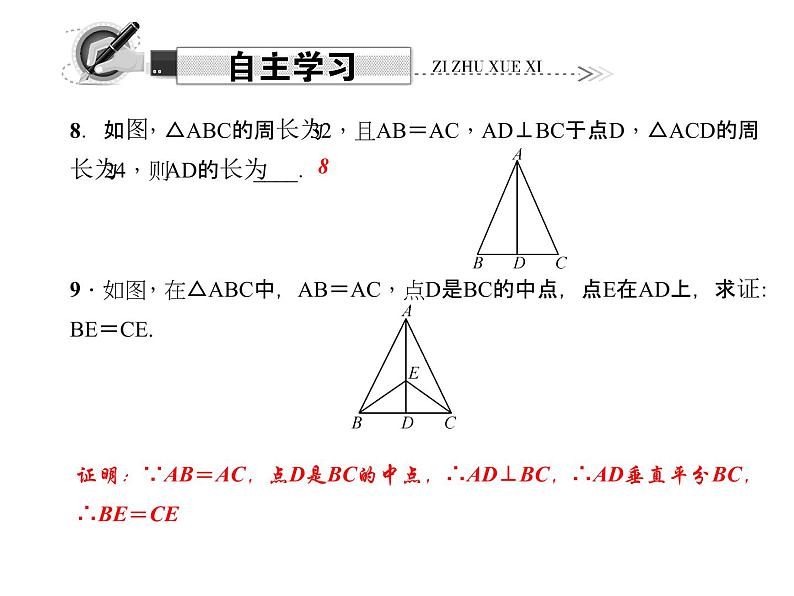
8．如图，△ABC的周长为32，且AB＝AC，AD⊥BC于点D，△ACD的周长为24，则AD的长为____．9．如图，在△ABC中，AB＝AC，点D是BC的中点，点E在AD上，求证：BE＝CE.
证明：∵AB＝AC，点D是BC的中点，∴AD⊥BC，∴AD垂直平分BC，∴BE＝CE
10．已知等腰三角形的一个内角为70°，则另外两个内角的度数为( )A．55°，55° B．70°，40°C．55°，55°或70°，40° D．以上都不对11．如图，一钢架NAM中，∠A＝15°，现要在角的内部焊上等长的钢条(相邻钢条首尾相接)来加固钢架．若AP1＝P1P2，则这样的钢条最多只能焊上( )A．4根 B．5根 C．6根 D．7根
12．如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD＝BC，AE＝AC，则∠DCE的大小为_______.13．(例题1变式)如图，在△ABC中，D在BC上，若AD＝BD，AB＝AC＝CD，求∠BAC的度数．
解：∵AD＝BD，∴∠B＝∠BAD，∵AB＝AC＝CD，∴∠B＝∠C，∠ADC＝∠DAC.设∠B＝∠BAD＝∠C＝x°，则∠ADC＝∠DAC＝2x°，在△ACD中，有2x＋2x＋x＝180，∴x＝36，∴∠BAC＝3x°＝108°
14．如图，AD是△ABC的角平分线，EF是AD的垂直平分线，交BC的延长线于点F，连接AF.求证：∠BAF＝∠ACF.
证明：∵EF是AD的垂直平分线，∴AF＝DF，∴∠FAD＝∠ADF.∵AD是∠BAC的平分线，∴∠DAB＝∠CAD.∵∠FAD＝∠FAC＋∠CAD，∠ADF＝∠B＋∠DAB，∴∠FAC＝∠B，∴∠BAC＋∠FAC＝∠B＋∠BAC，即∠BAF＝∠ACF
15．(习题6变式)如图，点D，E在△ABC的边BC上，连接AD，AE.有下列论断：①AB＝AC；②AD＝AE；③BD＝CE.以其中两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②⇒③；①③⇒②；②③⇒①.(1)以上三个命题是真命题的为__________________________________．(2)请选择一个真命题进行证明(先写出所选命题，然后证明)．
①②⇒③，①③⇒②，②③⇒①
解：(2)若选①②⇒③，证法如下：过点A作AM⊥BC于M，∵AB＝AC，AM⊥BC，∴BM＝CM，∵AD＝AE，AM⊥BC，∴DM＝EM，∴BM－DM＝CM－EM，即BD＝CE.另两种选法可由证三角形全等而得
16．如图，在等腰三角形ABC中，AB＝AC，点D在BC上，且AD＝AE.(1)若∠BAC＝90°，∠BAD＝30°，求∠EDC的度数；(2)若∠BAC＝α(α>30°)，∠BAD＝30°，求∠EDC的度数；(3)猜想∠EDC与∠BAD的数量关系．(不必证明)