2018-2019学年广东省广州市天河区广州市第一一三中学九上期中数学试卷

这是一份2018-2019学年广东省广州市天河区广州市第一一三中学九上期中数学试卷，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 方程 x2=4x 的解是
A. x=4B. x=2C. x=4 或 x=0D. x=0

2. 观察下列银行标志，从图案看既是轴对称图形又是中心对称图形的有
A. 1 个B. 2 个C. 3 个D. 4 个

3. 若关于 x 的一元二次方程 x2+x−3m=0 有两个不相等的实数根，则 m 的取值范围是
A. m>112B. m<112C. m>−112D. m<−112

4. 若抛物线 y=m+1xm2−2 的开口向上，则 m 的值为
A. 2B. −2C. ±2D. 1

5. 如图，⊙O 的直径为 10，圆心 O 到弦 AB 的距离 OM 的长为 3，则弦 AB 的长是
A. 4B. 6C. 7D. 8

6. 如图，点 A，B，C，D，O 都在方格纸的格点上，若 △COD 是由 △AOB 绕点 O 逆时针方向旋转而得，则旋转的角度为
A. 30∘B. 90∘C. 45∘D. 135∘

7. 用配方法解方程 x2−2x−5=0 时，原方程应变形为
A. x+12=6B. x+22=9C. x−12=6D. x−22=9

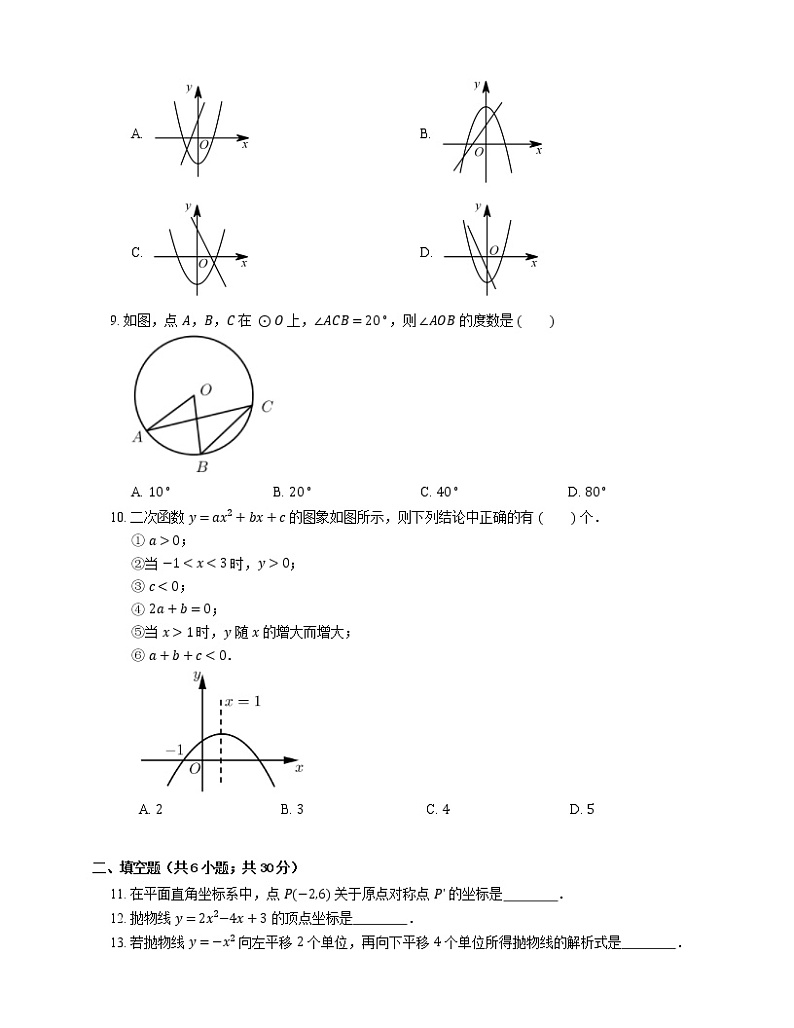
8. 在同一坐标系中，一次函数 y=ax+2 与二次函数 y=x2+a 的图象可能是
A. B.
C. D.

9. 如图，点 A，B，C 在 ⊙O 上，∠ACB=20∘，则 ∠AOB 的度数是
A. 10∘B. 20∘C. 40∘D. 80∘

10. 二次函数 y=ax2+bx+c 的图象如图所示，则下列结论中正确的有 个．
① a>0；
②当 −10；
③ c<0；
④ 2a+b=0；
⑤当 x>1 时，y 随 x 的增大而增大；
⑥ a+b+c<0．
A. 2B. 3C. 4D. 5

二、填空题（共6小题；共30分）
11. 在平面直角坐标系中，点 P−2,6 关于原点对称点 Pʹ 的坐标是 ．

12. 抛物线 y=2x2−4x+3 的顶点坐标是 ．

13. 若抛物线 y=−x2 向左平移 2 个单位，再向下平移 4 个单位所得抛物线的解析式是 ．

14. 已知 ⊙O 的直径是 6，圆心 O 到直线 l 的距离是 3，则直线 l 与 ⊙O 的位置关系是 ．

15. 已知 3 是一元二次方程 x2−4x+c=0 的一个根，则另一根为 ．

16. 圆的一条弦长等于它的半径，那么这条弦所对圆心角的度数是 ．

三、解答题（共9小题；共117分）
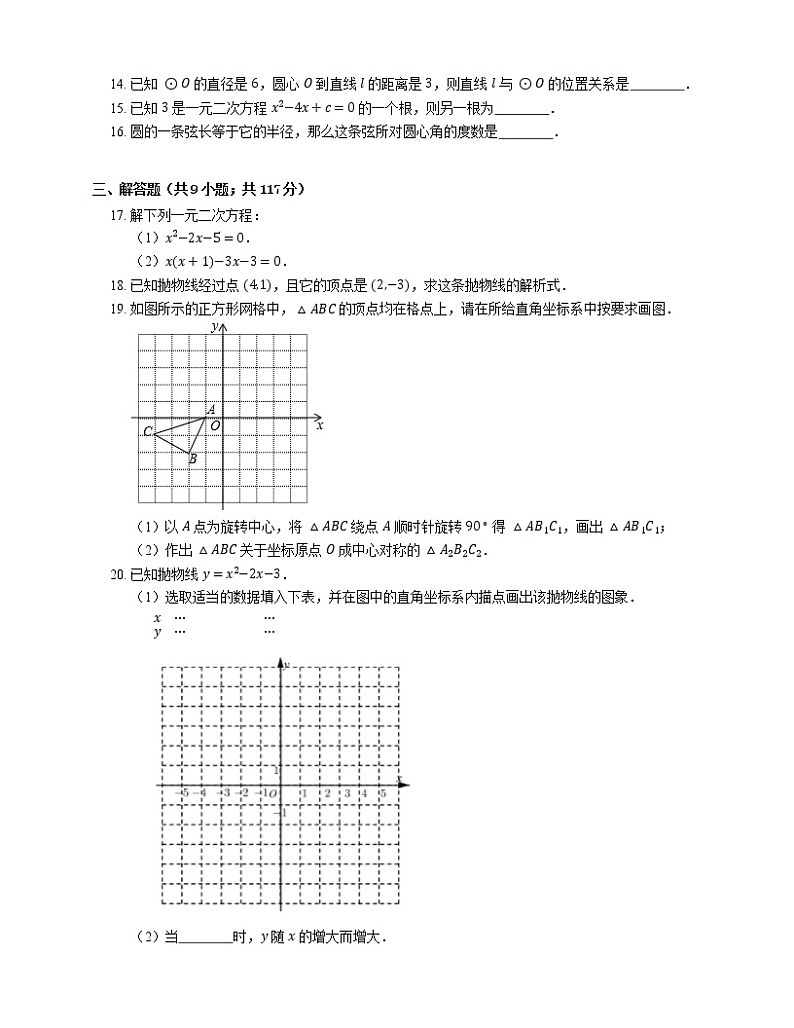
17. 解下列一元二次方程：
（1）x2−2x−5=0．
（2）xx+1−3x−3=0．

18. 已知抛物线经过点 4,1，且它的顶点是 2,−3，求这条抛物线的解析式．

19. 如图所示的正方形网格中，△ABC 的顶点均在格点上，请在所给直角坐标系中按要求画图．
（1）以 A 点为旋转中心，将 △ABC 绕点 A 顺时针旋转 90∘ 得 △AB1C1，画出 △AB1C1；
（2）作出 △ABC 关于坐标原点 O 成中心对称的 △A2B2C2．

20. 已知抛物线 y=x2−2x−3．
（1）选取适当的数据填入下表，并在图中的直角坐标系内描点画出该抛物线的图象．
x⋯⋯y⋯⋯

（2）当 时，y 随 x 的增大而增大．
（3）当 时，y<0．
（4）求抛物线与 x 轴的交点坐标、与 y 轴的交点坐标，并求此三个交点所构成的三角形的面积．

21. 如图：水平放置的圆柱形排水管道内，水面的宽度 AB=103 cm，水面的最大深度为 5 cm，求排水管道截面圆形的半径．

22. 已知抛物线 y=x2+2mx−54m2m>0．
（1）求证：该抛物线与 x 轴必有两个交点．
（2）若抛物线与 x 轴的两个交点分别为 A，B（点 A 在点 B 的左侧），且 AB=6，求 m 的值．

23. 现在全社会对空气污染问题越来越重视，空气净化器的销量也大增，商场从厂家购进了A、B两种型号的空气净化器，已知一台A型空气净化器的进价比一台B型空气净化器的进价多 300 元，用 7500 元购进A型空气净化器和用 6000 元购进B型空气净化器的台数相同．
（1）求一台B型空气净化器的进价为多少元?
（2）在销售过程中，A型空气净化器因为净化能力强，嗓音小而更受消费者的欢迎，为了增大B型空气净化器的销量，商场决定对B型空气净化器进行降价销售．经市场调查，当B型空气净化器的售价为 1800 元时，每天可卖出 4 台，在此基础上，售价每降低 50 元，每天多卖出 1 台，如果每天商场销售B型空气净化器的利润为 3200 元，请问商场应将B型空气净化器的售价定为多少元?

24. 探究：
（1）如图 1，在正方形 ABCD 中，E，F 分别是 BC，CD 上的点，且 ∠EAF=45∘，试判断 BE，DF 与 EF 三条线段之间的数量关系，直接写出判断结果： ．
（2）如图 2，若把（1）问中的条件变为“在四边形 ABCD 中，AB=AD，∠B+∠D=180∘，E，F 分别是边 BC，CD 上的点，且 ∠EAF=12∠BAD”，则（1）问中的结论是否仍然成立?若成立，请给出证明；若不成立，请说明理由．
（3）在（2）问中，若将 △AEF 绕点 A 逆时针旋转，当点分别 E，F 运动到 BC，CD 延长线上时，如图 3 所示，其它条件不变，则（1）问中的结论是否发生变化?若变化，请给出结论并予以证明．

25. 如图，在坐标系中，矩形 ABCD 的两个顶点 B1,0，C3,0，以 A 为顶点的抛物线 y=−x2+2x+m 过点 C，动点 P 从点 A 出发，沿线段 AB 向点 B 运动，同时动点 Q 从点 C 出发，沿线段 CD 向点 D 运动，点 P，Q 的运动速度均为每秒 1 个单位，运动时间为 t 秒，过点 P 作 PE⊥AB 交 AC 于点 E．
（1）求抛物线的解析式．
（2）过点 E 作 EF⊥AD 于 F，交抛物线于点 G，当 t 为何值时，△ACG 的边 AC 上的高最大?最大值为多少?
（3）在动点 P，Q 运动的过程中，当 t 为何值时，在矩形 ABCD 内（包括边界）存在点 H，使以 C，Q，E，H 为顶点的四边形为菱形?请直接写出 t 的值．
答案
第一部分
1. C
2. B
3. C
4. A
5. D
6. B
7. C
8. C
9. C
10. A
第二部分
11. 2,−6
12. 1,1
13. y=−x+22−4
14. 相切
15. 1
16. 60∘
第三部分
17. （1） x1=1+6，x2=1−6．
（2） x1=−1，x2=3．
18. y=x−22−3．
19. （1） 如图所示．
（2） 如图所示．
20. （1） 略．
（2） x>1
（3） −1 （4） 与 x 轴交点坐标为 −1,0，3,0，与 y 轴交点坐标为 0,−3，面积为 6．
21. 10 cm．
22. （1） 略
（2） 2
23. （1） 每台B型空气净化器的进价为 1200 元．
（2） 电器商社应将B型空气净化器的售价定为 1600 元．
24. （1） EF=BE+DF
（2） 结论 EF=BE+DF 仍然成立．
（3） EF，BE，DF 之间的关系是 EF=BE−DF．
25. （1） y=−x2+2x+3．
（2） t=2 时，△ACG 边 AC 上的高最大，最大值为 55．
（3） t=20−85 或 t=2013 时，以 C，Q，E，H 为顶点的四边形为菱形．