



2021学年24.1.1 圆说课ppt课件
展开掌握与圆切线有关模型的证明方法,并理解其基本思路.运用与圆切线有关模型解决相关证明和计算问题.
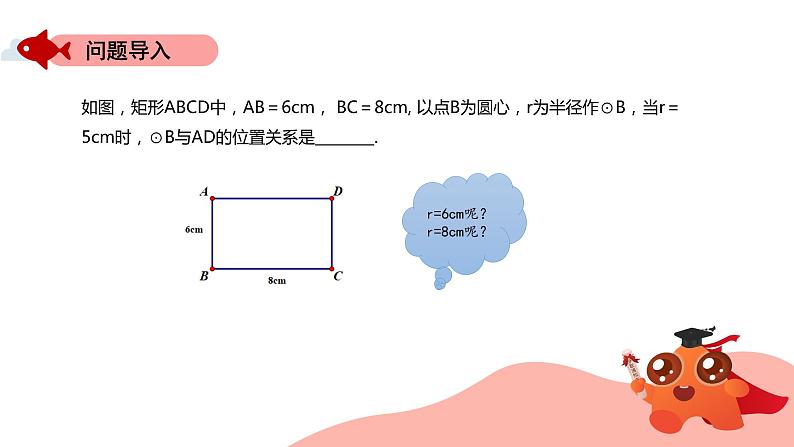
如图,矩形ABCD中,AB=6cm, BC=8cm, 以点B为圆心,r为半径作⊙B,当r=5cm时,⊙B与AD的位置关系是________.
r=6cm呢? r=8cm呢?
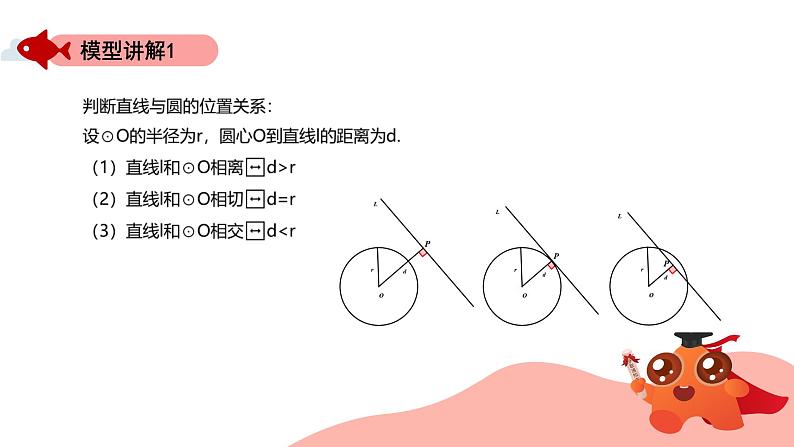
关键点:有交点,作垂直,证半径.
方法:①过圆心向已知直线作垂线;②证得垂线段的长度等于已知圆的半径.
类型:圆与直线无公共点
关键点:有交点,连半径,证垂直.
方法:①过圆心向已知公共点作半径;②证该半径与已知直线垂直.
类型:圆与直线有公共点
有交点,连半径,证垂直.
无交点,作垂直,证半径.
1.如图,已知Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,以2.4为半径画圆,AB是⊙C的切线吗?
2.如图,△ABC中,AB=AC,D是BC边的中点,以点D为圆心的圆与AB相切于点E.求证:AC与⊙D相切.
3.如图,AB是⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E.连接DF.(1)试判断直线DE与⊙O的位置关系,并说明理由;(2)若⊙O的半径为2,∠BAC=60°,求线段EF的长.
专题14 圆之切线的判定课件PPT: 这是一份专题14 圆之切线的判定课件PPT,共38页。
专题14【精品】 圆之切线的判定-2022年中考数学几何模型解题策略研究(课件+讲义): 这是一份专题14【精品】 圆之切线的判定-2022年中考数学几何模型解题策略研究(课件+讲义),文件包含专题14圆之切线的判定pptx、专题14圆之切线的判定解析版docx、专题14圆之切线的判定原卷版docx等3份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
初中数学湘教版九年级下册2.5 直线与圆的位置关系复习课件ppt: 这是一份初中数学湘教版九年级下册2.5 直线与圆的位置关系复习课件ppt,共24页。PPT课件主要包含了2016·南宁,2016·北海,切线的判定,圆周角定理,垂径定理,∵OA是⊙O的半径,BC⊥OA,∴BC为⊙O的切线,AB⊥BC,或∠ABC90˚等内容,欢迎下载使用。













