2021年高考理科数学一轮复习：专题8.1 空间几何体的结构及其表面积、体积 题型全归纳与高效训练突破

这是一份2021年高考理科数学一轮复习：专题8.1 空间几何体的结构及其表面积、体积 题型全归纳与高效训练突破，文件包含专题81空间几何体的结构及其表面积体积学生版docx、专题81空间几何体的结构及其表面积体积老师版pdf等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
目录
TOC \ "1-3" \h \u \l "_Tc16056" 一、考点全归纳 PAGEREF _Tc16056 2
\l "_Tc26528" 二 题型全归纳 PAGEREF _Tc26528 5
\l "_Tc9266" 题型一 空间几何体的几何特征 PAGEREF _Tc9266 5
\l "_Tc5451" 题型二 空间几何体的三视图 PAGEREF _Tc5451 6
\l "_Tc10118" 类型一 已知几何体，识别三视图 PAGEREF _Tc10118 6
\l "_Tc29296" 类型二 已知三视图，判断几何体 PAGEREF _Tc29296 7
\l "_Tc13903" 类型三 已知几何体的某些视图，判断其他视图 PAGEREF _Tc13903 9
\l "_Tc16524" 题型三 空间几何体的直观图 PAGEREF _Tc16524 10
\l "_Tc5434" 题型四 空间几何体的表面积 PAGEREF _Tc5434 11
\l "_Tc7726" 题型五 空间几何体的体积 PAGEREF _Tc7726 13
\l "_Tc2765" 类型一 直接利用公式求体积 PAGEREF _Tc2765 13
\l "_Tc6447" 类型二 割补法求体积 PAGEREF _Tc6447 14
\l "_Tc28988" 类型三 等体积法求体积 PAGEREF _Tc28988 15
\l "_Tc8109" 题型六 球与空间几何体的接、切问题 PAGEREF _Tc8109 15
\l "_Tc11726" 类型一 外接球 PAGEREF _Tc11726 16
\l "_Tc25350" 类型二 内切球 PAGEREF _Tc25350 17
\l "_Tc18064" 类型三 确定球心位置的三种方法 PAGEREF _Tc18064 17
\l "_Tc25805" 三、高效训练突破 PAGEREF _Tc25805 19
一、考点全归纳
1．空间几何体的结构特征
(1)多面体的结构特征
(2)旋转体的形成
2.三视图
(1)几何体的三视图包括正视图、侧视图、俯视图，分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线．
(2)三视图的画法
①基本要求：长对正，高平齐，宽相等．
②画法规则：正侧一样高，正俯一样长，侧俯一样宽；看不到的线画虚线．
3．直观图
(1)画法：常用斜二测画法．
(2)规则：①原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴，y′轴的夹角为45°(或135°)，z′轴与x′轴和y′轴所在的平面垂直；
②原图形中平行于坐标轴的线段，直观图中仍平行于坐标轴．平行于x轴和z轴的线段在直观图中保持原长度不变，平行于y轴的线段长度在直观图中变为原来的一半．
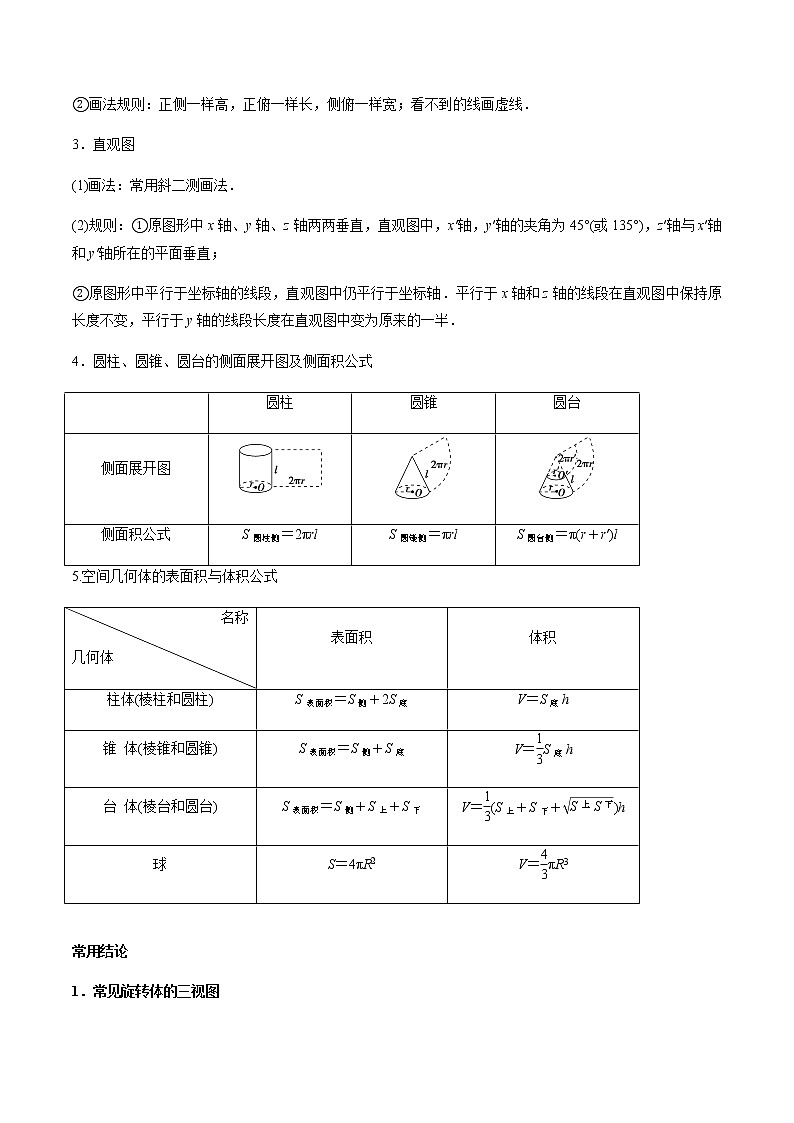
4．圆柱、圆锥、圆台的侧面展开图及侧面积公式
5.空间几何体的表面积与体积公式
常用结论
1．常见旋转体的三视图
(1)球的三视图都是半径相等的圆．
(2)水平放置的圆锥的正视图和侧视图均为全等的等腰三角形．
(3)水平放置的圆台的正视图和侧视图均为全等的等腰梯形．
(4)水平放置的圆柱的正视图和侧视图均为全等的矩形．
2．斜二测画法中的“三变”与“三不变”
“三变”eq \b\lc\{(\a\vs4\al\c1(坐标轴的夹角改变,与y轴平行的线段的长度变为原来的一半,图形改变))
“三不变”eq \b\lc\{(\a\vs4\al\c1(平行性不改变,与x，z轴平行的线段的长度不改变,相对位置不改变))
3．正方体的外接球、内切球及与各条棱相切球的半径
(1)外接球：球心是正方体的中心；半径r＝eq \f(\r(3),2)a(a为正方体的棱长)．
(2)内切球：球心是正方体的中心；半径r＝eq \f(a,2)(a为正方体的棱长)．
(3)与各条棱都相切的球：球心是正方体的中心；半径r＝eq \f(\r(2),2)a(a为正方体的棱长).
4.正四面体的外接球、内切球的球心和半径
(1)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分)．
(2)外接球：球心是正四面体的中心；半径r＝eq \f(\r(6),4)a(a为正四面体的棱长)．
(3)内切球：球心是正四面体的中心；半径r＝eq \f(\r(6),12)a(a为正四面体的棱长)．
二 题型全归纳
题型一 空间几何体的几何特征
【题型要点】解决与空间几何体结构特征有关问题的技巧
(1)关于空间几何体的结构特征辨析关键是紧扣各种空间几何体的概念，要善于通过举反例对概念进行辨析，即要说明一个命题是错误的，只需举一个反例即可．
(2)圆柱、圆锥、圆台的有关元素都集中在轴截面上，解题时要注意用好轴截面中各元素的关系．
(3)棱(圆)台是由棱(圆)锥截得的，所以在解决棱(圆)台问题时，要注意“还台为锥”的解题策略．
【例1】(2020·辽宁省鞍山一中高三上学期期末)给出下列命题：
(1)棱柱的侧棱都相等，侧面都是全等的平行四边形；
(2)若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；
(3)在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；
(4)存在每个面都是直角三角形的四面体；
(5)棱台的侧棱延长后交于一点．
其中正确命题的个数为( )
A．2 B．3 C．4 D．5
【例2】给出下列几个命题：
①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；
②底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱；
③棱台的上、下底面可以不相似，但侧棱长一定相等．
其中正确命题的个数是( )
A．0 B．1
C．2 D．3
题型二 空间几何体的三视图
【题型要点】三视图问题的常见类型及解题策略
(1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，看不到的部分用虚线表示．
(2)由几何体的部分视图画出剩余的视图．先根据已知的一部分视图，还原、推测其直观图的可能形式，然后再找其剩下部分视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．
(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为直观图．
类型一 已知几何体，识别三视图
【例1】(2020·宜宾模拟)已知棱长都为2的正三棱柱ABC­A1B1C1的直观图如图．若正三棱柱ABC­A1B1C1绕着它的一条侧棱所在直线旋转，则它的侧视图可以为( )
【例2】(2020·湖南衡阳二模)如图，正方体ABCD­A1B1C1D1的顶点A，B在平面α上，AB＝eq \r(2).若平面A1B1C1D1与平面α所成角为30°，由如图所示的俯视方向，正方体ABCD­A1B1C1D1在平面α上的俯视图的面积为( )
A．2 B．1＋eq \r(3) C．2eq \r(3) D．2eq \r(2)
类型二 已知三视图，判断几何体
【例3】如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是( )
A．三棱锥 B．三棱柱 C．四棱锥 D．四棱柱
【例4】某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为( )
A．1 B．2 C．3 D．4
类型三 已知几何体的某些视图，判断其他视图
【例5】(2020·福州模拟)如图为一圆柱切削后的几何体及其正视图，则相应的侧视图可以是( )
【例6】(2020·河北衡水中学联考)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高二丈，问：积几何？”其意思为：“今有底面为矩形的屋脊状的楔体，下底面宽3丈、长4丈，上棱长2丈，高2丈，问：它的体积是多少？”已知该楔体的正视图和俯视图如图中粗实线所示，则该楔体的侧视图的周长为( )
A．3丈 B．6丈
C．8丈 D．(5＋eq \r(13))丈
题型三 空间几何体的直观图
【题型要点】(1)斜二测画法中的“三变”与“三不变”
“三变”eq \b\lc\{(\a\vs4\al\c1(坐标轴的夹角改变,与y轴平行的线段的长度变为原来的一半,图形改变))
“三不变”eq \b\lc\{(\a\vs4\al\c1(平行性不改变,与x，z轴平行的线段的长度不改变,相对位置不改变))
(2)平面图形直观图与原图形面积间的关系
对于几何体的直观图，除掌握斜二测画法外，记住原图形面积S与直观图面积S′之间的关系S′＝eq \f(\r(2),4)S，能更快捷地进行相关问题的计算．
【例1】已知等边三角形ABC的边长为a，那么△ABC的平面直观图△A′B′C′的面积为( )
A.eq \f(\r(3),4)a2 B．eq \f(\r(3),8)a2
C.eq \f(\r(6),8)a2 D．eq \f(\r(6),16)a2
【例2】．在等腰梯形ABCD中，上底CD＝1，腰AD＝CB＝eq \r(2)，下底AB＝3，以下底所在直线为x轴，则由斜二测画法画出的直观图A′B′C′D′的面积为________．
题型四 空间几何体的表面积
【题型要点】几类空间几何体表面积的求法
(1)多面体：其表面积是各个面的面积之和．
(2)旋转体：其表面积等于侧面面积与底面面积的和．
(3)简单组合体：应搞清各构成部分，并注意重合部分的删、补．
(4)若以三视图形式给出，解题的关键是根据三视图，想象出原几何体及几何体中各元素间的位置关系及数量关系．
【例1】(2020·河南周口模拟)如图，在三棱柱ABC­A1B1C1中，AA1⊥底面ABC，AB⊥BC，AA1＝AC＝2，直线A1C与侧面AA1B1B所成的角为30°，则该三棱柱的侧面积为( )
A．4＋4eq \r(2) B．4＋4eq \r(3)
C．12 D．8＋4eq \r(2)
【例2】(2020·四川泸州一诊)在梯形ABCD中，∠ABC＝eq \f(π,2)，AD∥BC，BC＝2AD＝2AB＝2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )
A．(5＋eq \r(2))π B．(4＋eq \r(2))π
C．(5＋2eq \r(2))π D．(3＋eq \r(2))π
题型五 空间几何体的体积
【题型要点】处理体积问题的思路
①“转”：指的是转换底面与高，将原来不易求面积的底面转换为易求面积的底面，或将原来不易看出的高转换为易看出并易求解长度的高；
②“拆”：指的是将一个不规则的几何体拆成几个简单的几何体，便于计算；
③“拼”：指的是将小几何体嵌入一个大几何体中，如将一个三棱锥复原成一个三棱柱，将一个三棱柱复原成一个四棱柱，这些都是拼补的方法．
(2)求空间几何体的体积的常用方法
①公式法：对于规则几何体的体积问题，可以直接利用公式进行求解；
②割补法：把不规则的图形分割成规则的图形，然后进行体积计算；或者把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体，便于计算其体积；
③等体积法：一个几何体无论怎样转化，其体积总是不变的．如果一个几何体的底面面积和高较难求解时，我们可以采用等体积法进行求解．等体积法也称等积转化或等积变形，它是通过选择合适的底面来求几何体体积的一种方法，多用来解决有关锥体的体积，特别是三棱锥的体积．
类型一 直接利用公式求体积
【例1】(2020·山东省实验中学模拟)我国古代《九章算术》里，记载了一个“商功”的例子：今有刍童，下广二丈，袤三丈，上广三丈，袤四丈，高三丈．问积几何？其意思是：今有上下底面皆为长方形的草垛(如图所示)，下底宽2丈，长3丈，上底宽3丈，长4丈，高3丈．问它的体积是多少？该书提供的算法是：上底长的2倍与下底长的和与上底宽相乘，同样下底长的2倍与上底长的和与下底宽相乘，将两次运算结果相加，再乘以高，最后除以6.则这个问题中的刍童的体积为( )
A．13.25立方丈 B．26.5立方丈
C．53立方丈 D．106立方丈
类型二 割补法求体积
【例2】《九章算术》卷五商功中有如下问题：今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何？刍甍：底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图，设网格纸上每个小正方形的边长为1)，那么该刍甍的体积为( )
A．4 B．5 C．6 D．12
类型三 等体积法求体积
【例3】(2020·贵州部分重点中学联考)如图，在直四棱柱ABCD­A1B1C1D1中，底面ABCD是平行四边形，点E是棱BB1的中点，点F是棱CC1上靠近C1的三等分点，且三棱锥A1­AEF的体积为2，则四棱柱ABCD­A1B1C1D1的体积为( )
A．12 B．8 C．20 D．18
题型六 球与空间几何体的接、切问题
【题型要点】与球有关的切、接问题的解法
(1)旋转体的外接球：常用的解题方法是过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．
(2)多面体的外接球：常用的解题方法是将多面体还原到正方体和长方体中再去求解．
①若球面上四点P，A，B，C中PA，PB，PC两两垂直或三棱锥的三条侧棱两两垂直，可构造长方体或正方体，利用2R＝eq \r(a2＋b2＋c2)求R.
②一条侧棱垂直底面的三棱锥问题：可补形成直三棱柱．先借助几何体的几何特征确定球心位置，然后把半径放在直角三角形中求解．
(3)解题流程
类型一 外接球
【例1】已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )
A．π B．eq \f(3π,4)
C.eq \f(π,2) D．eq \f(π,4)
【例2】已知三棱锥S­ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA＝AC，SB＝BC，三棱锥S­ABC的体积为9，则球O的表面积为________．
类型二 内切球
【例3】如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切．记圆柱O1O2的体积为V1，表面积为S1，球O的体积为V2，表面积为S2，则eq \f(V1,V2)的值是__________，eq \f(S1,S2)＝________.
【例4】已知棱长为a的正四面体，则此正四面体的表面积S1与其内切球的表面积S2的比值为________．
类型三 确定球心位置的三种方法
决定球的几何要素是球心的位置和球的半径，在球与其他几何体的结合问题中，通过位置关系的分析，找出球心所在的位置是解题的关键，不妨称这个方法为球心位置分析法．
方法一 由球的定义确定球心
若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球．也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体外接球的球心．
(1)长方体或正方体的外接球的球心是其体对角线的中点；
(2)正三棱柱的外接球的球心是上、下底面中心连线的中点；
(3)直三棱柱的外接球的球心是上、下底面三角形外心连线的中点；
(4)正棱锥的外接球球心在其高上，具体位置可通过建立直角三角形运用勾股定理计算得到；
(5)若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心．
【例1】已知各顶点都在同一个球面上的正四棱柱的高为4，体积为16，则这个球的表面积是( )
A．16π B．20π
C．24π D．32π
方法二 构造长方体或正方体确定球心
(1)正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补形成长方体或正方体；
(2)同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥，可将三棱锥补形成长方体或正方体；
(3)若已知棱锥含有线面垂直关系，则可将棱锥补形成长方体或正方体；
(4)若三棱锥的三个侧面两两垂直，则可将三棱锥补形成长方体或正方体．
【例2】如图，边长为2的正方形ABCD中，点E，F分别是边AB，BC的中点，将△AED，△EBF，△FCD分别沿DE，EF，FD折起，使A，B，C三点重合于点A′，若四面体A′EFD的四个顶点在同一个球面上，则该球的半径为( )
A.eq \r(2) B．eq \f(\r(6),2) C.eq \f(\r(11),2) D．eq \f(\r(5),2)
方法三 由性质确定球心
利用球心O与截面圆圆心O′的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质，确定球心．
【例3】正三棱锥A­BCD内接于球O，且底面边长为eq \r(3)，侧棱长为2，则球O的表面积为________．

三、高效训练突破
一、选择题
1．中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是( )
2．(2020·安徽宣城二模)一个几何体的三视图如图所示，在该几何体的各个面中，面积最大面的面积是( )
A．2 B．2eq \r(2) C．2eq \r(3) D．4
3．某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为( )
A．2eq \r(17) B．2eq \r(5) C．3 D．2
4.一个几何体的三视图如图所示，图中直角三角形的直角边长均为1，则该几何体的体积为( )
A.eq \f(1,6) B．eq \f(\r(2),6) C.eq \f(\r(3),6) D．eq \f(1,2)
5．(2020·陕西彬州质检)一个几何体的三视图如图所示，其中正视图中△ABC是边长为1的等边三角形，俯视图为正六边形，那么该几何体的侧视图的面积为( )
A.eq \f(3,8) B．eq \f(3,4) C．1 D．eq \f(3,2)
6．(2020·江西省名校学术联盟质检)如图所示，边长为1的正方形网格中粗线画出的是某几何体的三视图，则该几何体所有棱长组成的集合为( )
A．{1，eq \r(5)} B．{1，eq \r(6)}
C．{1，eq \r(2)，eq \r(5)} D．{1，eq \r(2)，2eq \r(2)，eq \r(6)}
7．(2020·河南非凡联盟4月联考)某组合体的正视图和侧视图如图(1)所示，它的俯视图的直观图是图(2)中粗线所表示的平面图形，其中四边形O′A′B′C′为平行四边形，D′为C′B′的中点，则图(2)中平行四边形O′A′B′C′的面积为( )
A．12 B．3eq \r(2) C．6eq \r(2) D．6
8．(2020·安徽黄山一模)如图所示为某几何体的三视图，则几何体的体积为( )
A.eq \f(1,2) B．1 C.eq \f(3,2) D．3
9．(2020·湖南永州三模)某几何体的三视图如图所示，则该几何体的体积为( )
A.eq \f(5π,3) B．eq \f(4π,3) C.eq \f(π,3) D．eq \f(2π,3)
10．(2020·广东茂名一模)在长方体ABCD­A1B1C1D1中，四边形ABCD是边长为2的正方形，D1B与DC所成的角是60°，则长方体的外接球的表面积是( )
A．16π B．8π
C．4π D．4eq \r(2)π
11．(2020·江西萍乡一模)如图，网格纸上小正方形的边长为1，粗线画的是某几何体的三视图，则该几何体的体积为( )
A.eq \f(23,6) B．eq \f(7,2) C.eq \f(7,6) D．4
12．(2020·福建厦门外国语学校模拟)已知等腰直角三角形ABC中，∠ACB＝90°，斜边AB＝2，点D是斜边AB上一点(不同于点A，B)．沿线段CD折起形成一个三棱锥A­CDB，则三棱锥A­CDB体积的最大值是( )
A．1 B．eq \f(1,2) C.eq \f(1,3) D．eq \f(1,6)
二、填空题
1．一个圆台上、下底面的半径分别为3 cm和8 cm，若两底面圆心的连线长为12 cm，则这个圆台的母线长为______cm.
2．已知正四棱锥V­ABCD中，底面面积为16，一条侧棱的长为2eq \r(11)，则该棱锥的高为________．
3．某几何体的正视图和侧视图如图(1)，它的俯视图的直观图是矩形O1A1B1C1，如图(2)，其中O1A1＝6，O1C1＝2，则该几何体的侧面积为________．
4．(2019·高考全国卷Ⅱ)中国有悠久的金石文化，印信是金石文化的代表之一，印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1)．半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1，则该半正多面体共有________个面，其棱长为________．
5.已知圆锥SO，过SO的中点P作平行于圆锥底面的截面，以截面为上底面作圆柱PO，圆柱的下底面落在圆锥的底面上(如图)，则圆柱PO的体积与圆锥SO的体积的比值为________．
6．已知正三棱锥的高为1，底面边长为2eq \r(3)，内有一个球与四个面都相切，则棱锥的内切球的半径为________．
7.如图所示，已知三棱柱ABC­A1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥B1­ABC1的体积为________．
8．已知半球O的半径r＝2，正三棱柱ABC­A1B1C1内接于半球O，其中底面ABC在半球O的大圆面内，点A1，B1，C1在半球O的球面上．若正三棱柱ABC­A1B1C1的侧面积为6eq \r(3)，则其侧棱的长是________．
9.如图，正方体ABCD­A1B1C1D1的棱长为1，P为BC边的中点，Q为线段CC1上的动点，过点A，P，Q的平面截正方体所得的截面为S，当CQ＝1时，S的面积为________．
10．已知圆锥的顶点为S，母线SA，SB所成角的余弦值为eq \f(7,8)，SA与圆锥底面所成角为45°.若△SAB的面积为5eq \r(15)，则该圆锥的侧面积为________．
三 解答题
1．已知一个几何体的三视图如图所示．
(1)求此几何体的表面积；
(2)如果点P，Q在正视图中所示位置，P为所在线段的中点，Q为顶点，求在几何体表面上，从P点到Q点的最短路径的长．
2.如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.
(1)证明：平面AEC⊥平面BED；
(2)若∠ABC＝120°，AE⊥EC，三棱锥E­ACD的体积为eq \f(\r(6),3)，求该三棱锥的侧面积．
多面体
结构特征
棱柱
有两个面互相平行，其余各面都是四边形且每相邻两个四边形的公共边都互相平行
棱锥
有一个面是多边形，而其余各面都是有一个公共顶点的三角形
棱台
棱锥被平行于底面的平面所截，截面和底面之间的部分叫做棱台
几何体
旋转图形
旋转轴
圆柱
矩形
矩形一边所在的直线
或对边中点连线所在直线
圆锥
直角三角形或等腰三角形
一直角边所在的直线或等腰
三角形底边上的高所在直线
圆台
直角梯形或等腰梯形
直角腰所在的直线或
等腰梯形上下底中点
连线所在直线
球
半圆或圆
直径所在的直线
圆柱
圆锥
圆台
侧面展开图
侧面积公式
S圆柱侧＝2πrl
S圆锥侧＝πrl
S圆台侧＝π(r＋r′)l
名称
几何体
表面积
体积
柱体(棱柱和圆柱)
S表面积＝S侧＋2S底
V＝S底h
锥 体(棱锥和圆锥)
S表面积＝S侧＋S底
V＝eq \f(1,3)S底h
台 体(棱台和圆台)
S表面积＝S侧＋S上＋S下
V＝eq \f(1,3)(S上＋S下＋eq \r(S上S下))h
球
S＝4πR2
V＝eq \f(4,3)πR3