华师大版九年级上册第23章 图形的相似23.3 相似三角形1. 相似三角形示范课ppt课件

这是一份华师大版九年级上册第23章 图形的相似23.3 相似三角形1. 相似三角形示范课ppt课件，共24页。PPT课件主要包含了拓展提高等内容，欢迎下载使用。

对应角相等，对应边的比相等的两个多边形为相似多边形.
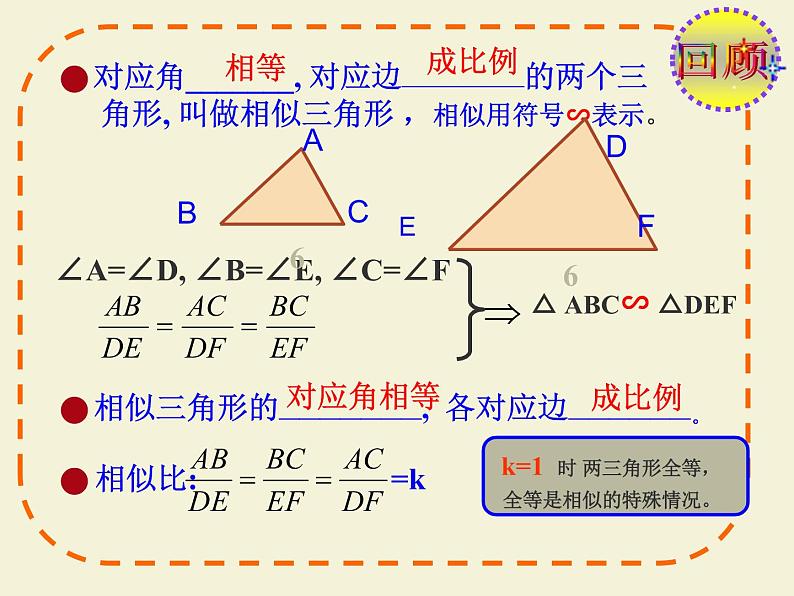
 对应角_______, 对应边——————的两个三 角形, 叫做相似三角形 ，相似用符号∽表示。
 相似三角形的———————, 各对应边——————。
∠A=∠D, ∠B=∠E, ∠C=∠F
△ ABC∽ △DEF
 相似比: =k
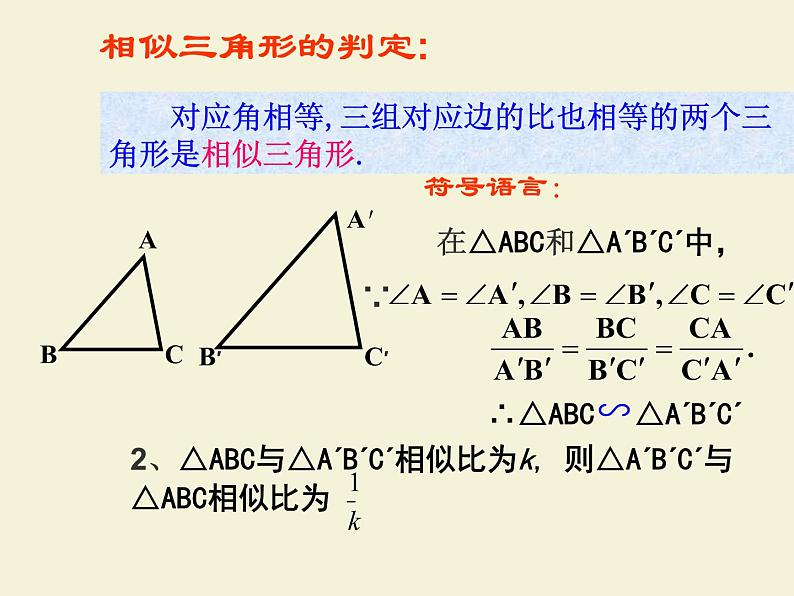
对应角相等,三组对应边的比也相等的两个三角形是相似三角形.
2、△ABC与△A´B´C´相似比为k, 则△A´B´C´与△ABC相似比为
∴△ABC∽△A´B´C´
在△ABC和△A´B´C´中，
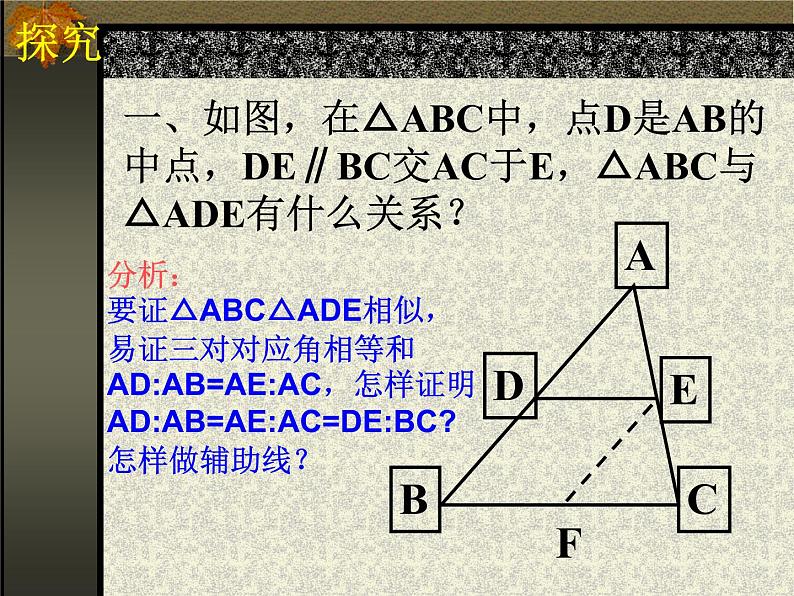
一、如图，在△ABC中，点D是AB的中点，DE∥BC交AC于E，△ABC与△ADE有什么关系？
分析：要证△ABC△ADE相似，易证三对对应角相等和AD:AB=AE:AC，怎样证明AD:AB=AE:AC=DE:BC?怎样做辅助线？
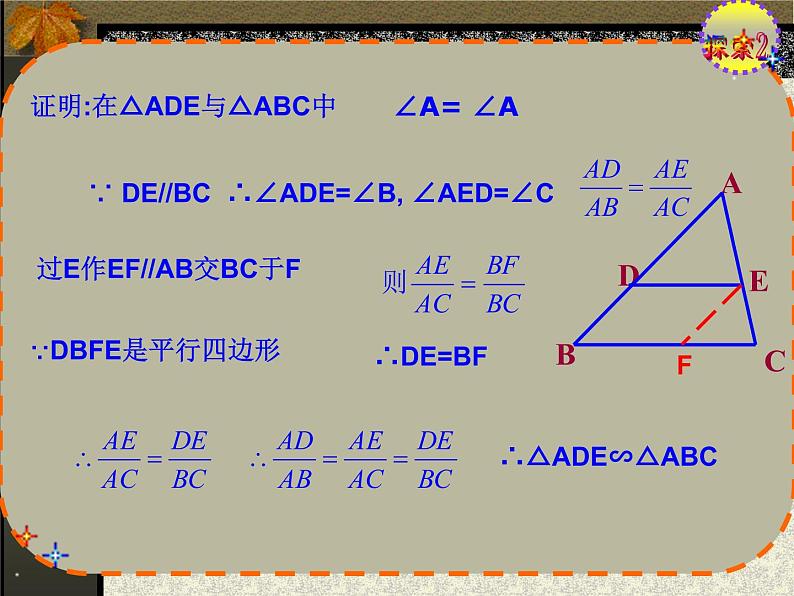
证明:在△ADE与△ABC中
∴∠ADE=∠B, ∠AED=∠C
过E作EF//AB交BC于F
∵DBFE是平行四边形
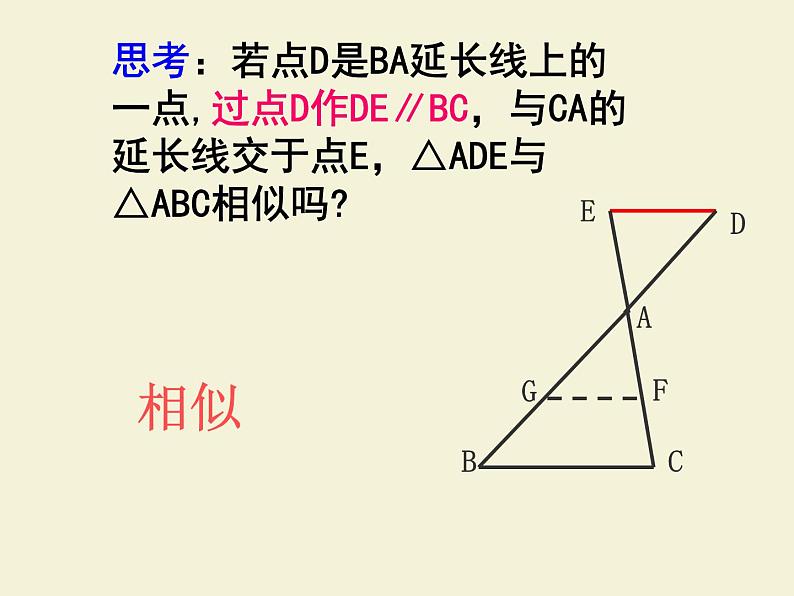
思考：若点D是BA延长线上的一点,过点D作DE∥BC，与CA的延长线交于点E，△ADE与△ABC相似吗?
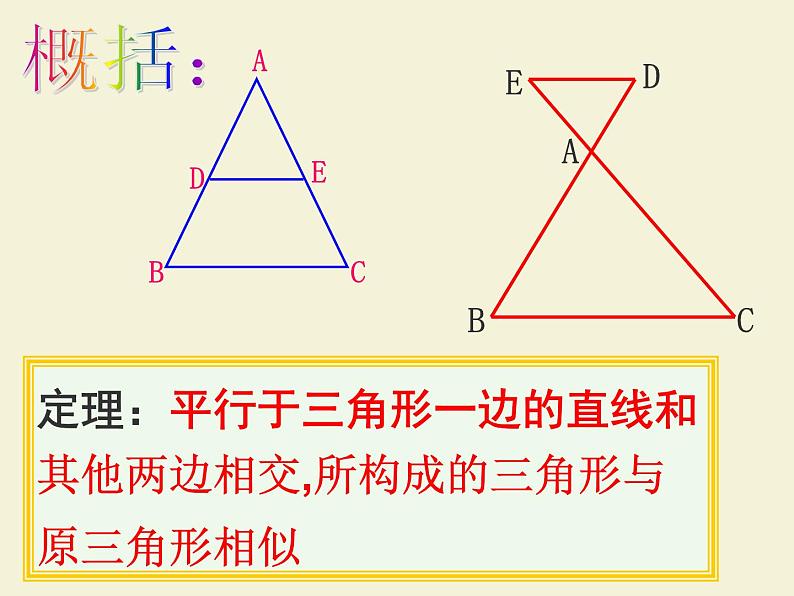
定理：平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
相似三角形的预备定理：
平行于三角形一边的直线，和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。
判定三角形相似的预备定理：（简称：平行线法）
在△ABC中， ∵ DE∥BC
1、如图,已知EF∥CD∥AB，请尽可能多地找出图中的相似三角形，并说明理由。
三角形相似具有传递性!
这是两个极具代表性的相似三角形基本模型：“A”型和“X” 型
这个两个模型在今后学习的过程中作用很大,你可要认真噢！
如图，在△ABC中，DG∥EH∥FI∥BC，（1）请找出图中所有的相似三角形；（2）如果AD=1，DB=3，那么DG：BC=_____。
△ADG∽△AEH∽△AFI∽△ABC
例1：如图 已知D点是AB边的三等分点，DE∥BC,DE=5，求BC的长。
分析：求BC的长，可以利用三角形相似的性质，利用条件能证两个三角形相似吗？
1、若 BF=3,CF=2,AD=1.5,DF=6,你能求出线段AE的长度吗？
∵DE∥BC,DF∥AC
∴四边形DFCE为平行四边形
∴FC=DE=2，EC=DF=6
∴AE=AC-CE=10-6=4
1、如图，在 ABCD中，E是边BC上的一点，且BE:EC=3:2，连接AE、BD交于点F，则BE:AD=_____，BF:FD=_____。
2、如图，在△ABC中，∠C的平分线交AB于D，过点D作DE∥BC交AC于E，若AD:DB=3:2，则EC:BC=______。
3、如图，DE∥BC，（1）如果AD=2，DB=3，求DE:BC的值；（2）如果AD=8，DB=12，AC=15，DE=7，求AE和BC的长．
4、如图，在□ABCD中，EF∥AB，DE:EA=2:3，EF=4，求CD的长．
如图：在△ABC中，点M是BC上任一点， MD∥AC，ME∥AB， 若 求 的值。
平行于三角形一边的直线和其他两边(或两边延长线)相交，所构成的三角形与原三角形相似。