北师大版八年级上册3 平行线的判定评优课课件ppt

这是一份北师大版八年级上册3 平行线的判定评优课课件ppt，文件包含73《平行线的判定》课件pptx、73《平行线的判定》同步练习doc、73《平行线的判定》教学设计教案doc等3份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

1、能够熟练地识别内错角、同位角、同旁内角.2、学会用平行线的三种判定定理解决问题.3、经历平行线判定定理的推导过程，了解推理、证明的方法步骤和格式。
教学重点： 掌握平行线的三种判定方法与,能够根据性质进行相关的应用。教学难点：定理证明的思路分析和书写方法。
什么是平行线？ 在同一平面内，不相交的两条直线叫平行线．
同位角、内错角、同旁内角的特点：
解：同位角∠EGB与∠EHD 、 ∠EGA与∠EHC 、 ∠BGF与∠DHF 、 ∠AGF与∠CHF，内错角∠BGF与∠EHC、 ∠AGF与∠EHD ，同旁内角∠AGF与∠CHE 、 ∠BGF与∠EHD
如图，直线AB、CD被直线EF所截，图中哪些角是同位角？哪些角是内错角？哪些角是同旁内角？
小明采用下面的方法作出了平行线，你认为他的作法对吗？为什么？
解：小明的作法对。理由：两条直线被第三条直线所截，如果同位角相等,那么这两条直线平行.
已知：如图，∠1和∠2是直线a，b 被直线 c 截出的内错角，且∠1=∠2.求证：a∥b.
证明：∵ ∠1=∠2 (已知),
∠1=∠3(对顶角相等).
∴∠3=∠2 (等量代换).
∴ a∥b(同位角相等，两直线平行).
定理：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.简单说成:内错角相等，两直线平行.
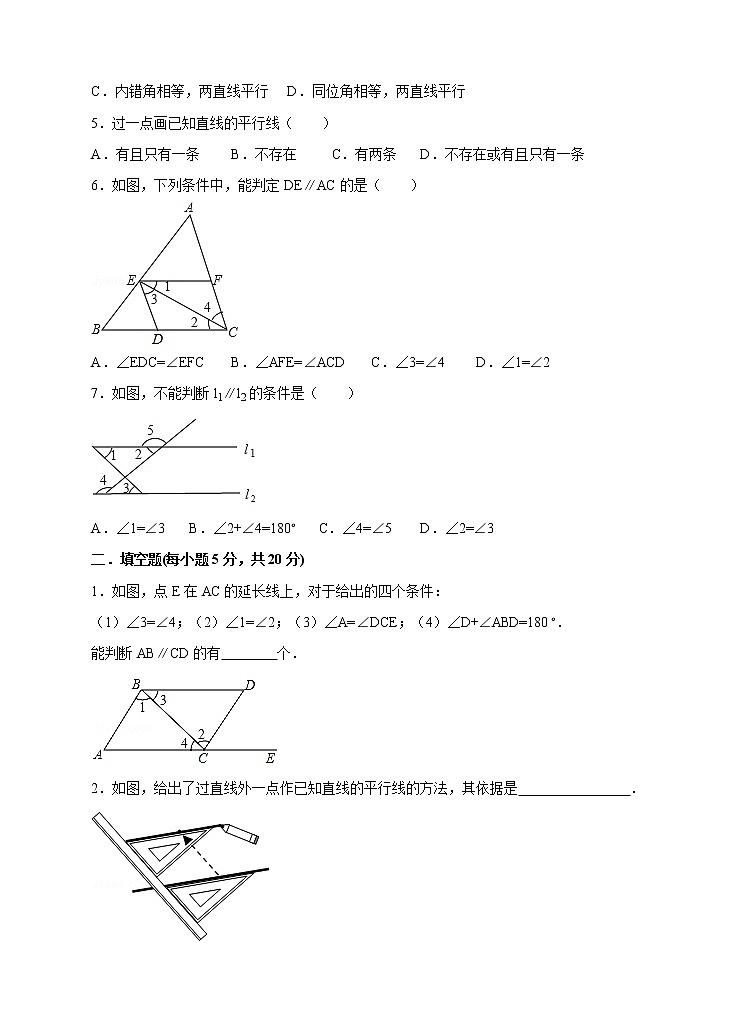
1.如图，由∠1=∠2得到AB∥CD的理由是（　　）A．两直线平行，同位角相等B．两直线平行，内错角相等C．同位角相等，两直线平行D．内错角相等，两直线平行
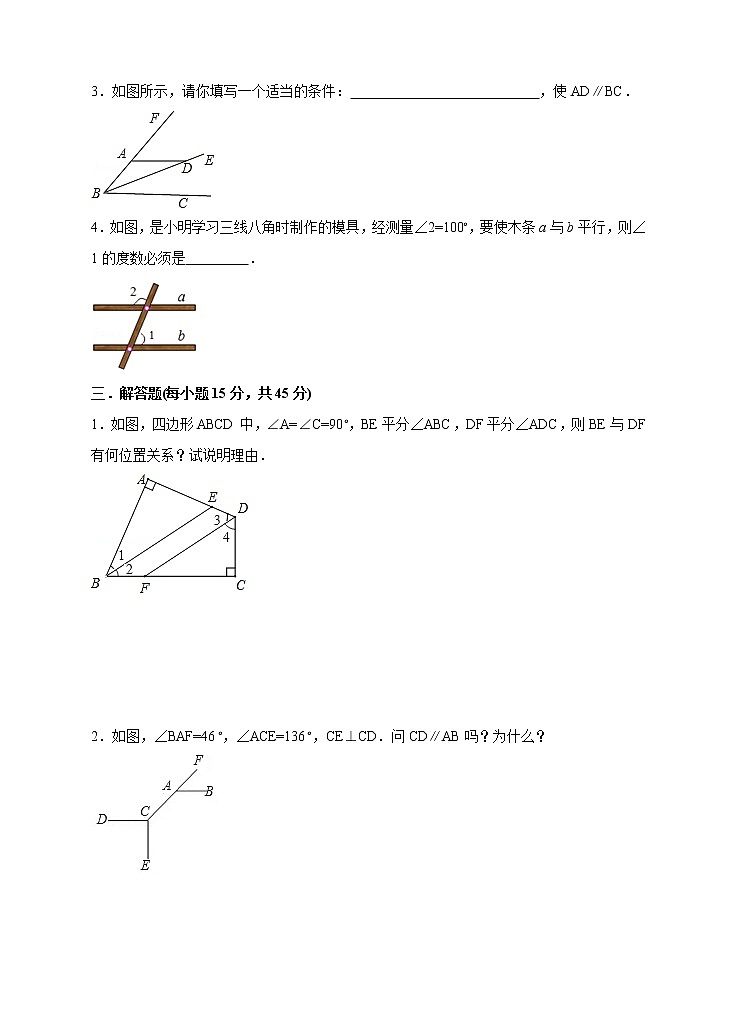
2.如图，已知CD⊥AD，DA⊥AB，∠1＝∠2，则DF与AE平行吗？为什么？
解：DF∥AE.理由如下：∵CD⊥AD，DA⊥AB(已知)∴∠2＋∠FDA＝90°，∠1＋∠DAE＝90°(垂直的定义)．又∵∠1＝∠2(已知)∴∠FDA＝∠DAE(等角的余角相等)∴FD∥AE(内错角相等，两直线平行)
已知：如图，∠1和∠2是直线a，b被直线c截出的同旁内角，且∠1与∠2互补求证：a∥b.
证明:∵ ∠1与∠2互补 (已知)
∴∠1+∠2=1800(互补的定义)
∴∠1= 1800 -∠2(等式的性质)
又∵∠3+∠2=1800 (平角的定义)
∴∠3= 1800 -∠2(等式的性质)
∴∠1=∠3(等量代换)
∴ a∥b(同位角相等，两直线平行)
定理 两条直线被第三条直线所截，如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补，两直线平行.
1.如图，能判定EC∥AB的条件是（　　）A．∠B+∠BCE=1800 ， B．∠A=∠ECDC．∠B=∠BCED．∠A=∠ACB
2.已知，如图直线a，b被直线c所截，且∠1+∠2=1800求证：a∥b.你有几种证明方法
证明：方法1：∵ ∠1+∠2=1800 ，∠1+∠4=1800∴∠2=∠4∴ a∥b(同位角相等，两直线平行).
证明：方法2：∵ ∠1+∠2=1800 ，∠1+∠5=1800∴∠2=∠5∴ a∥b(内错角相等，两直线平行).
证明：方法3：∵ ∠1+∠2=1800 ，∠1=∠3∴ ∠3+∠2=1800 ∴ a∥b(同旁内角互补，两直线平行).
∵AB⊥EF，CD⊥EF（已知）
∴AB∥ CD（同位角相等，两直线平行.)
结论：同垂直于同一直线的两条直线平行.
∴ ∠1=∠2 =90 °（垂直的定义）
 1.在同一平面内，有4条互不重合的直线，L1，L2，L3,L4，若L1⊥L2，L2∥L3，L3⊥L4，则L1和L4的位置关系是（   ） 
解答： 解：∵ L1⊥L2, L2∥L3，∴L3⊥L1 又∵L3⊥L4，∴L1∥L4（同垂直于同一直线的两条直线平行） 故选A
A． 平行 B． 垂直 C． 平行或垂直 D． 无法确定  
 2.如图所示，AC⊥BC，DE⊥BC，CD⊥AB，∠ACD=40°，则∠BDE等于（ ）
解答： 解：∵AC⊥BC，DE⊥BC， ∴DE∥AC， ∴∠EDC=∠ACD=40° 又CD⊥AB， ∴∠BDE=90°﹣∠EDC =90°﹣40°=50°； 故选B
（1）从∠1=∠2，可以推出 ∥ ， 理由是 .（2）从∠2=∠ ，可以推出c∥d ， 理由是 .（3）如果∠1=75°，∠4=105°， 可以推出 ∥ . 理由是 .
内错角相等，两直线平行
同位角相等，两直线平行
同旁内角互补，两直线平行
2．如图，∠1=70°，∠2=110°，AB与ED平行吗？为什么？
证明：AB与ED平行，∵∠1+∠COA=180°，∠1=70°，∴∠COA=180°﹣70°=110°，∵∠2=110°，∴∠AOC=∠2，∴AB∥ED．
1．如图①，将一副直角三角板放在同一条直线AB上，其中∠ONM=30°，∠OCD=45°．（1）将图①中的三角板OMN沿BA的方向平移至图②的位置，MN与CD相交于点E，求∠CEN的度数；（2）将图①中的三角板OMN绕点O按逆时针方向旋转至如图③，当∠CON=5∠DOM时，MN与CD相交于点E，请你判断MN与BC的位置关系，并求∠CEN的度数
解：（1）在△CEN中，∠CEN=180°﹣30°﹣45°=105°； （2）如图②，∵∠CON=5∠DOM∴180°﹣∠DOM=5∠DOM，∴∠DOM=30°∵∠OMN=60°∴MN⊥OD，∴MN∥BC，∴∠CEN=180°﹣∠DCO=180°﹣45°=135°；
教材174页习题第2题