初中数学人教版九年级下册27.2 相似三角形综合与测试教学演示课件ppt

这是一份初中数学人教版九年级下册27.2 相似三角形综合与测试教学演示课件ppt，共19页。PPT课件主要包含了课堂目标，问题导入，模型讲解，模型总结，例题讲解，强化练习，课堂总结等内容，欢迎下载使用。

能够理解并识别出对角互补模型能够掌握对角互补模型的关键特征、证明及结论能够运用对角互补模型并进行相关的证明应用
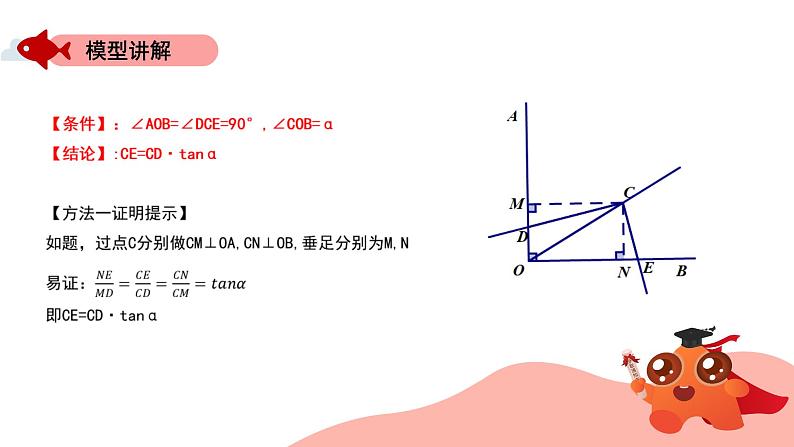
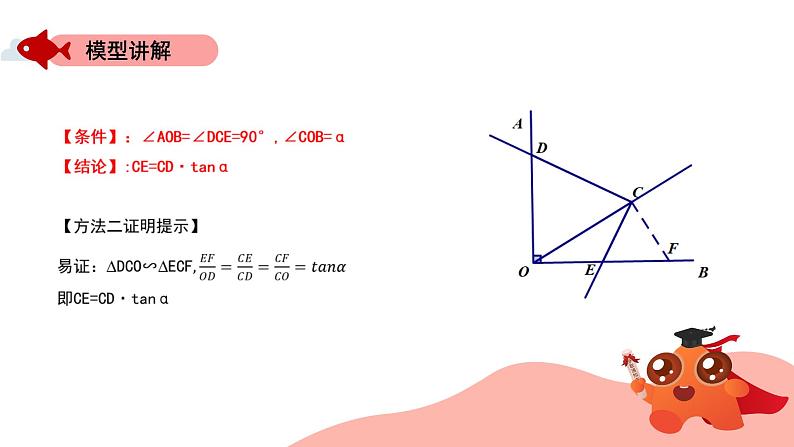
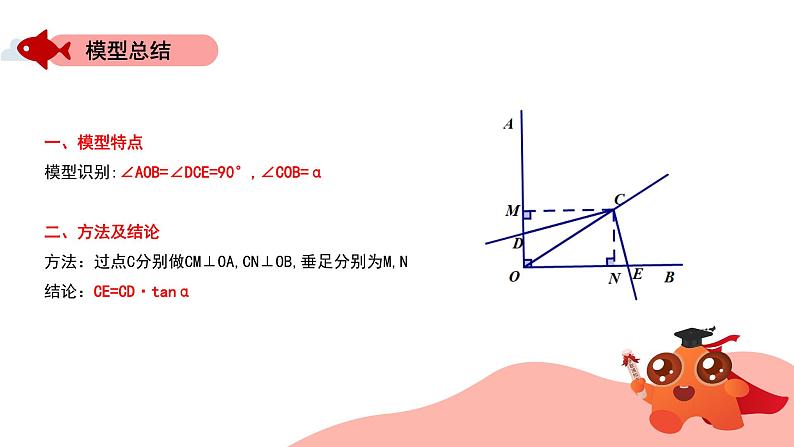
一、模型特点模型识别:∠AOB=∠DCE=90°,∠COB=α二、方法及结论方法：过点C分别做CM⊥OA,CN⊥OB,垂足分别为M,N结论：CE=CD·tanα
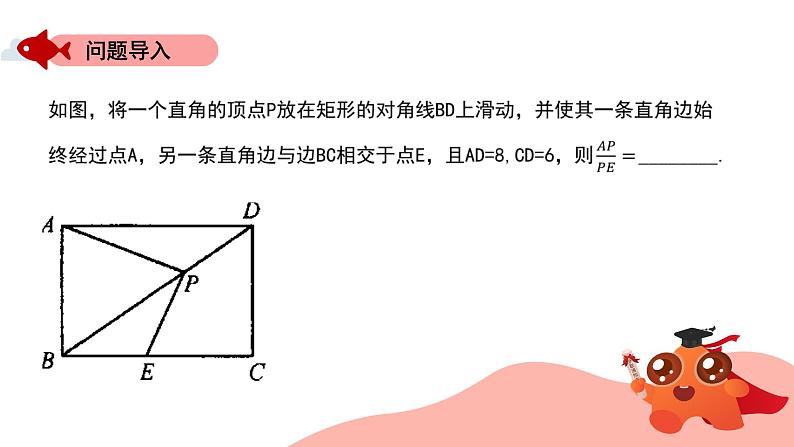
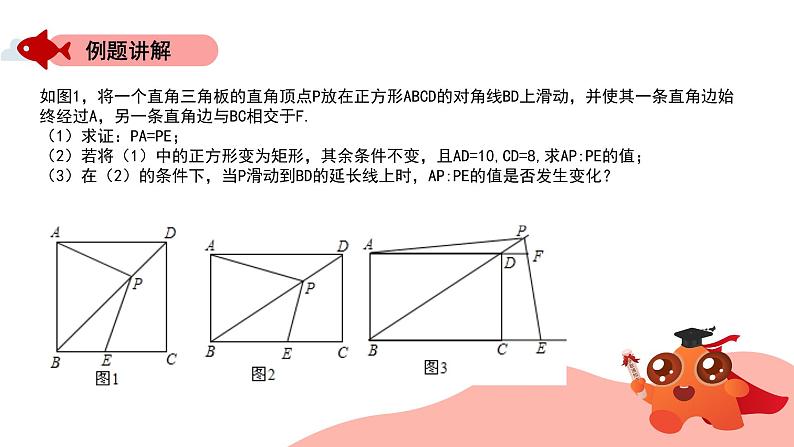
如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过A，另一条直角边与BC相交于F.（1）求证：PA=PE；（2）若将（1）中的正方形变为矩形，其余条件不变，且AD=10,CD=8,求AP:PE的值；（3）在（2）的条件下，当P滑动到BD的延长线上时，AP:PE的值是否发生变化？
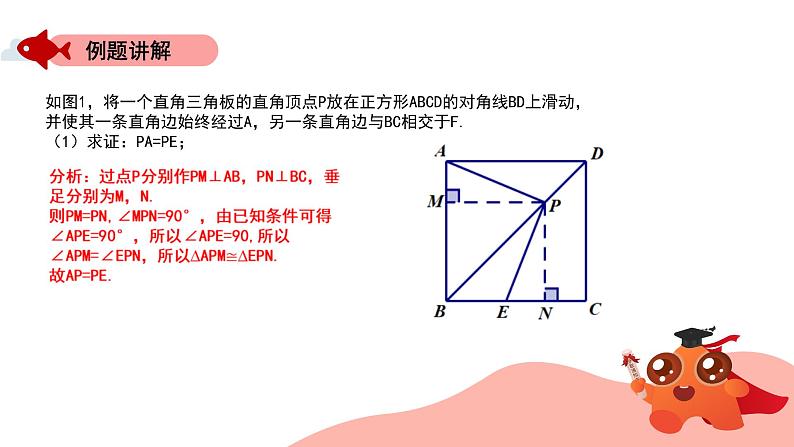
如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过A，另一条直角边与BC相交于F.（1）求证：PA=PE；
如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过A，另一条直角边与BC相交于F.（1）求证：PA=PE；（2）若将（1）中的正方形变为矩形，其余条件不变，且AD=10,CD=8,求AP:PE的值；
分析：AP:PF的值不变，理由同（2）.
∵∠CBD=∠EBF=60°∴∠CBF=∠DBE∴△BCF≌△BDE∴CF=DE∵DE+AE=AD=BC∴CF+AE=BC
证明：作∠ABC的角平分线交AD于点G ∵∠ABC=180°-∠C=120° 又∵BG平分∠ABC ∠CBG=∠ABG=60° ∵∠A=∠C=60° ∴△ABG是等边三角形 ∴ ∠C=∠BGE=60° ∵∠CBG=∠EBF=60°
如图，在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝4，Rt△MPN，∠MPN＝90°，点P在AC上，PM交AB于点E，PN交BC于点F，当PE＝2PF时，AP为多长？
如图，在矩形ABCD中，AB＝3，BC＝5，点E在对角线AC上，连接BE，作EF⊥BE，垂足为E，直线EF交线段DC于点F，则EF：BE＝（ ）
如图，四边形ABCD被对角线BD分为等腰Rt△ABD和Rt△CBD，其中∠BAD和∠BCD都是直角，另一条对角线AC的长度为2，则四边形ABCD的面积为_________．
在数学活动中，我们已经学习了四点共圆的条件：如果一个四边形对角互补，那么这个四边形的四个顶点在同一个圆上，简称“四点共圆”．如图，已知四边形ABCD，AD=4，CD=3，AC=5，cs∠BCA=sin∠BAC=1/2，求∠BDC的大小．
三、考法：（1）证线段相等（2）求线段比值