冀教版九年级上册26.4 解直角三角形的应用教学演示ppt课件

这是一份冀教版九年级上册26.4 解直角三角形的应用教学演示ppt课件，共24页。PPT课件主要包含了3边角之间的关系，解直角三角形的原则，解由题意得，简单实际问题，数学模型，数学建模及方程思想，解题方法小结等内容，欢迎下载使用。
一般地，直角三角形中，除直角外，共有5个元素，即3条边和2个锐角，由直角三角形中除直角外的已知元素，求出其余元素的过程，叫做解直角三角形。
探究：（1）在直角三角形中，除直角外的5个元素之间有哪些关系？ （2）知道5个元素中的几个，就可以求出其余元素？
（1）两锐角这间的关系 ∠A＋ ∠ B＝90°
（2）两边之间的关系：a2+b2=c2
如图：在Rt△ABC中，除直角C外的5个元素之间有如下关系：
利用上面的关系，知道其中的2个元素（至少有一个是边），就可以求出其余的3个未知元素。
（1）有角先求角，无角先求边
（2）有斜用弦, 无斜用切；
宁乘毋除, 取原避中。
例1：在Rt▲ABC中，∠C=900，AC= ，BC= ，解这个直角三角形。
例2：在Rt▲ABC中， ∠C=900， ∠ B=350，b=20，解这个直角三角形。（结果保留小数点后一位）
在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上向下看，视线与水平线的夹角叫做俯角
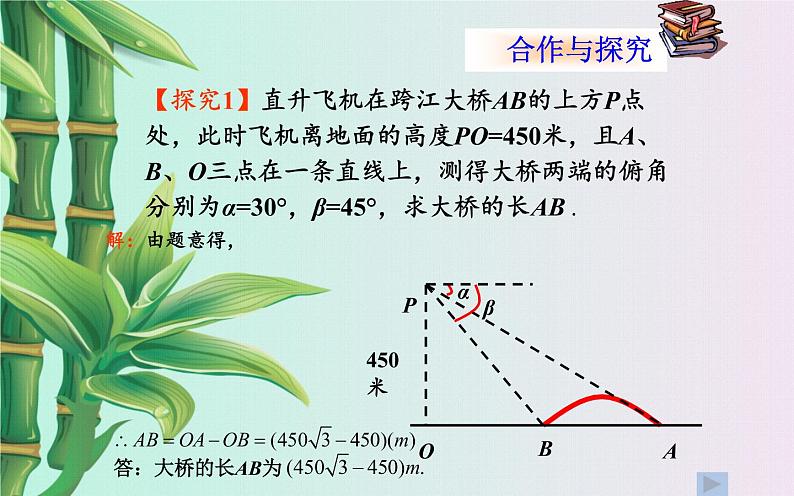
【探究1】直升飞机在跨江大桥AB的上方P点处，此时飞机离地面的高度PO=450米，且A、B、O三点在一条直线上，测得大桥两端的俯角分别为α=30°，β=45°，求大桥的长AB .
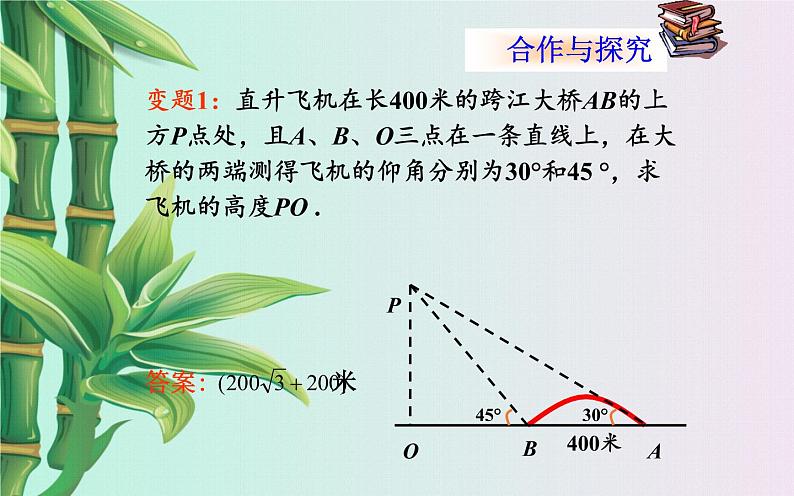
变题1：直升飞机在长400米的跨江大桥AB的上方P点处，且A、B、O三点在一条直线上，在大桥的两端测得飞机的仰角分别为30°和45 °，求飞机的高度PO .
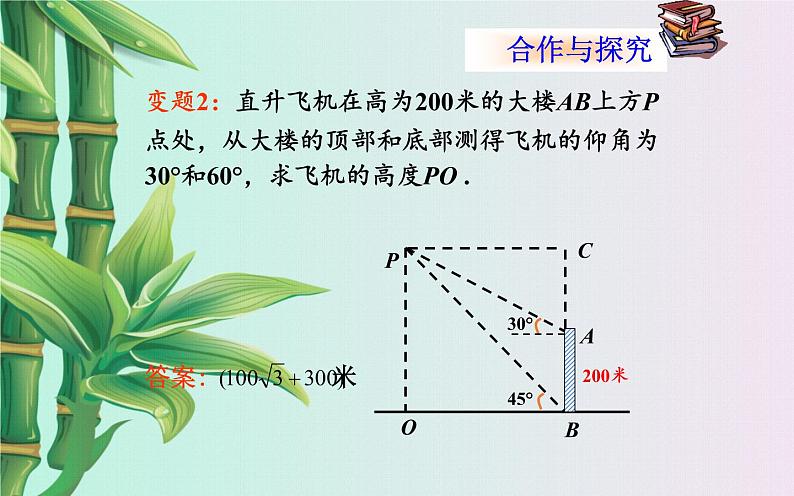
变题2：直升飞机在高为200米的大楼AB上方P点处，从大楼的顶部和底部测得飞机的仰角为30°和60°，求飞机的高度PO .
变题3：直升飞机在高为200米的大楼AB左侧P点处，测得大楼的顶部仰角为45°,测得大楼底部俯角为30°，求飞机与大楼之间的水平距离.
答案：AB≈520（米）
变题4：（2008桂林）汶川地震后，抢险队派一架直升飞机去A、B两个村庄抢险，飞机在距地面450米上空的P点，测得A村的俯角为30°，B村的俯角为60°（如图5）．求A、B两个村庄间的距离．（结果精确到米，参考数据 ）.
练习：1、2003年10月15日“神舟”5号载人航天飞船发射成功。当飞船完成变轨后，就在离地球表面350km的圆形轨道上运行，如图，当飞船运行到地球表面上P点的正上方时，从飞船上能直接看到地球上最远的点在什么位置？这样的最远点与P点的距离是多少？（地球半径约为6400km，Π取3.142，结果保留整数）
2、热气球的探测器显示，从热气球看一栋高楼顶部的仰角为300，看这栋楼底部的俯角为600，热气球与离楼的水平距离为120m，这栋高楼有我高？（结果保留小数后一位） 3、如图，一艘海轮位于灯塔P的北偏东650方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到过位于灯塔P的南偏东340方向上的B处，这时，海轮所在的B处距离灯塔P有多远？（结果保留小数点后一位）
【探究2】学生小王帮在测绘局工作的爸爸买了一些仪器后与同学在环西文化广场休息，看到濠河对岸的电视塔，他想用手中的测角仪和卷尺不过河测出电视塔空中塔楼的高度.现已测出∠ADB=40°，由于不能过河，因此无法知道BD的长度，于是他向前走50米到达C处测得∠ACB=55°，但他们在计算中碰到了困难，请大家一起想想办法，求出电视塔塔楼AB的高.
答案：空中塔楼AB高约为105米
【探究3】 在我市迎接奥运圣火的活动中，某校教学楼上悬挂着宣传条幅DC，小丽同学在点A处，测得条幅顶端D的仰角为30°，再向条幅方向前进10米后， 又在点B处测得条幅顶端D的仰角为45°，已知点A、B和C离地面高度都为1.44米，求条幅顶端D点距离地面的高度．（计算结果精确到0.1米） 参考数据:
通过作高转化为直角三角形
1．把实际问题转化成数学问题，这个转化包括两个方面：一是将实际问题的图形转化为几何图形，画出正确的示意图；二是将已知条件转化为示意图中的边、角或它们之间的关系.
2．把数学问题转化成解直角三角形问题，如果示意图不是直角三角形，可添加适当的辅助线，画出直角三角形.
2.如图2，在离铁塔BE 120m的A处，用测角仪测量塔顶的仰角为30°，已知测角仪高AD=1.5m，则塔高BE= _________ （根号保留）．
1.如图1，已知楼房AB高为50m，铁塔塔基距楼房地基间的水平距离BD为100m，塔高CD为 m，则下面结论中正确的是（ ）A．由楼顶望塔顶仰角为60°B．由楼顶望塔基俯角为60°C．由楼顶望塔顶仰角为30° D．由楼顶望塔基俯角为30°
3.如图3，从地面上的C，D两点测得树顶A仰角分别是45°和30°，已知CD=200m，点C在BD上，则树高AB等于 （根号保留）．
4.如图4，将宽为1cm的纸条沿BC折叠，使∠CAB=45°，则折叠后重叠部分的面积为 （根号保留）．
思考1：一架直升机从某塔顶Ａ测得地面C、D两点的俯角分别为30°、 45°，若C、D与塔底Ｂ共线，CD＝200米，求塔高AB？
思考2：有一块三形场地ABC，测得其中AB边长为60米，AC边长50米，∠ABC=30°，试求出这个三角形场地的面积．
必做题：书本P93/4、P94/7题．
课后思考：如图，某幼儿园为了加强安全管理，决定将园内的滑滑板的倾角由45º降为30º，已知原滑滑板AB的长为5米，点D、B、C 在同一水平地面上．（1）改善后滑滑板会加长多少？（精确到0．01）（2）若滑滑板的正前方能有3米长的空地就能保证安全，原滑滑板的前方有6米长的空地，像这样改造是否可行？说明理由 (参考数据： ）