初中数学苏科版八年级下册第9章 中心对称图形——平行四边形9.2 中心对称与中心对称图形教学课件ppt

这是一份初中数学苏科版八年级下册第9章 中心对称图形——平行四边形9.2 中心对称与中心对称图形教学课件ppt，共20页。PPT课件主要包含了中心对称的性质，旋转90°，旋转180°，旋转270°，旋转360°，旋转n×90°，课后回顾等内容，欢迎下载使用。
1、中心对称的两个图形，对称点所连线段经过对称中心，而且被对称中心所平分。2、中心对称的两个图形是全等形。
学习目标1.理解中心对称图形的概念。2.准确判断某图形是否是中心对称图形。重点中心对称图形的定义及了解一些简单图形的对称性。难点中心对称图形和中心对称的关系。
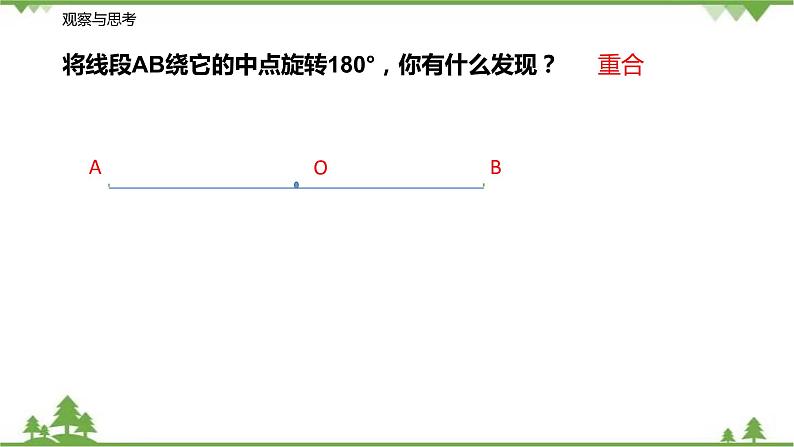
将线段AB绕它的中点旋转180°，你有什么发现？
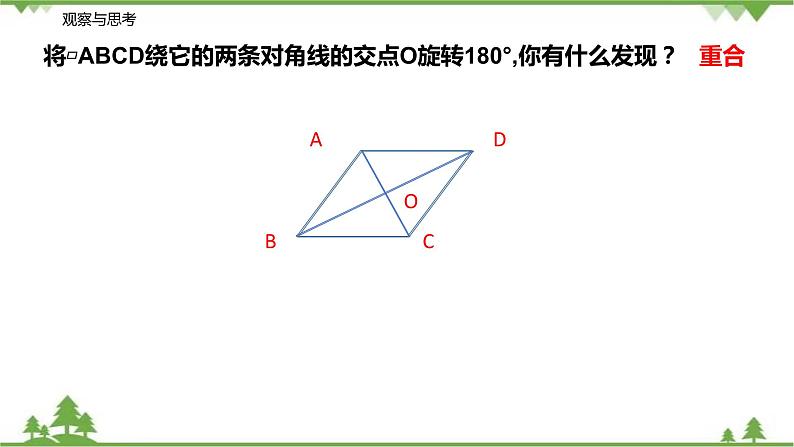
将▱ABCD绕它的两条对角线的交点O旋转180°,你有什么发现？
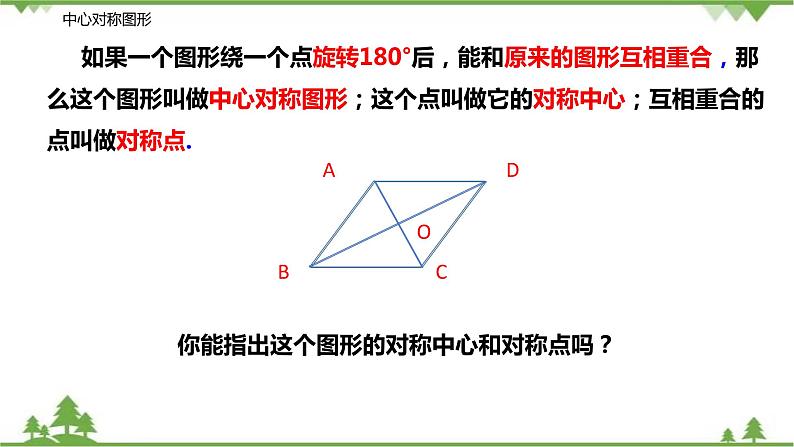
如果一个图形绕一个点旋转180°后，能和原来的图形互相重合，那么这个图形叫做中心对称图形；这个点叫做它的对称中心；互相重合的点叫做对称点.
你能指出这个图形的对称中心和对称点吗？
探索中心对称图形的性质
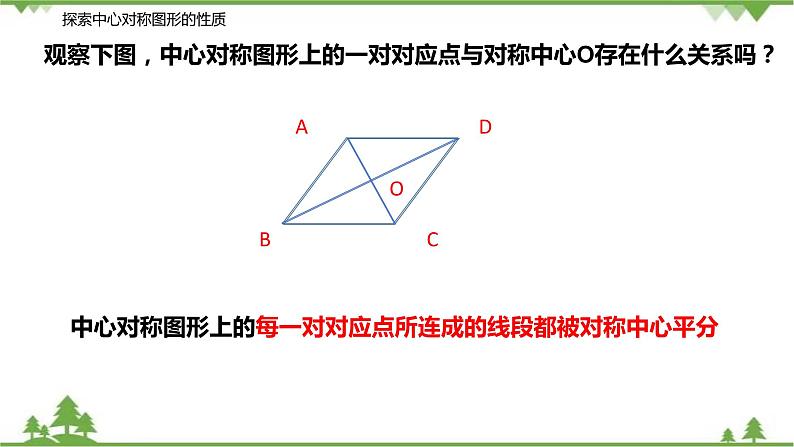
观察下图，中心对称图形上的一对对应点与对称中心O存在什么关系吗？
中心对称图形上的每一对对应点所连成的线段都被对称中心平分
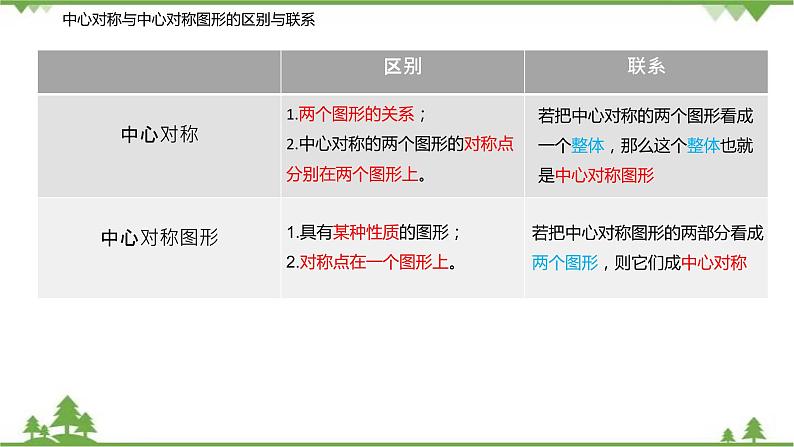
中心对称与中心对称图形的区别与联系
1.两个图形的关系；2.中心对称的两个图形的对称点分别在两个图形上。
1.具有某种性质的图形；2.对称点在一个图形上。
若把中心对称的两个图形看成一个整体，那么这个整体也就是中心对称图形
若把中心对称图形的两部分看成两个图形，则它们成中心对称
生活中常见的中心对称图形
正方形是中心对称图形吗？正方形绕两条对角线的交点旋转多少度能与原来的图形重合？能由此验证正方形的一些特殊性质吗？
【结论】正方形绕两条对角线的交点旋转900或其整数倍，都能与原来的图形重合。因此，可以验证正方形的四边相等、四角相等、对角线互相垂直平分等性质。
正三角形是中心对称图形吗？正方形呢？正五边形呢？正六边呢？你能发现什么规律？
边数为偶数的正多边形都是中心对称图形。
A B C E S O W N I x Y Z
下列这些字母中有_____个是中心对称的图形。有____个是轴对称的图形。
下列这些数字中有_____个是中心对称的图形。有_____个是轴对称的图形。
观察右侧车标，请指出哪些是轴对称图形，哪些是中心对称图形？
1．图1和图2中所有的小正方形都全等，将图1的正方形放在图2中①、②、③、④的某个位置，使它与原来7个小正方形组成的图形是中心对称图形.这个位置是（ ）A．①B．②C．③D．④
2．下列各类标志中，既是轴对称图形，又是中心对称图形的是（ ）A．4个B．3个C．2个D．1个
【答案】C【详解】解：第一个是轴对称图形，也是中心对称图形；第二个是轴对称图形，不是中心对称图形；第三个是轴对称图形，也是中心对称图形；第四个是轴对称图形，不是中心对称图形；故符合题意的图形有2个，故选：C．
3．如图，它是一个中心对称图形，则此图形的对称中心为（　　）A．A点 B．B点 C．C点 D．D点
【答案】B【详解】解：如图所示：点A与点C是对应点，点D与点E是对应点，线段AC与DE相交于点B，所以点B是对称中心．故选B．
4．在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是（ ）A．①B．②C．③D．④
中心对称和中心对称图形的区别和联系
判断图形是否中心对称图形