初中数学冀教版八年级上册17.5 反证法示范课课件ppt

这是一份初中数学冀教版八年级上册17.5 反证法示范课课件ppt，共16页。PPT课件主要包含了问题思考，活动一反证法，活动二应用举例等内容，欢迎下载使用。

三个古希腊哲学家甲、乙、丙,由于争论和天气炎热感到疲倦了,于是在花园里的一棵大树下躺下来休息一会儿,结果都睡着了.这时一个爱开玩笑的人用炭涂黑了他们的前额.三个人醒来以后,彼此看了看,都笑了起来.但这并没有引起他们之中任何一个人的担心,因为每个人都以为是其他两人在互相取笑.其中甲突然不笑了,因为他发觉自己的前额也被涂黑了.他是怎样觉察到的呢?你能想出来吗?
4.根据原来的假设:前额没被涂黑是错误的,便可知道没被涂黑的反面——被涂黑了是正确的结论.简单地说,甲是通过说明前额被涂黑了的反面——没被涂黑是错误的,从而觉察到自己的前额被涂黑了.
仔细分析甲的思考过程,不难看出它分4个步骤:
1.假设自己的前额没被涂黑;
2.根据这个假设进行推理,推得一个与乙对丙的笑不感到奇怪的这个事实相矛盾的结果——乙应对丙的笑感到奇怪;
3.根据这个矛盾,说明原来假设自己的前额没被涂黑是错误的;
已知:如图所示, △ABC. 求证:在△ABC中,如果它含直角,那么它只能有一个直角.
这与“三角形的内角和等于180°”相矛盾,因此三角形有两个(或三个)直角的假设是不成立的.所以如果三角形含直角,那么它只能有一个直角.
证明:假设△ABC中有两个(或三个)直角，不妨设∠A=∠B=90°，∵∠A+∠B=180°，∴∠A+∠B+∠C=180°+∠C>180°，
总结：反证法是间接证明的方法
第三步:由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的.
用反证法证明一个命题是真命题的一般步骤.
第一步:假设命题的结论不成立.
第二步:从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实、已证明的定理、性质或题设条件相矛盾的结果.
用反证法证明平行线的性质定理一:两条平行线被第三条直线所截,同位角相等.
已知:如图所示，直线AB∥CD，直线EF分别与直线AB,CD交于点G，H，∠1和∠2是同位角. 求证:∠1=∠2.
证明:假设∠1≠∠2.过点G作直线MN，使得∠EGN=∠1.∵∠EGN=∠1，∴MN∥CD(基本事实).
又∵AB∥CD(已知)，∴过点G，有两条不同的直线AB和MN都与直线CD平行.这与“经过已知直线外一点,有且只有一条直线和已知直线平行”相矛盾.∴∠1≠∠2的假设是不成立的.因此∠1=∠2.
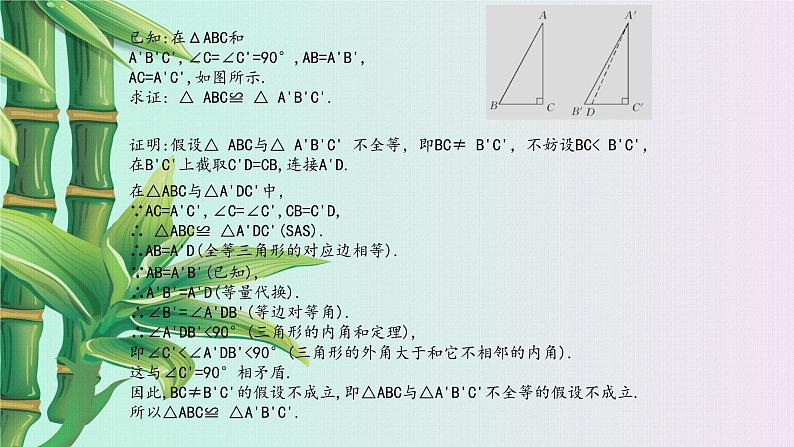
已知:在ΔABC和A'B'C',∠C=∠C'=90°,AB=A'B',AC=A'C',如图所示. 求证: △ ABC≌ △ A'B'C'.
证明:假设△ ABC与△ A'B'C' 不全等，即BC≠ B'C'，不妨设BC< B'C'，在B'C'上截取C'D=CB,连接A'D.
在△ABC与△A'DC'中，∵AC=A'C',∠C=∠C',CB=C'D,∴ △ABC≌ △A'DC'(SAS).∴AB=A'D(全等三角形的对应边相等).
∵AB=A'B'(已知),∴A'B'=A'D(等量代换).∴∠B'=∠A'DB'(等边对等角).∴∠A'DB'<90°(三角形的内角和定理),
即∠C'<∠A'DB'<90°(三角形的外角大于和它不相邻的内角).这与∠C'=90°相矛盾.因此,BC≠B'C'的假设不成立,即△ABC与△A'B'C'不全等的假设不成立.所以△ABC≌ △A'B'C'.
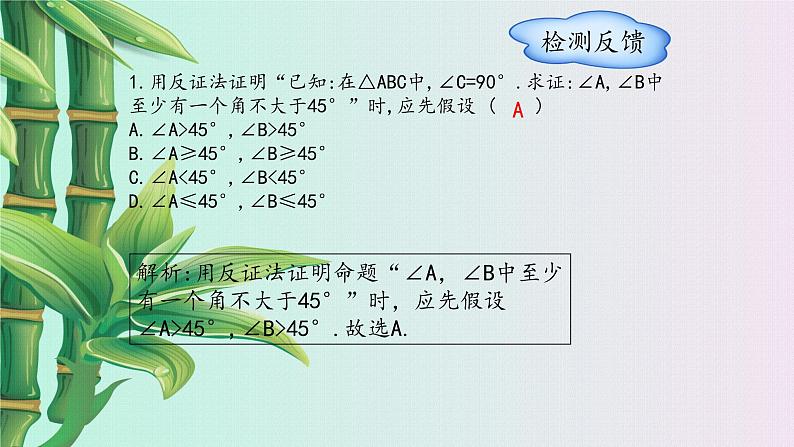
1.用反证法证明“已知:在△ABC中,∠C=90°.求证:∠A,∠B中至少有一个角不大于45°”时,应先假设(　　)A.∠A>45°,∠B>45°B.∠A≥45°,∠B≥45°C.∠A<45°,∠B<45°D.∠A≤45°,∠B≤45°
解析:用反证法证明命题“∠A，∠B中至少有一个角不大于45°”时，应先假设∠A>45°,∠B>45°.故选A.
解析:∵当a=1,b=-2或a=0,b=-1或a=-1，b=-2时，a>b，a2b,则a2>b2”是假命题，故A，B，C不符合题意，只有当a=2，b=-1时，“若a>b,则a2>b2”是真命题,故此时a,b的值不能作为反例.故选D.
2.要证明命题“若a>b，则a2>b2”是假命题,下列a，b的值不能作为反例的是(　　)A.a=1，b=-2B.a=0，b=-1C.a=-1，b=-2D.a=2，b=-1
解析:∵“至少有两个”的反面为“至多有一个”,而反证法的假设即原命题的结论不成立,∴应假设:三角形三个外角中至多有一个钝角,也可以假设:三个外角中只有一个钝角.故选D.
3.用反证法证明“三角形的三个外角中至少有两个钝角”时,假设正确的是(　　)A.假设三个外角都是锐角B.假设至少有一个钝角C.假设三个外角都是钝角D.假设三个外角中只有一个钝角
4.用反证法证明“如图所示,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一步是(　　) A.假设AB不平行于CDB.假设AB不平行于EFC.假设CD∥EFD.假设CD不平行于EF
解析:∵用反证法证明命题“如果AB∥CD,AB∥EF,那么CD∥EF,”∴证明的第一步应是:从结论反面出发,假设CD不平行于EF.故选D.
5.用反证法证明三角形的一个外角等于与它不相邻的两个内角的和.
解析:首先假设三角形的一个外角不等于与它不相邻的两个内角的和,根据三角形的内角和等于180°,得到矛盾,所以假设不成立,进而可知三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图所示,∠1是ΔABC的一个外角. 求证:∠1=∠A+∠B.
证明:假设∠1≠∠A+∠B,在ΔABC中,∠A+∠B+∠2=180°,∵∠1+∠2=180°, ∴∠2=180°-∠1,∵∠1≠∠A+∠B,∴∠2≠180°-(∠A+∠B)∴∠A+∠B+∠2≠180°.与“三角形的内角和等于180°”相矛盾,∴假设不成立,原命题成立,即∠1=∠A+∠B.
6.用反证法证明一个三角形中不可能有两个角是钝角.
解析:根据反证法的证明方法先假设,进而证明即可.
已知:ΔABC.求证:∠A,∠B,∠C中不可能有两个角是钝角.
证明:假设∠A,∠B,∠C中有两个角是钝角,不妨设∠A,∠B为钝角,∴∠A+∠B>180°,这与三角形内角和定理相矛盾,故假设不成立,原命题正确.即一个三角形中不可能有两个角是钝角.
7.请用反证法证明“如果两个整数的积是偶数,那么这两个整数中至少有一个是偶数.”
解析:首先假设这两个整数都是奇数,其中一个奇数为2n+1,另一个奇数为2p+1,利用多项式乘以多项式得出(2n+1)(2p+1)=2(2np+n+p)+1,进而得出矛盾,则原命题正确.
证明:假设这两个整数都是奇数,其中一个奇数为2n+1,另一个奇数为2p+1(n,p为整数),则(2n+1)(2p+1)=2(2np+n+p)+1,∵无论n,p取何值,2(2np+n+p)+1都是奇数,这与两个整数的积为偶数相矛盾,∴假设不成立,∴这两个整数中至少有一个是偶数.
解:(1)取a=2,b=-1,则a+b=1>0,但ab=-2<0.所以此命题是假命题.(2)取a=1+ ,b=1- ,a,b均为无理数,但a+b=2是有理数.所以此命题是假命题.(3)如图所示,在ΔABC与ΔABD中,AB=AB,AD=AC,∠ABD=∠ABC,但ΔABC与ΔABD显然不全等.所以此命题是假命题.
8.试用举反例的方法说明下列命题是假命题.
举例:如果ab<0,那么a+b<0.反例:设a=4,b=-3,则ab=4×(-3)=-12<0,但a+b=4+(-3)=1>0,所以这个命题是假命题.
(1)如果a+b>0,那么ab>0;(2)如果a是无理数,b是无理数,那么a+b是无理数;(3)两个三角形中,两边及其中一边的对角对应相等,则这两个三角形全等(画出图形,并加以说明).
解析:(1)此题是一道开放题,可举的反例很多,但只举一例即可.如果a+b>0,那么ab>0,所举的反例是a,b一个为正数,一个为负数,且正数的绝对值大于负数.(2)可利用平方差公式找这样的无理数,比如1± ,两数相加就是有理数.(3)此题主要利用三角形全等的判定方法来举例,在这里注意,没有边边角定理.