2021学年第22章 相似形22.3 相似三角形的性质第1课时课后测评

这是一份2021学年第22章 相似形22.3 相似三角形的性质第1课时课后测评，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.已知△ABC∽△DEF,若△ABC与△DEF的相似比为34,则△ABC与△DEF对应中线的比为( )
A.34B.43C.916D.169
2.已知△ABC∽△DEF,且相似比为1∶2,则△ABC与△DEF的面积比为( )
A.1∶4B.4∶1C.1∶2D.2∶1
3.[2020·铜仁] 已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3B.2C.4D.5
4.如果两个相似三角形的面积比为1∶4,那么它们的周长比是( )
A.1∶16B.1∶4C.1∶6D.1∶2
5.如图1,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为16,阴影部分三角形的面积为9.如果AA'=1,那么A'D的长为( )
图1
A.2B.3C.4D.32
6.如图2,在△ABC中,点D,F在AB边上,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形FBCG,则AD∶DF∶FB的值为( )
图2
A.1∶1∶1B.1∶2∶3
C.1∶2∶3D.1∶(2-1)∶(3-2)
7.如图3,D,E分别是△ABC的边AB,BC上的点,DE∥AC.若S△BDE∶S△CDE=1∶3,则S△DOE∶S△COA的值为( )
图3
A.13B.14C.19D.116
二、填空题
8.已知△ABC∽△A'B'C',ABA'B'=12,△ABC的角平分线CD=4 cm,△ABC的面积为64 cm2.△A'B'C'的角平分线C'D'的长为 ,△A'B'C'的面积为 .
9.在△ABC中,D,E分别是边AB,AC的中点,则△ADE与△ABC的周长之比为 .
10.如图4,在▱ABCD中,AE∶EB=3∶4,DE交AC于点F,则△AEF与△CDF的周长之比为 ;若△CDF的面积为14 cm2,则△AEF的面积为 .
图4
11.如图5,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=6 m,点P到CD的距离是2.7 m,则AB离地面的距离为 m.
图5
12.[2020·东营] 如图6,P为平行四边形ABCD的边BC上一点,E,F分别为PA,PD上的点,且PA=3PE,PD=3PF,△PEF,△PDC,△PAB的面积分别记为S,S1,S2,若S=2,则S1+S2= .
图6
三、解答题
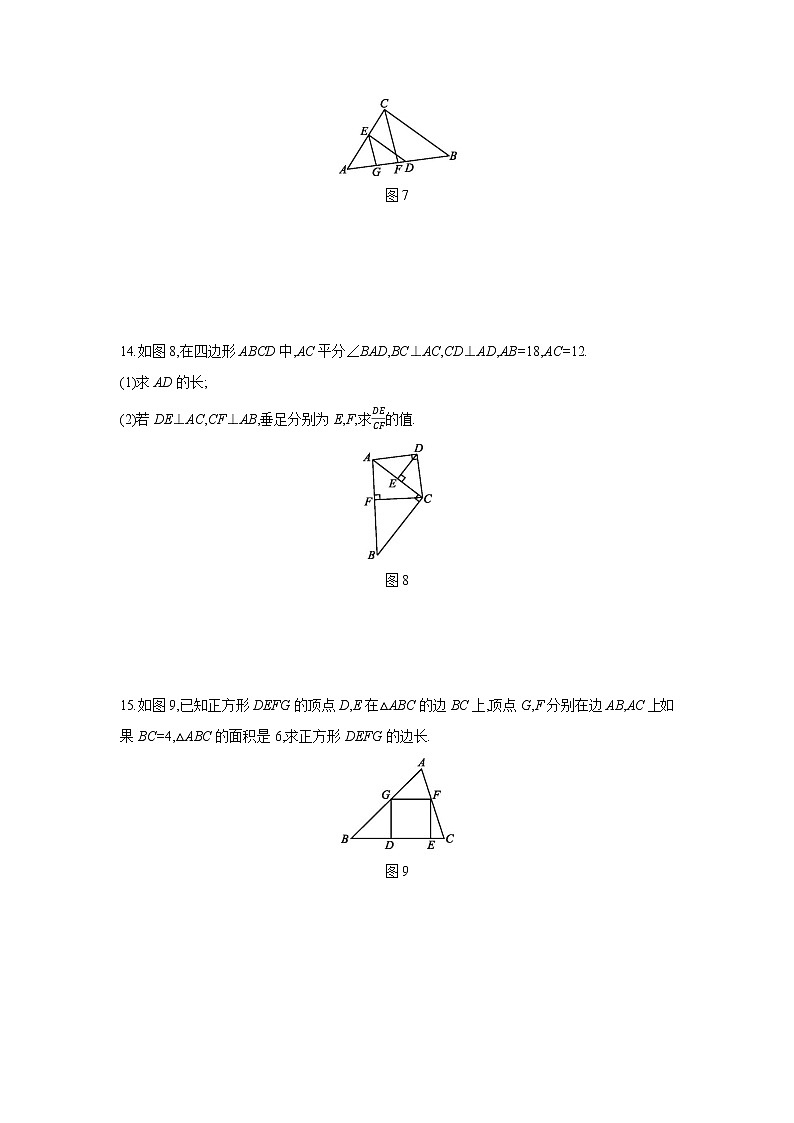
13.如图7,在△ABC中,D,E分别是△ABC的AB,AC边上的点,DE∥BC,CF,EG分别是△ABC与△ADE的中线,已知AD∶DB=4∶3,EG=4 cm,求CF的长.
图7
14.如图8,在四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.
(1)求AD的长;
(2)若DE⊥AC,CF⊥AB,垂足分别为E,F,求DECF的值.
图8
15.如图9,已知正方形DEFG的顶点D,E在△ABC的边BC上,顶点G,F分别在边AB,AC上.如果BC=4,△ABC的面积是6,求正方形DEFG的边长.
图9
16.如图10所示,在四边形ABCD中,AD∥BC,CE是∠BCD的平分线,且CE⊥AB,E为垂足,BE=2AE.若四边形AECD的面积为1,求四边形ABCD的面积.
图10
答案
1.A 2.A
3.[解析] A 相似三角形的周长之比等于相似比,所以△FHB和△EAD的相似比为30∶15=2∶1,所以FH∶EA=2∶1,即6∶EA=2∶1,解得EA=3.故选A.
4.[解析] D 如果两个相似三角形的面积比为1∶4,那么这两个相似三角形的相似比为1∶2,∴这两个相似三角形的周长比为1∶2.
5.[解析] B 如图,
∵S△ABC=16,S△A'EF=9,且AD为BC边上的中线,
∴S△A'DE=12S△A'EF=4.5,S△ABD=12S△ABC=8.
∵将△ABC沿BC边上的中线AD平移得到△A'B'C',
∴A'E∥AB,
∴△DA'E∽△DAB,
则(A'DAD)2=S△A'DES△ADB,即(A'DA'D+1)2=4.58,
解得A'D=3或A'D=-37(舍去).
故选B.
6.[解析] D ∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC.
∵S△ADE=S四边形DFGE=S四边形FBCG,
∴S△ADE∶S△AFG∶S△ABC=1∶2∶3,
∴AD∶AF∶AB=1∶2∶3,
∴AD∶DF∶FB=1∶(2-1)∶(3-2).
故选D.
7.[解析] D ∵S△BDE∶S△CDE=1∶3,∴BE∶CE=1∶3.∵DE∥AC,∴△DOE∽△COA,且△BDE∽△BAC,∴DEAC=BEBC=11+3=14,∴S△DOES△COA=DEAC2=142=116.
8.[答案] 8 cm 256 cm2
[解析] ∵△ABC∽△A'B'C',ABA'B'=12,
∴CDC'D'=ABA'B'=12.
∵△ABC的角平分线CD=4 cm,
∴C'D'=4×2=8(cm).
∵△ABC的面积△A'B'C'的面积=(ABA'B')2=14,△ABC的面积为64 cm2,
∴△A'B'C'的面积为64×4=256(cm2).
9.[答案] 12
[解析] 由D,E分别是边AB,AC的中点,得出DE是△ABC的中位线,根据三角形中位线的性质知DE∥BC,进而得到△ADE与△ABC相似,根据相似三角形的性质,得到△ADE与△ABC的周长之比为12.
10.[答案] 3∶7 187 cm2
[解析] ∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∴△AEF∽△CDF.
∵AE∶EB=3∶4,
∴AE∶AB=3∶7,
∴AE∶DC=3∶7.
∵△AEF∽△CDF,
∴△AEF的周长∶△CDF的周长=AE∶DC=3∶7.
∵△AEF∽△CDF,
∴S△CDF∶S△AEF=(CD∶AE)2.
∵CD∶AE=7∶3,△CDF的面积为14 cm2,
∴△AEF的面积为187 cm2.
11.[答案] 1.8
[解析] ∵AB∥CD,∴△PAB∽△PCD.
∵AB=2 m,CD=6 m,∴ABCD=13.
设AB离地面的距离为x m,
∵点P到CD的距离是2.7 m,
∴点P到AB的距离是(2.7-x)m,
∴2.7-x2.7=13,
解得x=1.8.故AB离地面的距离为1.8 m.
12.[答案] 18
[解析] 本题考查了相似三角形的判定、性质,三角形的面积,解题的关键是根据已知条件推出相似三角形,并由相似比得到面积比.
∵PA=3PE,PD=3PF,∠APD=∠EPF,
∴△PEF∽△PAD,相似比为1∶3.
∵△PEF的面积为S=2,
∴S△PAD=9S=9×2=18,
∴S1+S2=S△PAD=18.
13.解:∵AD∶DB=4∶3,
∴AD∶AB=4∶7.
∵DE∥BC,∴△ABC∽△ADE.
∵CF,EG分别是△ABC与△ADE的中线,
∴ADAB=EGCF,
∴47=4CF,
∴CF=7(cm).
14.解:(1)∵AC平分∠BAD,BC⊥AC,CD⊥AD,
∴∠BAC=∠CAD,∠BCA=∠CDA,
∴△ABC∽△ACD,
∴ABAC=ACAD,∴AD=AC2AB=12218=8,
即AD的长为8.
(2)∵△ABC∽△ACD,DE⊥AC,CF⊥AB,
∴DECF=ACAB=23.
15.解:如图,过点A作AH⊥BC于点H,交GF于点M.
∵△ABC的面积是6,
∴12BC·AH=6,
∴AH=2×64=3.
设正方形DEFG的边长为x,
则GF=x,MH=x,
∴AM=3-x.
∵GF∥BC,AH⊥BC,
∴AM⊥GF,△AGF∽△ABC,
∴GFBC=AMAH,即x4=3-x3,解得x=127,
即正方形DEFG的边长为127.
16.解:如图,延长BA与CD,交于点F.
∵AD∥BC,
∴△FAD∽△FBC.
∵CE是∠BCD的平分线,
∴∠BCE=∠FCE.
∵CE⊥AB,
∴∠BEC=∠FEC=90°.
又∵EC=EC,
∴△BCE≌△FCE(ASA),
∴BE=EF,
∴BF=2BE.
∵BE=2AE,
∴EF=2AE,
∴AE=AF,
∴BF=4AE=4AF,
∴S△FADS△FBC=(AFBF)2=116.
设S△FAD=x,
则S△FBC=16x,
∴S△BCE=S△FEC=8x,
∴S四边形AECD=7x.
∵四边形AECD的面积为1,
∴7x=1,
∴x=17,
∴四边形ABCD的面积=S△BCE+S四边形AECD=15x=157.