华师大版九年级上册23.4 中位线备课课件ppt

这是一份华师大版九年级上册23.4 中位线备课课件ppt，共33页。PPT课件主要包含了做一做，DE是三角形ABC的，中位线，三角形的中位线，友情提醒，观察猜想，能说出理由吗，说一说，三角形的中位线的性质，课堂练习加强运用等内容，欢迎下载使用。
知识与技能:理解三角形中位线定义与性质,会应用三角形中位线解决实际问题.过程与方法:经历探究三角形中位线定义、性质的过程，感受三角形中位线定理的应用思想。情感、态度与价值观：培养良好的探究意识和合作交流的习惯，体会数学推理的应用价值.
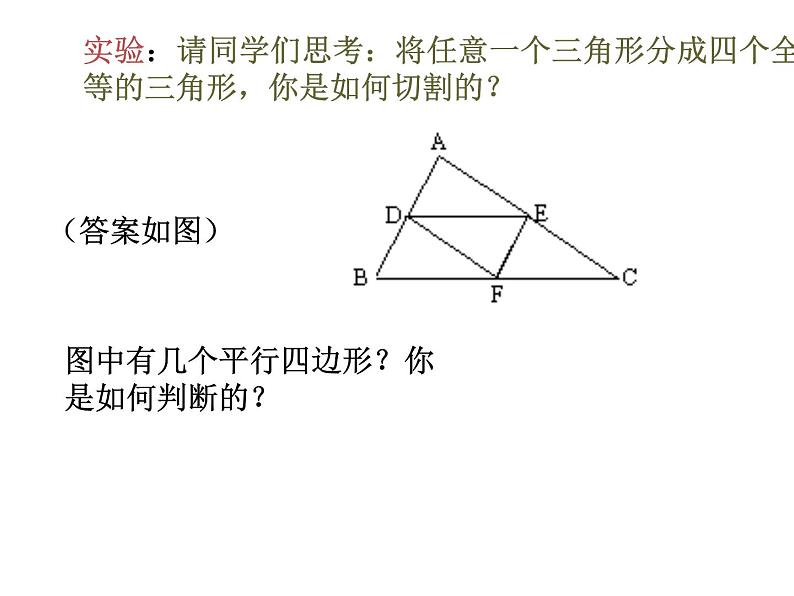
实验：请同学们思考：将任意一个三角形分成四个全等的三角形，你是如何切割的？
图中有几个平行四边形？你是如何判断的？
（连结顶点与对边中点的线段）
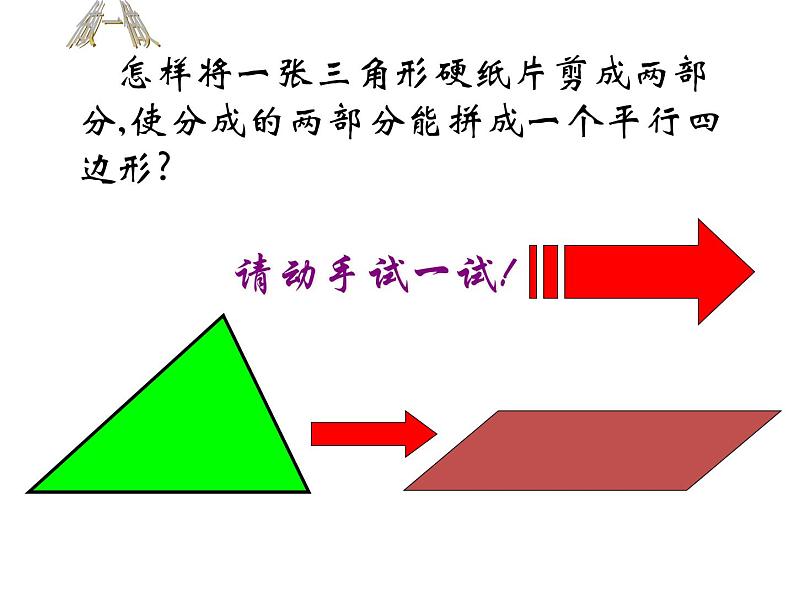
设疑：如果连结两边中点的线段呢？
连接三角形两边中点的线段叫做三角形的中位线。
画出三角形的所有中线并说出中位线和中线的区别.
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线，那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点， 那么DE为△ABC的 ；
在△ABC中，中位线DE和边BC什么关系?
结论：三角形的中位线平行于第三边，并且等于它的一半.
三角形的中位线平行于第三边，并且等于它的一半
如图1：在△ABC中，DE是中位线 （1）若∠ADE=60°， 则∠B= 度，为什么？ （2）若BC=8cm， 则DE= cm，为什么？
如图2：在△ABC中，D、E、F分别 是各边中点 AB=6cm，AC=8cm，BC=10cm， 则△DEF的周长= cm
例1求证三角形的一条中位线与第三边上的中线互相平分．
已知：　如图24．4．3所示，在△ABC中，AD＝DB，BE＝EC，AF＝FC．求证：　AE、DF互相平分．
证明连结DE、EF．∵ AD＝DB，BE＝EC，∴ DE∥AC（三角形的中位线平行于第三边并且等于第三边的一半）．同理EF∥AB．∴四边形ADEF是平行四边形．∴ AE、DF互相平分（平行四边形的对角线互相平分）．
例2如图24．4．4，△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G．求证：　
∵　D、E分别是边BC、AB的中点，
（三角形的中位线平行于第三边并且等于第三边的一半），
∴　△ACG∽△DEG，
如果在上图中，取ＡＣ的中点Ｆ，假设ＢＦ与ＡＤ交于Ｇ`，如下图，那么我们同理有，所以有 ，即两图中的点G与G`是重合的。于是我们有以下结论：三角形三条边上的中线交于一点，这个点就是三形的重心，重心与一边中点的连线的长是对应中线长的
数学上的重心与物理上的重心是一致的
1、如图：EF是△ABC 的中位线，BC=20，则EF= （ ） ;
2、在△ABC中，中线CE、BF相交点O、M、N分别是OB、OC的中点，则EF和MN的关系是( )
求证：顺次连结四边形四条边的中点所得的四边形是平行四边形。
已知：在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点. 求证：四边形EFGH是平行四边形.
证明：连结AC. ∵AH=HD，CG=GD ∴HG∥AC, HG= AC 同理 EF∥AC EF= AC ∴HG∥EF HG=EF ∴四边形EFGH是平行四边形.
测出MN的长，就可知A、B两点的距离
在AB外选一点C，使C能直接到达A和B，
连结AC和BC，并分别找出AC和BC的中点M、N.
若MN=36 m，则AB=
④顺次连结对角线相等且互相垂直的四边形四边中点所得的四边形是—————
②顺次连结对角线相等的四边形四边中点所得的四边形是————
③顺次连结对角线互相垂直的四边形四边中点所得的四边形是————
①顺次连结四边形四边中点所得的四边形是———————
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系，而且给出了他们的数量关系，在三角形中给出一边的中点时，要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方法（包括画图、实验、猜想、分析、归纳等.)
①顺次连结平行四边形四边中点所得的四边形是————————
②顺次连结等腰梯形四边中点所得的四边形是——————
③顺次连结矩形四边中点所得的四边形是——————
④顺次连结菱形四边中点所得的四边形是——————
⑤顺次连结正方形四边中点所得的四边形是—————
3.已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△HPN的周长等于——————,为△ABC周长的——, 面积为△ABC面积的——,
2.已知:三角形的各边分别为6cm,8cm, 10cm，则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。
∠B —— ∠ADE(填“=”或“≠”)
4.如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则DP= ———，BC= ———
BC=CD，则顺次连结它的各边中点得到的四边形是（ ）
5.在四边形ABCD中，AB=AD，
6.已知:E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连结AE,分别交BC、BD于点F、G，连接AC交BD于O，连结OF.求证: AB= 2 OF
提示:证明△ABF≌ △ECF, 得BF=CF,再证OF是△ABC的中位线.