2021学年23.4 中位线教学课件ppt

这是一份2021学年23.4 中位线教学课件ppt，共21页。PPT课件主要包含了新课导入，设计方案，概念对比，中线DC，中位线DE，三角形中位线定理，证明连结ED，典例示范等内容，欢迎下载使用。
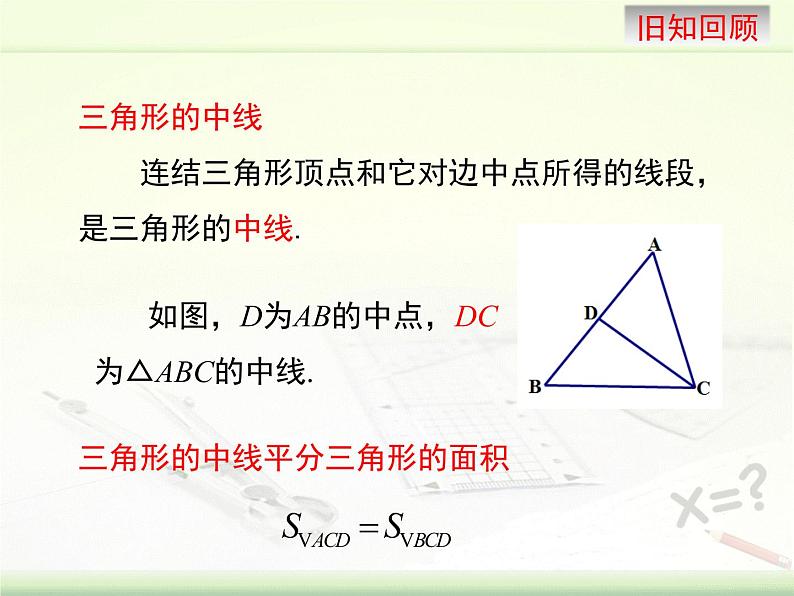
三角形的中线 连结三角形顶点和它对边中点所得的线段，是三角形的中线.
如图，D为AB的中点，DC为△ABC的中线.
三角形的中线平分三角形的面积
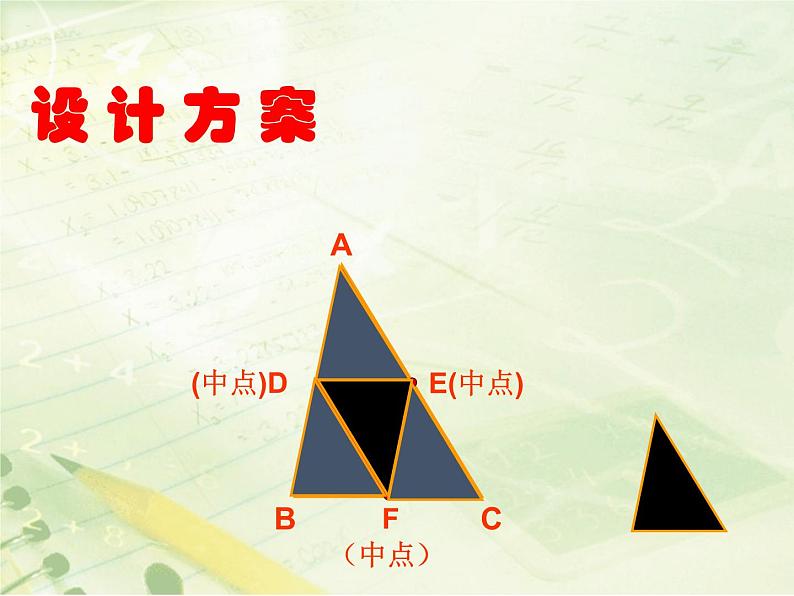
如图，有一块三角形的蛋糕，准备平均分给四个小朋友，要求四人所分的形状大小相同，请设计合理的解决方案。
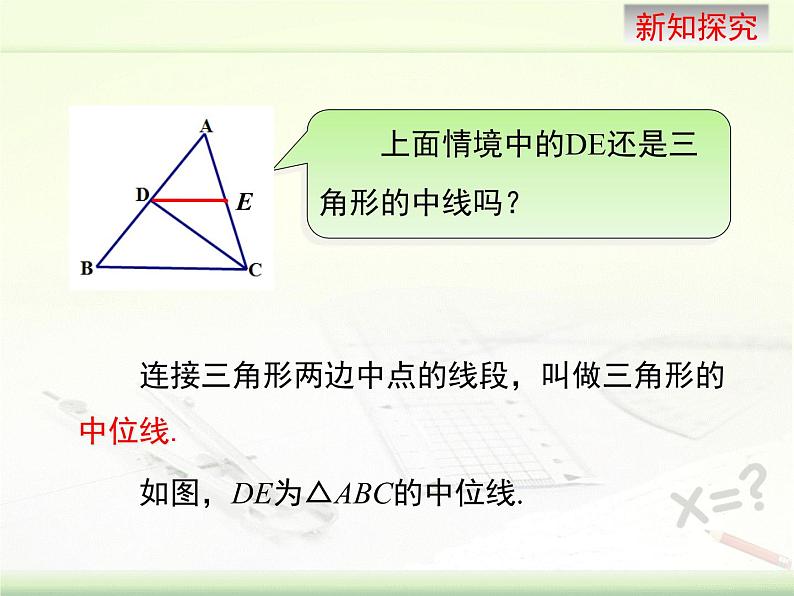
如图，DE为△ABC的中位线.
连接三角形两边中点的线段，叫做三角形的中位线.
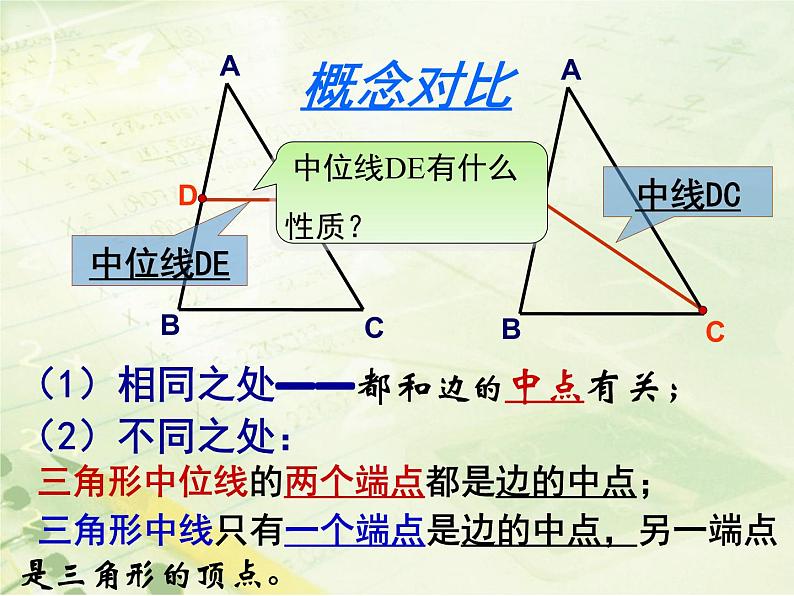
（1）相同之处——都和边的中点有关；（2）不同之处： 三角形中位线的两个端点都是边的中点； 三角形中线只有一个端点是边的中点，另一端点是三角形的顶点。
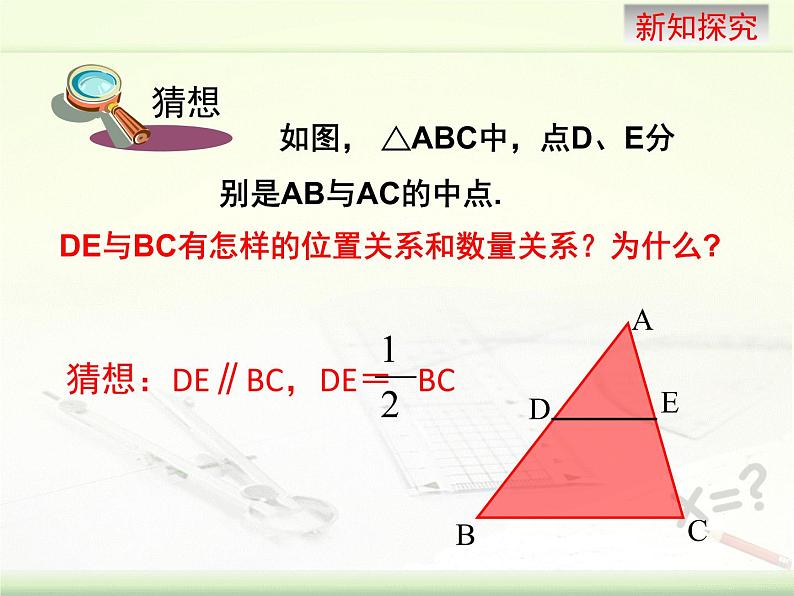
如图， △ABC中，点D、E分别是AB与AC的中点.
DE与BC有怎样的位置关系和数量关系？为什么?
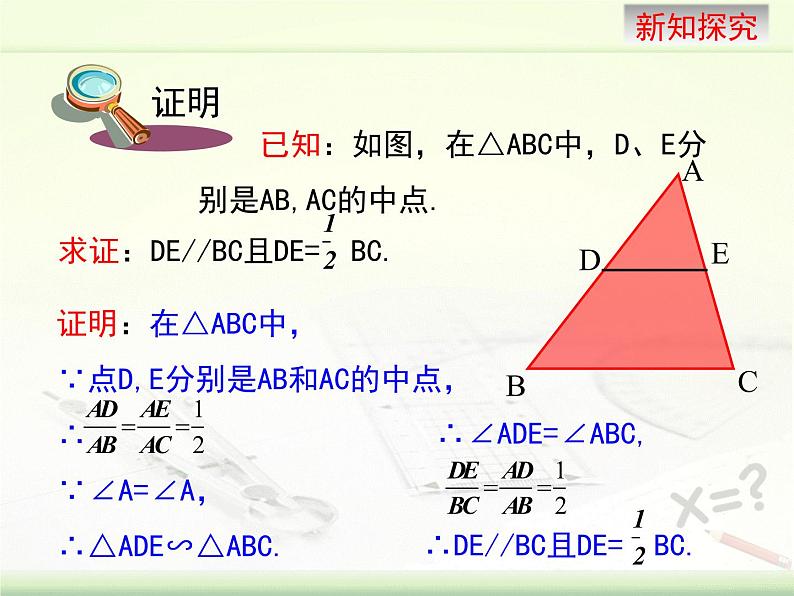
证明：在△ABC中，∵点D,E分别是AB和AC的中点，∴∵∠A=∠A，∴△ADE∽△ABC.
已知：如图，在△ABC中，D、E分别是AB,AC的中点.
∴∠ADE=∠ABC,
∵EF是△ABC的中位线.
如图，A、B两棵树被池塘隔开，现在要测量出A、B两树间的距离 ，但又无法直接去测量，怎么办？
∵DE是△ABC的的中位线,∴AB=2DE.
如图，在△ABC中，D、E分别是AB、AC的中点
1.若∠ADE=65°，则∠B= 度
2.若BC=8cm，则DE= cm
3.若AC=4cm,BC=6cm，AB=8cm， 则△DEF的周长=______
4.若△ABC的周长为24，△DEF的周长是_____
5.若△ABC的面积为24，△DEF的面积是_____
例1 已知：如图所示，在△ABC中，AD＝DB，BE＝EC，AF＝FC． 证明: AE、DF互相平分
解：连接DE、EF∵ AD＝DB，BE＝EC，∴ DE∥AC.同理EF∥AB．∴四边形ADEF是平行四边形．∴AE、DF互相平分
例2 如图所示， △ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G，求证：
∵D、E分别是边BC、AB的中点，
∴△ACG∽△DEG，
如果在右图中，取AC的中点F，假设BF与AD交于G′，那么，可得，
即两图中的点G与G′是重合的．
E，F是AB，BC的中点，你联想到什么？
要使EF成为一个三角形的中位线应怎样添加辅助线？
∵EF是△ABC的中位线
∴四边形EFGH是平行四边形
答： 四边形EFGH为平行四边形。
2.如图，E,F,G,H分别是AB、BC、CD、DA的中点.求证: (1)四边形EFGH是平行四边形.
(2)请增加一个条件使得四边形EFGH为菱形.(3) 请增加一个条件使得四边形EFGH为矩形.
(4)能不能只增加一个条件使得四边形EFGH为正方形.
定义 连结三角形两边中点的线段叫做三角形的中位线.
性质 三角形的中位线平行于第三边,并且等于第三边的一半.