苏科版八年级上册3.1 勾股定理练习题

第3章    勾股定理（自主检测）（基础卷）

一．选择题（每小题2分，共12分）

1.以下列各组数为边长，能组成直角三角形的是（   ）

A．2，3，4 B．10，8，4 C．7，25，24 D．7，15，12

【答案】C

【解析】解：A、∵22+32≠42，∴不能构成直角三角形，故本选项错误；

B、∵42+82≠102，∴不能构成直角三角形，故本选项错误；

C、∵72+242=252，∴能构成直角三角形，故本选项正确；

D、∵72+122≠152，∴不能构成直角三角形，故本选项错误．

故选C．

2.下列条件中，不能断定△ABC为直角三角形的是（    ）

A． B．

C． D．

【答案】D

【解析】解：A项，因为，符合勾股定理的逆定理，正确；

B项，因为，，所以，所以△ABC为直角三角形，正确；

C项，因为，所以设a=3x，b=4x，c=5x，则（3x）2+（4x）2=（5x）2，所以△ABC为直角三角形，正确；

D项，因为，可设，所以，解得，，故此三角形是锐角三角形，错误；

故选D.

3.如图，为修铁路需凿隧道，测得，，，若每天凿隧道，则把隧道凿通需要（ ）

A．10天 B．天 C．天 D．天

【答案】A

【解析】解：∵∠A+∠B=90°，AB=130m，BC=120m，

∴

∵每天凿隧道5m，

∴ 50÷5=10=10（天）．

故选A．

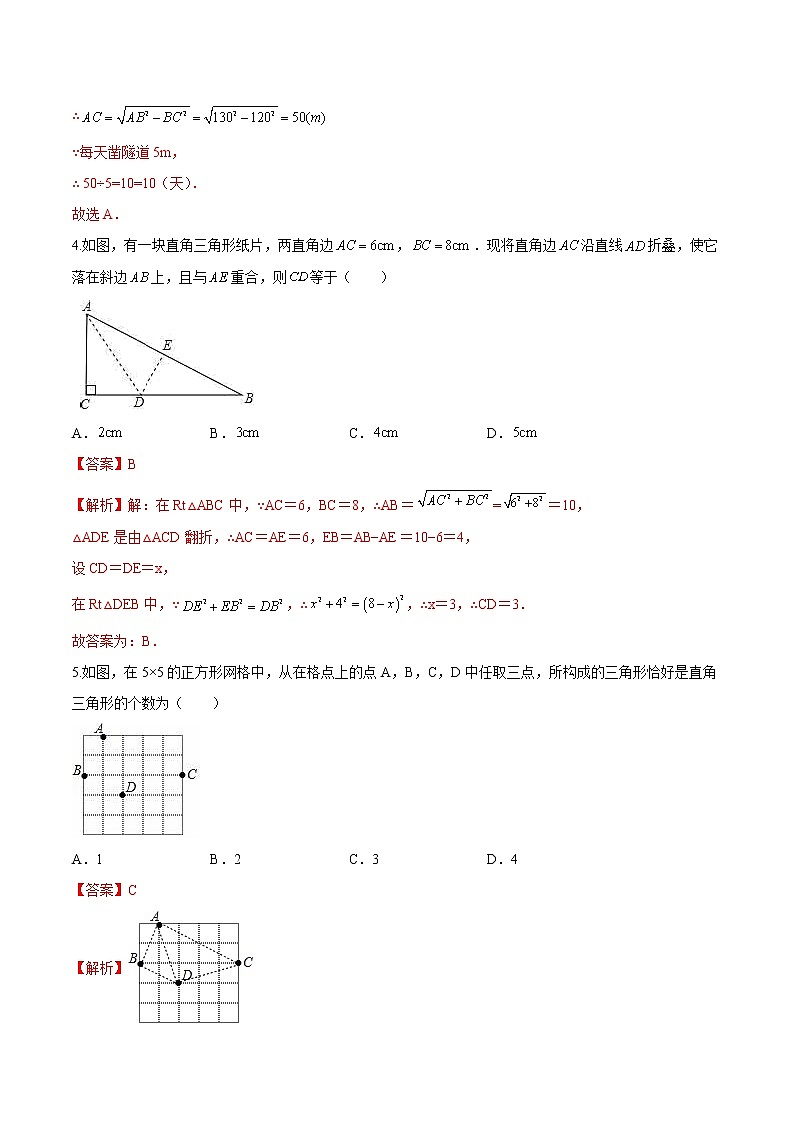
4.如图，有一块直角三角形纸片，两直角边，．现将直角边沿直线折叠，使它落在斜边上，且与重合，则等于（　　）

A． B． C． D．

【答案】B

【解析】解：在Rt△ABC中，∵AC＝6，BC＝8，∴AB＝=＝10，

△ADE是由△ACD翻折，∴AC＝AE＝6，EB＝AB−AE＝10−6＝4，

设CD＝DE＝x，

在Rt△DEB中，∵，∴，∴x＝3，∴CD＝3．

故答案为：B．

5.如图，在5×5的正方形网格中，从在格点上的点A，B，C，D中任取三点，所构成的三角形恰好是直角三角形的个数为（　　）

A．1 B．2 C．3 D．4

【答案】C

【解析】

理由是：连接AC、AB、AD、BC、CD、BD，

设小正方形的边长为1，

由勾股定理得：AB2=12+22=5,AC2=22+42=20,AD2=12+32=10,BC2=52=25,CD2=12+32=10,BD2=12+22=5，

∴AB2+AC2=BC2,AD2+CD2=AC2,BD2+AB2=AD2，

∴△ABC、△ADC、△ABD是直角三角形，共3个直角三角形，

故选C.

6.已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB=3，则图中阴影部分的面积为( )

 

A． B．3 C． D．9

【答案】A

【解析】由题意得，三个等腰直角三角形的是以Rt△ABC的三边为边作正方形的四分之一，因在Rt△ABC中，AB=3，AB2=AC2+BC2=9，所以三个正方形的面积和为18，即可得阴影部分面积为，故选A.

二．填空题（每小题2分，共20分）

7.如图中阴影部分是一个正方形，如果正方形的面积为64厘米2  ， 则x的长为________厘米．

【答案】17

【解析】解:正方形的面积为64, 正方形的边长为:8, 

则x的长为:

8.中，斜边BC＝2，则AB2+AC2+BC2的值为_____．

【答案】8

【解析】∵中，BC为斜边，且，

∴，

∴，

故答案为：8．

9.将一根24 cm的筷子，置于底面直径为15 cm，高8 cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度为h cm，则h的取值范围是___________．

【答案】7cm≤h≤16cm．

【解析】解：如图，当筷子的底端在D点时，筷子露在杯子外面的长度最长，

∴h=24-8=16cm；
当筷子的底端在A点时，筷子露在杯子外面的长度最短，
在Rt△ABD中，AD=15，BD=8，

∴此时h=24-17=7cm，
所以h的取值范围是7cm≤h≤16cm．
故答案为7cm≤h≤16cm．

10.如图，每个小方格都是边长为1的正方形，点，是方格纸的两个格点（即正方形的顶点）.在这张的方格纸中，找出格点，使为面积为1的直角三角形，则点的个数是________.

【答案】6

【解析】解：因为，，所以点距线段的距离为1.

如图，当为直角时，满足条件的点是，；

当为直角时，满足条件的点是，；

当为直角时，满足条件的点是，。

所以满足条件的点共有6个.

11.如图，某港口P位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行12nmile，“海天”号每小时航行9nmile，它们离开港口两个小时后分别位于点Q，R处，且相距30nmile．如果知道“远航”号沿北偏东50°方向航行，那么“海天”号沿______的方向航行．

【答案】北偏西40°

【解析】解：∵“远航”号每小时航行12nmile，“海天”号每小时航行9nmile，

∴，，∵两船相距30nmile，∴，

∵，∴，∴∠QPR=90°，

∵“远航”号沿北偏东50°方向，∴∠NPQ=50°，

∴∠NPR=90°－50°=40°，∴“海天”号沿北偏西40°方向航行，故答案为：北偏西40°．

12.在△ABC中，若AC2＋BC2＝AB2，∠A∶∠B＝1∶2，则∠B的度数是________．

【答案】60°

【解析】在△ABC中，因为AC2＋BC2＝AB2,

所以△ABC是以AB为斜边的直角三角形,则∠C=90°,所以∠A+∠B=90°，

因为∠A:∠B＝1:2,所以∠B=90°×60°.

故答案为:60°.

13.如图，已知中，，，，是的垂直平分线，交于点，连接，则___

【答案】5

【解析】解：∵是的垂直平分线，∴AD=CD，∴∠CAD=∠ACD

∵，，

又∵ ，∴ ，∴∠ACB=90°

∵∠ACD+∠DCB=90°, ∠CAB+∠B=90°，∴∠DCB=∠B

∴CD=BD，∴CD=BD=AD=

故答案为5

14.一个透明的圆柱形的玻璃杯，测得其底面半径为3cm，高为8cm，今有一根长度为12cm的细吸管斜放在杯子中，则吸管露出杯口外的长度最少为________.

【答案】2cm

【解析】如下图所示：

∵底面半径为3厘米，高为8厘米，∴AC=6厘米，BC=8厘米，

∴AB= =10厘米，∴杯口外的长度最小为：12−10=2(厘米).

故答案为2cm.

15.已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB＝3,则图中阴影部分的面积为   __________.

【答案】4.5

【解析】本题考查的是勾股定理的应用．由题意得三个等腰直角三角形的是以Rt△ABC的三边为边作正方形的四分之一而三个正方形的面积和为18，故阴影部分面积为．

16.如图所示，等腰三角形ABC的底边为8cm，腰长为5cm ，一动点P（与B、C不重合）在底边上从B向C以1cm/s的速度移动，当P运动____________秒时，△ACP是直角三角形

【答案】1.75或4

【解析】解：如图，作AD⊥BC，∵AB=AC=5cm，BC=8cm，∴BD=CD=4cm，

当点P运动到与点D重合时，是直角三角形，此时BP=4，∴运动时间为4÷1=4（秒）；

当∠PAC=90°时，设PD=x∴，

又∵，∴，∴，

∴BP=4－2.25=1.75，所以运动时间为1.75÷1=1.75（秒）；

综上可得：当P运动4秒或1.75秒时，是直角三角形；故答案为：1.75或4．

三．解答题（共68分）

17.（10分）如图，在中，，，是上一点，，．

（1）求证：；（2）求的长．

【答案】（1）见解析；（2）的长为．

【解析】（1）证明：，，

，，；

（2）设，则，

在中，，，，

解得，的长为．

18.（8分）如图，在中，是上的一点，若，，，，求的面积．

【答案】84

【解析】解：，

是直角三角形，，

在中，，，

．因此的面积为84．

故答案为84．

19.（10分）如图是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为和，斜边长为．图是以为直角边的等腰直角三角形．请你开动脑筋，将它们拼成一个能证明勾股定理的图形．

【答案】见解析.

【解析】解：如图：

梯形的面积，

整理得．

20.（10分）如图，梯子长25米，斜靠在一面墙上，梯子底端离墙7米．

（1）这个梯子的顶端距地面有多高？

（2）如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？

【答案】（1）24米； （2）8米．

【解析】（1）根据题意得，

∴梯子顶端距地面的高度米；

 （2）=米，

∵∴根据勾股定理得，米，

∴米，

答：梯子下端滑行了8米．

21.（10分）如图，正方形网格中，小格的顶点叫做格点，按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形．小华在下边的正方形网格中作出了．

（1）你认为小华作出的是直角三角形吗?请给予说明；

（2）请你按照同样的要求，在上边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等．

【答案】（1）是，证明见解析；（2）见解析

【解析】（1）是直角三角形，

∵，，

，

∴，

∴是直角三角形；

（2）作图如下，答案不唯一．

22.（10分）如图，有一艘货船和一艘客船同时从港口A出发，客船每小时比货船多走5海里，客船与货船速度的比为4：3，货船沿东偏南10°方向航行，2小时后货船到达B处，客船到达C处，若此时两船相距50海里．

（1）求两船的速度分别是多少？

（2）求客船航行的方向．

【答案】（1）两船的速度分别是20海里/小时和15海里/小时；（2）客船航行的方向为北偏东10°方向．

【解析】（1）设两船的速度分别是4x海里/小时和3x海里/小时，依题意得：4x﹣3x=5．

解得：x=5，∴4x=20，3x=15．

答：两船的速度分别是20海里/小时和15海里/小时；

（2）由题可得：AB=15×2=30，AC=20×2=40，BC=50，∴AB2+AC2=BC2，∴△ABC是直角三角形，且∠BAC=90°．

又∵货船沿东偏南10°方向航行，∴∠1=10°．

∵∠1+∠2=∠2+∠3=90°，∴∠3=∠1=10°，∴客船航行的方向为北偏东10°方向．

23.（10分）台风是一种自然灾害，它以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力，有一台风中心沿东西方向AB由点A行驶向点B，已知点C为一海港，且点C与直线AB上两点A、B的距离分别为300km和400km，又AB＝500km，以台风中心为圆心周围250km以内为受影响区域．

（1）海港C会受台风影响吗？为什么？

（2）若台风的速度为20km/h，台风影响该海港持续的时间有多长？

【答案】（1）会，理由见解；（2）7h

【解析】解：（1）如图所示，过点C作CD⊥AB于D点，

∵AC=300km，BC=400km，AB=500km，

∴，∴△ABC为直角三角形，

∴，∴，∴，

∵以台风中心为圆心周围250km以内为受影响区域，

∴海港C会受到台风影响；

（2）由（1）得CD=240km，

如图所示，当EC=FC=250km时，即台风经过EF段时，正好影响到海港C，

此时△ECF为等腰三角形，

∵，∴EF=140km，

∵台风的速度为20km/h，∴140÷20=7h，

∴台风影响该海港持续的时间有7h．