数学七年级上册第四章 基本平面图形综合与测试习题ppt课件

这是一份数学七年级上册第四章 基本平面图形综合与测试习题ppt课件，共40页。PPT课件主要包含了答案呈现，习题链接，直线AC等内容，欢迎下载使用。
下列说法正确的是(　　)A．直线AC与直线CA是不同的直线B．射线AB与射线BA是同一条射线C．线段AB与线段BA是同一条线段D．直线AD＝AB＋BC＋CD
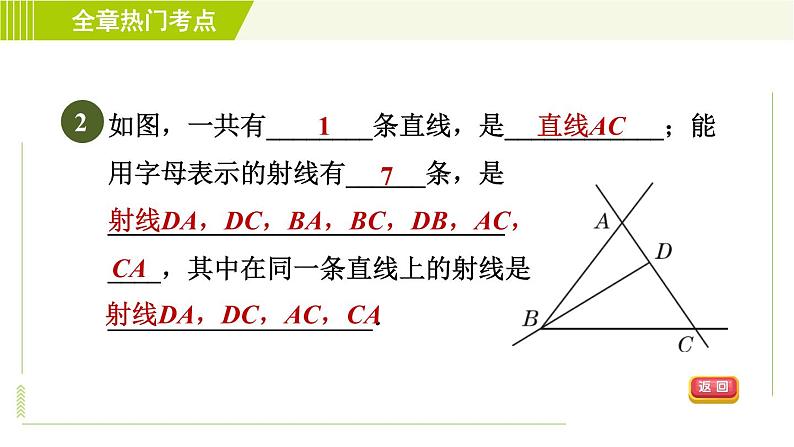
如图，一共有________条直线，是____________；能用字母表示的射线有______条，是__________________________________，其中在同一条直线上的射线是____________________．
射线DA，DC，BA，BC，DB，AC，
射线DA，DC，AC，CA
如图，以B为顶点的角有几个？把它们表示出来．以D为顶点的小于平角的角有几个？把它们表示出来．
解：以B为顶点的角有3个，分别是∠ABD，∠ABC，∠DBC.以D为顶点的小于平角的角有4个，分别是∠ADE，∠EDC，∠ADB，∠BDC.
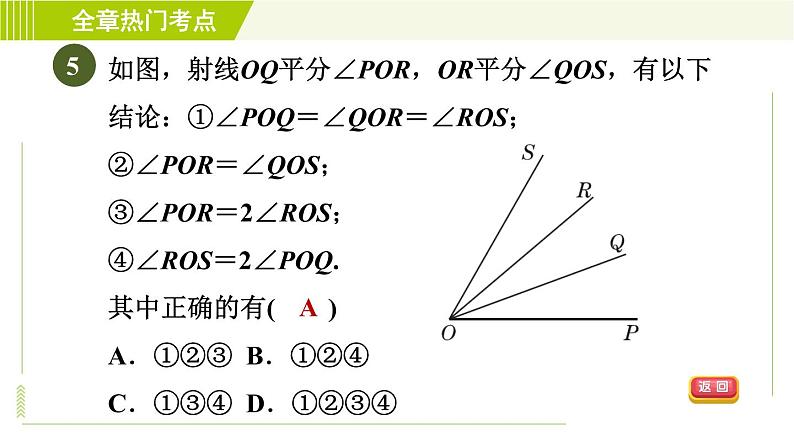
如图，射线OQ平分∠POR，OR平分∠QOS，有以下结论：①∠POQ＝∠QOR＝∠ROS；②∠POR＝∠QOS；③∠POR＝2∠ROS；④∠ROS＝2∠POQ.其中正确的有(　　)A．①②③ B．①②④C．①③④ D．①②③④
下列属于正n边形的特征的有(　　)①各边相等；②各个内角相等；③各条对角线都相等；④从一个顶点可以引(n－2)条对角线；⑤从一个顶点引出的对角线将正n边形分成面积相等的(n－2)个三角形．A．2个 B．3个 C．4个 D．5个
下列说法正确的是(　　)A．由不在同一直线上的几条线段相连所组成的封闭图形叫做多边形B．一条弧和经过弧的两条半径围成的图形叫做扇形C．三角形是最简单的多边形D．圆的一部分是扇形
下列现象可以用“两点确定一条直线”来解释的有(　　)①墙上钉木条至少要钉两个钉子才能牢固；②农民拉绳插秧；③解放军叔叔打靶瞄准；④从A地到B地架设电线，总是尽可能沿着线段AB架设．A．1个 B．2个 C．3个 D．4个
下列现象中，可用基本事实“两点之间，线段最短”来解释的是(　　)A．用两个钉子就可以把木条固定在墙上B．把弯曲的公路改直，就能缩短路程C．利用圆规可以比较两条线段的长短关系D．植树时，只要定出两棵树的位置，就能确定同一行树所在的直线
如图，已知线段AD＝10 cm，点B，C都是线段AD上的点，且AC＝7 cm，BD＝4 cm.若点E，F分别是线段AB，CD的中点，求线段EF的长．
如图，O是直线AB上一点，OC，OD是从O点引出的两条射线，OE平分∠AOC，∠BOC：∠AOE：∠AOD＝2：5：8，求∠BOD的度数．
解：设∠BOC＝2x°，则∠AOE＝5x°，∠AOD＝8x°.因为O是直线AB上一点，所以∠AOB＝180°.
所以∠COE＝(180－7x)°.因为OE平分∠AOC，所以∠AOE＝∠COE，即5x＝180－7x，解得x＝15.所以∠AOD＝8×15°＝120°.所以∠BOD＝60°.
如图，把一个圆分成四个扇形，请分别求出这四个扇形的圆心角的度数．若该圆的半径为2 cm，请分别求出它们的面积．
解：扇形AOB的圆心角为360°×35%＝126°，扇形BOC的圆心角为360°×10%＝36°，扇形COD的圆心角为360°×25%＝90°，扇形AOD的圆心角为360°×30%＝108°.
因为圆的面积为π×22＝4π(cm2)，所以S扇形AOB＝4π×35%＝1.4π(cm2)，S扇形BOC＝4π×10%＝0.4π(cm2)，S扇形COD＝4π×25%＝π(cm2)，S扇形AOD＝4π×30%＝1.2π(cm2)．
如图，平面内有过公共端点O的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写上数1，2，3，4，5，6，7，….(1)数“17”在射线________上；
(2)请任意写出三条射线上数的排列规律；
解：(任意写出三条射线上数的排列规律即可)射线OA上数的排列规律：6n－5(n为正整数)．射线OB上数的排列规律：6n－4(n为正整数)．射线OC上数的排列规律：6n－3(n为正整数)．射线OD上数的排列规律：6n－2(n为正整数)．射线OE上数的排列规律：6n－1(n为正整数)．射线OF上数的排列规律：6n(n为正整数)．
(3)数“2 022”在哪条射线上？
解：因为2 022÷6＝337，所以数“2 022”在射线OF上．
从下午2时15分到下午5时30分，时钟的时针转了多少度？
解：由题意知，时针走的大格数为5.5－2.25.因此时针转的角度为30°×(5.5－2.25)＝97.5°.故从下午2时15分到下午5时30分，时钟的时针转了97.5°.
如图，C，D，E将线段AB分成2：3：4：5的四部分，M，P，Q，N分别是AC，CD，DE，EB的中点，且MN＝21，求线段PQ的长度．
【点拨】解答此题的关键是设出未知数，利用线段长度的比及中点建立方程，求出未知数的值，进而求解，体现了转化思想在解题中的应用．
已知线段AB＝12 cm，直线AB上有一点C，且BC＝6 cm，M是线段AC的中点，求线段AM的长．
已知一条射线OA，若从点O引两条射线OB，OC，使∠AOB＝60°，∠BOC＝20°，求∠AOC的度数．
解：当OC在∠AOB的内部时，如图①，∠AOC＝∠AOB－∠BOC＝60°－20°＝40°.
当OC在∠AOB的外部时，如图②，∠AOC＝∠AOB＋∠BOC＝60°＋20°＝80°.综上可知，∠AOC的度数为40°或80°.
如图，OM，OB，ON是∠AOC内的三条射线，OM，ON分别是∠AOB，∠BOC的平分线，∠NOC是∠AOM的3倍，∠BON比∠MOB大30°，求∠AOC的度数．
解：设∠AOM＝x，则∠NOC＝3x.因为OM，ON分别是∠AOB，∠BOC的平分线，所以∠MOB＝∠AOM＝x，∠BON＝∠NOC＝3x.依题意得3x－x＝30°，解得x＝15°，即∠AOM＝15°，所以∠MOB＝15°，∠BON＝∠NOC＝45°.所以∠AOC＝∠AOM＋∠MOB＋∠BON＋∠NOC＝15°＋15°＋45°＋45°＝120°.
两人开车从A市到B市要走一天，计划上午比下午多走100 km到C市吃饭，由于堵车，中午才赶到一个小镇，只行驶了原计划的三分之一，过了小镇汽车赶了400 km，傍晚才停下休息，一人说，再走从C市到这里路程的二分之一就到达目的地了，问A，B两市相距多少千米？