初中数学北师大版八年级上册1 平均数获奖ppt课件

这是一份初中数学北师大版八年级上册1 平均数获奖ppt课件，文件包含611《平均数》课件pptx、611《平均数》同步练习docx、611《平均数》教学设计教案doc等3份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

1、掌握算术平均数和加权平均数的概念，会求一组数据的算术平均数和加权平均数.2、能说出“权”的差异，对平均数的影响，算术平均数和加权平均数的区别.3、利用算数平均数和加权平均数解决一些实际问题，进一步增强统计意识和数学应用的能力。
教学重点： 平均数的计算（包括加权平均数）。教学难点：能用平均数的计算（包括加权平均数），解决较复杂的实际问题。
第六章数据的收集与整理 6.1 数据的收集. 6.2 普查与抽样调查 6.3 数据的表示 6.4 统计图的选择
第六章数据的分析 6.1 平均数. 6.2 中位数与众数 6.3 数据的集中趋势 6.4 数据的离散程度
生活中，人们离不开数据，我们不仅要收集、整理和表示数据，还要对数据进行分析，进而帮我们更好地作出判断. 我们常用平均数、中位数、众数描述数据的集中趋势，用方差、极差等描述数据的波动程度.
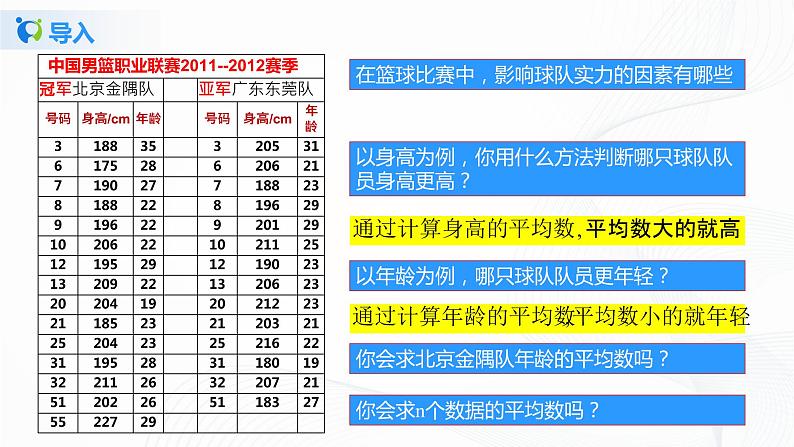
在篮球比赛中，影响球队实力的因素有哪些？
以身高为例，你用什么方法判断哪只球队队员身高更高？
以年龄为例，哪只球队队员更年轻？
你会求北京金隅队年龄的平均数吗？
你会求n个数据的平均数吗？

例1: 不久前同学们进行了期中考试，我想估计我们班数学平均成绩，随机抽取了班中6名同学的分数，接下来我该怎么办？ 83 78 65 99 54 89
（1）78是83，78，…，89的算术平均数.
（简单）算术平均数
平均数作为一组数据的一个代表值它刻画了这组数据的平均水平.
问题2：我想进一步估计年级每人数学的平均成绩，抽取每班部分同学的平均分和相应的人数，接下来该怎么办？
问题3：两位同学的算法哪一个正确？为什么？
数据的权（weight）能反映数据的相对“重要程度”.
（2）75.8是70,78，…，68的加权平均数, 其中 5，10，…，6分别是70,78，…，68的权.
例2 一家公司打算招聘一名英文翻译，对甲、乙两名应试者进行了听、说、读、写（1）如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照3∶3∶2∶2的比确定，计算两名应试者的平均成绩（百分制）.从他们写的英语水平测试应该录取谁？
（2）如果现在要招一名笔译能力较强的翻译，你能给各数据制定一个合适的权吗？制定的依据是什么？分组讨论并计算答案.
解：（1）听、说、读、写的成绩按照3∶3∶2∶2的比确定，则甲的平均成绩为
85×3＋83×3＋78×2＋75×2 3＋3＋2＋2
73×3＋80×3＋85×2＋82×2 3＋3＋2＋2
显然甲的成绩比乙的高，所以从成绩看，应该录取甲．
问题：平均数与加权平均数之间有什么关系？
加权平均数是平均数的推广，平均数是加权平均数的特例；当所有权数都相等(都等于数据组所含数据的数目的倒数)时，加权平均数与平均数一致.
例3 一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分，各项成绩均按百分制， 然后再按演讲内容占50％、演讲能力占40％、演讲效果占10％的比例，计算选手的综合成绩（百分制）．进入决赛的前两名选手的单项成绩.如下表所示：
思考（2）利用加权平均数公式你能求出A、B的综合 成绩，决出两人的名次，验证你的猜想.
思考（1）能先猜出两人的名次吗，依据是什么？
解（1）B取第一名，B演讲内容的成绩高，它的权相对较大. （2）A的综合成绩为 85×50%+95×40%+95×10%=90 B的综合成绩为 95×50%+85×40%+95×10%=91 B的成绩高于A的成绩，B取第一名，A取第二名.
1. 数据出现的次数的形式.如31,32,28；2. 比例的形式. 如3:3:2:2；3. 百分数形式. 如50%，40%，10%.
1. 学校举行运动会，入场式中有七年级的一个队列.已知这个队列共100人，排成10行，每行10人，其中前两排同学的身高都是160cm，接着的三排同学的身高是155cm，其余五排同学的身高是150cm.求这个队列的同学的平均身高.
答： 160×0.2+155×0.3+150×0.5 = 153.5(m).
2. 商店中有3种糖果，各种糖果的单价如下表所示：
答: 11.6×0.2+14.4×0.3+16×0.5 = 14.64(元).
商店用水果糖20kg、花生糖30kg、软糖50kg配成什锦糖100kg，问这100kg什锦糖的单价应如何确定？
3. 用两种方法计算下列数据的平均数： 35， 35， 34， 47， 47，84， 84， 84， 84，125. (1)一般方法; (2) 加权平均法.
4. 学校举行元旦文艺演出，由参加演出的10个班各推选一名同学担任评委袁，每个节目演出后的得分为各评委所给分的平均数. 下面是各评委对某班演出节目给出的分数：
5.下表是小红和小明参加一次演讲比赛的得分情况：
评总分时，按服装占5%，普通话占15%，主题占40%，演讲技巧占40%考评，你认为小红和小明谁更优秀？
6、解：(1)一班平均成绩 ×(95＋90＋90＋85)＝90二班平均成绩 ×(90＋95＋85＋90)＝90三班平均成绩 ×(85＋90＋95＋90)＝90各班平均成绩相等，卫生状况一样．90×40%＝91
(2)一班平均成绩：95×15%＋90×10%＋90×35%＋85×40%＝88.75二班平均成绩：90×15%＋95×10%＋85×35%＋90×40%＝88.75三班平均成绩：85×15%＋90×10%＋95×35%＋90×40%＝91∴三班的卫生成绩较高．
一、加权平均数的计算公式公式：
二、权的常见形式：1、比的形式：如 3:3:2:22、百分比形式：如30％、30％、20％、20％
三、加权平均数与算术平均数的关系算术平均数是加权平均数的特例
1、算术平均数的概念2、算术平均数的公式3、加权平均数的概念4、加权平均数的公式
1、八年级（1）班有学生50人，八年级（2）班有学生45人，期末数学测试中，（1）班学生的平均分为81.5分，（2）班学生的平均分为83.4分，这两个班95名学生的平均分是多少？
2、为考察甲、乙两种农作物的长势，研究人员分别抽取了10株苗，测得它们的高度如下（单位：cm）如下：甲：9，14，11，12，9，13，10，8，12，8； 乙：8，13，12，11，9，12，7，7，9，11你认为哪种农作物长得高一些？说说理由．