第3章 第2节 第1课时 导数与函数的单调性-2022届高三数学一轮复习讲义(新高考)教案
展开
这是一份第3章 第2节 第1课时 导数与函数的单调性-2022届高三数学一轮复习讲义(新高考)教案,共15页。教案主要包含了教材概念·结论·性质重现,基本技能·思想·活动体验等内容,欢迎下载使用。
一、教材概念·结论·性质重现
导数与函数的单调性的关系
若函数f (x)在区间(a,b)上单调递增,则f ′(x)≥0,“f ′(x)>0在区间(a,b)上成立”是“f (x)在区间(a,b)上单调递增”的充分不必要条件.
二、基本技能·思想·活动体验
1.判断下列说法的正误,对的打“√”,错的打“×”.
(1)若函数f (x)在区间(a,b)上单调递增,那么一定有f ′(x)>0.(×)
(2)如果函数f (x)在某个区间内恒有f ′(x)=0,则f (x)在此区间内不具有单调性.(√)
(3)若在区间(a,b)内f ′(x)≤0且f ′(x)=0的根为有限个,则f (x)在区间(a,b)内是减函数.(√)
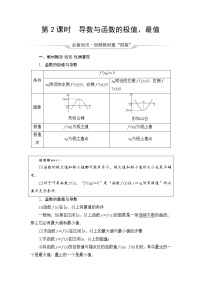
2.函数y=f (x)的导函数y=f ′(x)的图象如图所示,则函数y=f (x)的图象可能是( )
D 解析:由导函数的图象可知函数在(-∞,0)上是先减后增,在(0,+∞)上先增后减再增.故选D.
3.函数f (x)=x3-3x+1的单调递增区间是( )
A.(-1,1) B.(-∞,1)
C.(-1,+∞) D.(-∞,-1),(1,+∞)
D 解析:f ′(x)=3x2-3.由f ′(x)>0得x1.故函数f (x)=x3-3x+1的单调递增区间是(-∞,-1),(1,+∞).故选D.
4.已知函数f (x)=eq \f(ln x,x),则( )
A.f (2)>f (e)>f (3) B.f (3)>f (e)>f (2)
C.f (3)>f (2)>f (e) D.f (e)>f (3)>f (2)
D 解析:f (x)的定义域是(0,+∞).
因为f ′(x)=eq \f(1-ln x,x2),
所以x∈(0,e)时,f ′(x)>0;
x∈(e,+∞)时,f ′(x)f (3)>f (2).
5.若函数f (x)=sin x+kx在(0,π)上是增函数,则实数k的取值范围为________.
[1,+∞) 解析:因为f ′(x)=cs x+k≥0,所以k≥-cs x,x∈(0,π)恒成立.
当x∈(0,π)时,-10,解得x>eq \f(1,2),所以函数y=4x2+eq \f(1,x)的单调递增区间为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),+∞)).故选B.
2.函数y=eq \f(1,2)x2-ln x的单调递减区间为( )
A.(-1,1) B.(0,1)
C.(1,+∞)D.(0,+∞)
B 解析:y=eq \f(1,2)x2-ln x,y′=x-eq \f(1,x)=eq \f(x2-1,x)=eq \f(x-1x+1,x)(x>0).
令y′eq \f(f \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4))),cs \f(π,4)),
即f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))>eq \f(\r(6),2)f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4))),故A错误;
又f (0)=0,所以g(0)=eq \f(f 0,cs 0)=0,所以g(x)=eq \f(f x,cs x)≤0在eq \b\lc\[\rc\)(\a\vs4\al\c1(0,\f(π,2)))上恒成立.
因为ln eq \f(π,3)∈eq \b\lc\[\rc\)(\a\vs4\al\c1(0,\f(π,2))),
所以f eq \b\lc\(\rc\)(\a\vs4\al\c1(ln \f(π,3)))eq \f(π,6),所以geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))>geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3))),
所以eq \f(f \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6))),cs \f(π,6))>eq \f(f \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3))),cs \f(π,3)),
即f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))>eq \r(3)f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3))),故C正确;
因为eq \f(π,3)>eq \f(π,4),所以geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))>geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3))),
所以eq \f(f \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4))),cs \f(π,4))>eq \f(f \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3))),cs \f(π,3)),
即f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))>eq \r(2)f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3))),故D正确.
故选CD.
利用导数比较大小的方法
利用导数比较大小,其关键在于利用题目条件中的不等关系构造辅助函数,并得到辅助函数的单调性,进而根据单调性比较大小.
考向3 利用导数求参数的取值范围
已知函数f (x)=ln x,g(x)=eq \f(1,2)ax2+2x(a≠0).
(1)若函数h(x)=f (x)-g(x)存在单调递减区间,求a的取值范围;
(2)若函数h(x)=f (x)-g(x)在[1,4]上单调递减,求a的取值范围.
解:(1)h(x)=ln x-eq \f(1,2)ax2-2x,x∈(0,+∞),
所以h′(x)=eq \f(1,x)-ax-2.
因为h(x)在(0,+∞)上存在单调递减区间,
所以当x∈(0,+∞)时,eq \f(1,x)-ax-2<0有解,即a>eq \f(1,x2)-eq \f(2,x)有解.
设G(x)=eq \f(1,x2)-eq \f(2,x),所以只要a>G(x)min即可.
而G(x)=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)-1)) eq \s\up4(2)-1,
所以G(x)min=-1,所以a>-1.
又因为a≠0,所以a的取值范围为(-1,0)∪(0,+∞).
(2)因为h(x)在[1,4]上单调递减,
所以当x∈[1,4]时,h′(x)=eq \f(1,x)-ax-2≤0恒成立,即a≥eq \f(1,x2)-eq \f(2,x)恒成立.
由(1)知G(x)=eq \f(1,x2)-eq \f(2,x),
所以a≥G(x)max.
而G(x)=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)-1)) eq \s\up4(2)-1.
因为x∈[1,4],所以eq \f(1,x)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,4),1)),所以G(x)max=-eq \f(7,16)(此时x=4),所以a≥-eq \f(7,16).
又因为a≠0,所以a的取值范围是eq \b\lc\[\rc\)(\a\vs4\al\c1(-\f(7,16),0))∪(0,+∞).
本例第(2)问中,若h(x)在[1,4]上存在单调递减区间,求a的取值范围.
解:若h(x)在[1,4]上存在单调递减区间,
则h′(x)<0在[1,4]上有解,
所以当x∈[1,4]时,a>eq \f(1,x2)-eq \f(2,x)有解.
又当x∈[1,4]时,eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x2)-\f(2,x)))min=-1,
所以a>-1.
又因为a≠0,所以a的取值范围是(-1,0)∪(0,+∞).
根据函数的单调性求参数的一般思路
(1)利用集合间的包含关系处理:y=f (x)在区间(a,b)上单调,则区间(a,b)是相应单调区间的子集.
(2)f (x)单调递增的充要条件是对任意的x∈(a,b)都有f ′(x)≥0且在(a,b)内的任一非空子区间上,f ′(x)不恒为零,要注意等号是否可以取到.
(3)注意区分“在区间上恒成立”与“在区间上存在x值使不等式成立”的区别.分离参数后对应不同的最值类型.
1.已知定义域为R的奇函数y=f (x)的导函数为y=f ′(x).当x>0时,xf ′(x)-f (x)
相关教案
这是一份新高考数学一轮复习讲练教案3.2 第1课时 导数与函数的单调性、极值与最值(含解析),共6页。
这是一份高考数学一轮复习教案 第2章_第11节_导数与函数的单调性(含答案解析),共10页。
这是一份第3章 第2节 第4课时 利用导数研究不等式恒成立问题-2022届高三数学一轮复习讲义(新高考)教案,共14页。