2020-2021学年北京十二中七年级（下）开学数学试卷

这是一份2020-2021学年北京十二中七年级（下）开学数学试卷，共24页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
1．（3分）规定：（→3）表示向右移动3，记作+3，则（←2），记作（ ）
A．+2B．﹣2C．+D．﹣
2．（3分）截止到6月12日14时，美国新冠病毒确诊感染人数累计约209万人，死亡人数累计约为1.16×105人．下列用科学记数法表示感染人数和用原数表示死亡人数正确的是（ ）
A．2.09×106和11600B．2.09×106和116000
C．20.9×105和116000D．2.09×107和11600
3．（3分）如图所示，这个圆锥的侧面展开图可能是（ ）
A．B．
C．D．
4．（3分）下列各式中运算正确的是（ ）
A．3a2b﹣4ba2＝﹣a2bB．a2+a2＝a4
C．6a﹣5a＝1D．3a2+2a3＝5a5
5．（3分）已知有理数a，b，c在数轴上的位置如图，则下列结论错误的是（ ）
A．c﹣a＜0B．b+c＜0C．a+b﹣c＜0D．|a+b|＝a+b
6．（3分）已知关于x的一元一次方程2（x﹣1）+3a＝3的解为x＝4，则a的值是（ ）
A．﹣1B．1C．﹣2D．﹣3
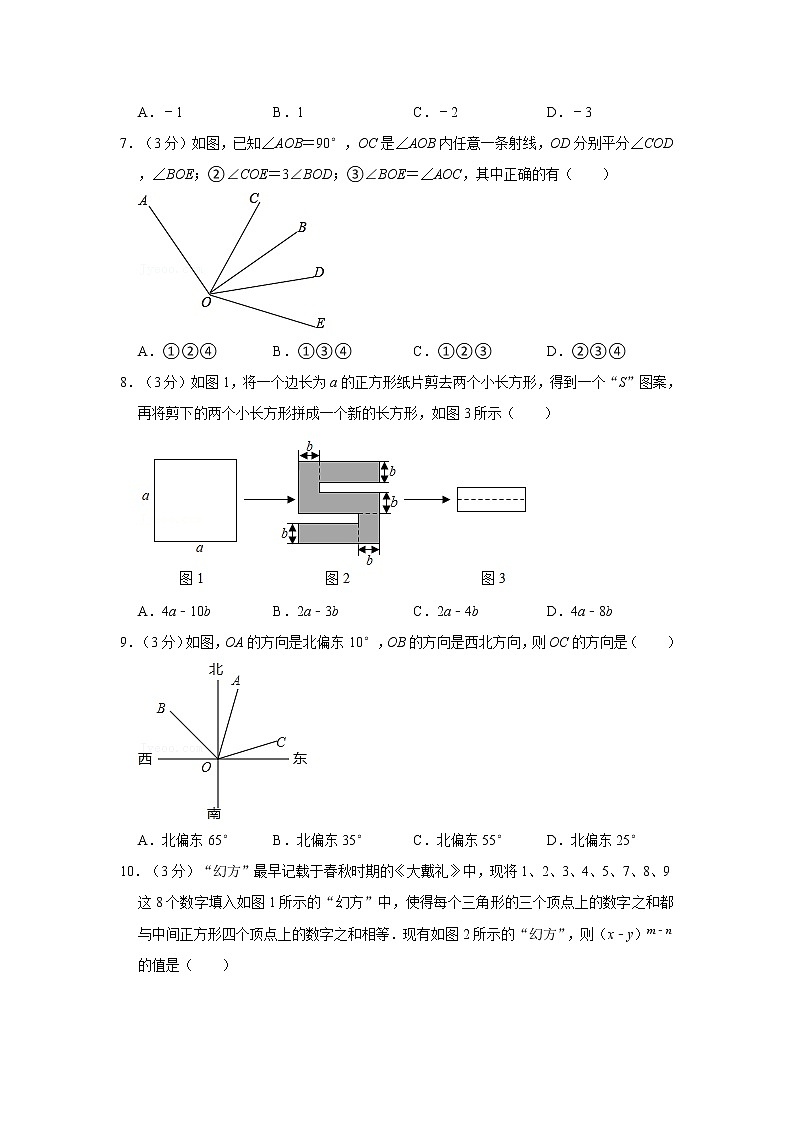
7．（3分）如图，已知∠AOB＝90°，OC是∠AOB内任意一条射线，OD分别平分∠COD，∠BOE；②∠COE＝3∠BOD；③∠BOE＝∠AOC，其中正确的有（ ）
A．①②④B．①③④C．①②③D．②③④
8．（3分）如图1，将一个边长为a的正方形纸片剪去两个小长方形，得到一个“S”图案，再将剪下的两个小长方形拼成一个新的长方形，如图3所示（ ）
A．4a﹣10bB．2a﹣3bC．2a﹣4bD．4a﹣8b
9．（3分）如图，OA的方向是北偏东10°，OB的方向是西北方向，则OC的方向是（ ）
A．北偏东65°B．北偏东35°C．北偏东55°D．北偏东25°
10．（3分）“幻方”最早记载于春秋时期的《大戴礼》中，现将1、2、3、4、5、7、8、9这8个数字填入如图1所示的“幻方”中，使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等．现有如图2所示的“幻方”，则（x﹣y）m﹣n的值是（ ）
A．﹣27B．﹣1C．8D．16
二、填空题（本大题共8小题，每小题2分，共16分）
11．（2分）比较大小：﹣（+2） ﹣|﹣3|（填＞，＜，＝）
12．（2分）单项式的次数是 ，系数是 ．
13．（2分）已知∠α与∠β互为余角，∠α＝38°24'，则∠β＝ ．
14．（2分）我国元朝朱世杰所著的《算学启蒙》（1299年）一书，有一道题目是：“今有良马日行二百四十里，问良马几何日追及之．”译文是：“跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，设快马x天可以追上慢马，则可以列方程为 ．
15．（2分）已知∠AOB＝60°，∠BOC＝40°，OE平分∠AOB，则∠EOF的度数为 ．
16．（2分）已知数a，b，c的大小关系如图所示：
则下列各式：
①b+a+（﹣c）＞0；②（﹣a）﹣b+c＞0；③；⑤|a﹣b|﹣|c+b|+|a﹣c|＝﹣2b．其中正确的有 （请填写编号）．
17．（2分）某公园划船项目收费标准如下：
某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为 元．
18．（2分）如图，是一个运算程序的示意图，若开始输入x的值为625 ．
三、解答题（本大题共10小题，共54分）
19．计算：
（1）（﹣20）+（+3）﹣（﹣5）﹣（+7）．
（2）（﹣+）÷﹣（﹣1）2021．
20．解方程：
（1）2（x﹣3）＝﹣3（x﹣1）+2．
（2）＝3﹣．
21．先化简，再求值．3（a2b﹣ab2）﹣2（a2b﹣1）﹣2ab2﹣2，其中，a＝﹣2
22．如图，已知三点A、B、C，请用尺规作图完成．（保留作图痕迹，不要求写作法）
（1）画直线AB；
（2）画射线AC；
（3）连接BC并延长BC到E，使得CE＝AB+AC．
23．某区中学生足球联赛共赛8轮（即每队均需赛8场），胜一场得3分，平一场得1分，小平安队踢平的场数是所负场数的2倍，共得17分
24．如图，∠AOB＝90°，∠COD＝90°，若∠1＝30°，求∠COE的度数．
解：∵∠AOB＝90°
∴∠1与∠2互余
∵∠COD＝90°
∴∠BOC与∠2互余
∴∠1＝∠ （ ）
∵∠1＝30°
∴∠BOC＝30°
∵OE平分∠BOC（已知）
∴∠COE＝BOC
∴∠COE＝15°
25．致敬，最美逆行者!
病毒虽无情，人间有大爱，2020年，全国（除湖北省外）共有30个省（区、市），白衣执甲，前赴后继支援湖北省抗击疫情（区、市）累计派出医务人员总数多达38478人，其中派往湖北省除武汉外的其他地区的医务人员总数为7381人．
a．全国30个省（区、市）各派出支援武汉的医务人员频数分布直方图（数据分成6组）如图；
b．全国30个省（区、市）各派出支援武汉的医务人员人数在900≤x＜1300这一组的是：919，997，1068，1101，1179，1194，1262．
根据以上信息回答问题：
（1）这次支援湖北省抗疫中，全国30个省（区、市）派往武汉的医务人员总数 ．
A．不到3万人
B．在3万人到3.5万人之间
C．超过3.5万人
（2）全国30个省（区、市）各派出支援武汉，其中医务人员人数超过1000人的省共有 个．
（3）据新华网报道，在支援湖北省的医务人员大军中，有“90后”也有“00后”，时代的脊梁．小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据：
C市派出的1514名医护人员中有414人是“90后”；
H市派出的338名医护人员中有103人是“90后”；
B市某医院派出的148名医护人员中有83人是“90后”；
小华还了解到除全国30个省（区、市）派出38478名医务人员外，军队派出了近四千名医务人员（按4.2万人计）中，“90后”大约有多少万人？
26．我们规定；若关于x的一元一次方程a+x＝b（a≠0）的解为x＝，则方程2+x＝4是“商解方程”．请回答下列问题：
（1）判断4+x＝是不是“商解方程”，并说明理由．
（2）若关于x的一元一次方程6+x＝m+3是“商解方程”，求m的值．
27．如图，点O是直线AB上的一点，将一直角三角板如图摆放
（1）如图1，如果∠AOC＝40°，依题意补全图形（不必写出完整的推理过程）；
（2）当直角三角板绕点O顺时针旋转一定的角度得到图2，使得直角边OC在直线AB的上方，若∠AOC＝α，请你直接用含α的代数式表示∠DOE的度数；
（3）当直角三角板绕点O继续顺时针旋转一周，回到图1的位置，在旋转过程中你发现∠AOC与∠DOE（0°≤∠AOC≤180°，0°≤∠DOE≤180°）
28．如图，线段AB＝15厘米，P是AB上任一点，且C点的运动速度为3厘米/秒，D点的运动速度为2厘米/秒
（1）若BP＝10厘米．
①运动1秒时，CP＝ 厘米，DB＝ 厘米，CD＝ 厘米；
②当C在线段AP上运动时，试说明BD＝2CD；
（2）如果运动3秒时，CD＝2厘米，试探索PB的值．
2020-2021学年北京十二中七年级（下）开学数学试卷
参考答案与试题解析
一、选择题本大题共10小题，每小题3分，共30分）
1．（3分）规定：（→3）表示向右移动3，记作+3，则（←2），记作（ ）
A．+2B．﹣2C．+D．﹣
【分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．“正”和“负”相对，所以（←2）表示向左移动2记作﹣2．
【解答】解：（←2）表示向左移动2，记作﹣3．
故选：B．
2．（3分）截止到6月12日14时，美国新冠病毒确诊感染人数累计约209万人，死亡人数累计约为1.16×105人．下列用科学记数法表示感染人数和用原数表示死亡人数正确的是（ ）
A．2.09×106和11600B．2.09×106和116000
C．20.9×105和116000D．2.09×107和11600
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．
【解答】解：209万＝209×10000＝2.09×106，
用原数表示死亡人数：4.16×105＝116000．
故选：B．
3．（3分）如图所示，这个圆锥的侧面展开图可能是（ ）
A．B．
C．D．
【分析】根据圆锥的侧面展开图是扇形，结合选项即可求解．
【解答】解：观察图形可知，这个圆锥的侧面展开图可能是．
故选：B．
4．（3分）下列各式中运算正确的是（ ）
A．3a2b﹣4ba2＝﹣a2bB．a2+a2＝a4
C．6a﹣5a＝1D．3a2+2a3＝5a5
【分析】合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变，据此判断即可．
【解答】解：A、3a2b﹣8ba2＝﹣a2b，故本选项符合题意；
B、a4+a2＝2a4，故本选项不符合题意；
C、6a﹣5a＝a；
D、4a2与2a4不是同类项，所以不能合并；
故选：A．
5．（3分）已知有理数a，b，c在数轴上的位置如图，则下列结论错误的是（ ）
A．c﹣a＜0B．b+c＜0C．a+b﹣c＜0D．|a+b|＝a+b
【分析】根据数轴比较实数a、b、c，a＞0，b＜0，c＜0，﹣c＞a＝﹣b，即可分析得出答案．
【解答】解：A、∵c＜0，
∴c﹣a＜0，故此选项正确；
B、∵b＜4，
∴b+c＜0，故此选项正确；
C、∵﹣c＞a＝﹣b，
∴a+b＝0，
∴a+b﹣c＞5，故此选项错误；
D、∵a＝﹣b，
∴|a+b|＝a+b，故此选项正确．
故选：C．
6．（3分）已知关于x的一元一次方程2（x﹣1）+3a＝3的解为x＝4，则a的值是（ ）
A．﹣1B．1C．﹣2D．﹣3
【分析】将x＝4代入方程中即可求出a的值．
【解答】解：将x＝4代入2（x﹣5）+3a＝3，
∴7×3+3a＝5，
∴a＝﹣1，
故选：A．
7．（3分）如图，已知∠AOB＝90°，OC是∠AOB内任意一条射线，OD分别平分∠COD，∠BOE；②∠COE＝3∠BOD；③∠BOE＝∠AOC，其中正确的有（ ）
A．①②④B．①③④C．①②③D．②③④
【分析】根据角平分线的意义，互余的意义和等量代换，逐个结论进行判断即可得出答案．
【解答】解：∵OB，OD分别平分∠COD，
∴∠COB＝∠BOD＝∠DOE，
∴∠COB+∠BOD＝∠BOD+∠DOE，
即：∠COD＝∠BOE，因此①正确；
∠COE＝∠COD+∠BOD+∠DOE＝3∠BOD，因此②正确；
∵∠AOB＝90°，
∴∠AOC+∠BOC＝90°＝∠AOC+∠BOD，因此④正确；
∵∠AOC≠2∠BOC＝∠BOE，因此③不正确；
故选：A．
8．（3分）如图1，将一个边长为a的正方形纸片剪去两个小长方形，得到一个“S”图案，再将剪下的两个小长方形拼成一个新的长方形，如图3所示（ ）
A．4a﹣10bB．2a﹣3bC．2a﹣4bD．4a﹣8b
【分析】根据题意找出新长方形的长与宽，进而表示出周长即可．
【解答】解：根据题意得：新长方形的长为a﹣b，宽为a﹣3b，
则新长方形的周长为2[（a﹣b）+（a﹣7b）]＝2（2a﹣4b）＝4a﹣8b．
故选：D．
9．（3分）如图，OA的方向是北偏东10°，OB的方向是西北方向，则OC的方向是（ ）
A．北偏东65°B．北偏东35°C．北偏东55°D．北偏东25°
【分析】首先求得∠AOB的度数，然后求得OC与正北方向的夹角即可判断．
【解答】解：∠AOB＝45°+10°＝55°，
则∠AOC＝∠AOB＝55°，OC与正北方向的夹角是55+10＝65°．
则OC在北偏东65°．
故选：A．
10．（3分）“幻方”最早记载于春秋时期的《大戴礼》中，现将1、2、3、4、5、7、8、9这8个数字填入如图1所示的“幻方”中，使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等．现有如图2所示的“幻方”，则（x﹣y）m﹣n的值是（ ）
A．﹣27B．﹣1C．8D．16
【分析】根据：每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，可得：x+2＝y+（﹣1），m+（﹣1）＝n+2，据此分别求出x﹣y，m﹣n的值各是多少，即可求出（x﹣y）m﹣n的值是多少．
【解答】解：根据题意，可得：
x+2＝y+（﹣1），m+（﹣2）＝n+2，
∴x﹣y＝﹣3，m﹣n＝7，
∴（x﹣y）m﹣n
＝（﹣3）3
＝﹣27
故选：A．
二、填空题（本大题共8小题，每小题2分，共16分）
11．（2分）比较大小：﹣（+2） ＞ ﹣|﹣3|（填＞，＜，＝）
【分析】根据两个负数比较大小，其绝对值大的反而小比较即可．
【解答】解：∵﹣（+2）＝﹣2，﹣|﹣8|＝﹣3，
∴﹣（+2）＞﹣|﹣7|．
故答案为：＞
12．（2分）单项式的次数是 5 ，系数是 ﹣ ．
【分析】根据单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数可得答案．
【解答】解：单项式的次数是5，
故答案为：5；﹣．
13．（2分）已知∠α与∠β互为余角，∠α＝38°24'，则∠β＝ 51°36′（或51.6°） ．
【分析】互为余角的两角和为90°，计算可得．
【解答】解：∵∠α与∠β互为余角，∠α＝38°24'，
∴∠β＝90°﹣38°24'＝51°36′（或51.6°）．
故答案为：51°36′（或51.6°）．
14．（2分）我国元朝朱世杰所著的《算学启蒙》（1299年）一书，有一道题目是：“今有良马日行二百四十里，问良马几何日追及之．”译文是：“跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，设快马x天可以追上慢马，则可以列方程为 240x﹣150x＝150×12 ．
【分析】设快马x天可以追上慢马，根据慢马先行的路程＝快慢马速度之差×快马行走天数，即可列出关于x的一元一次方程，解之即可得出结论．
【解答】解：设快马x天可以追上慢马，
由题意，得240x﹣150x＝150×12．
故答案是：240x﹣150x＝150×12．
15．（2分）已知∠AOB＝60°，∠BOC＝40°，OE平分∠AOB，则∠EOF的度数为 20° ．
【分析】分两种情况：当OC在∠AOB的内部时，当OC在∠AOB的外部时，根据角平分线的性质计算出∠AOE，∠AOF的度数，然后根据角的和差关系即可算出∠EOF的度数．
【解答】解：如图1，当OC在∠AOB的内部时，
∵∠AOB＝60，∠BOC＝40°，
∴∠AOC＝20°，
∵OE平分∠AOB，OF平分∠AOC，
∴∠AOE＝∠BOE＝∠AOB＝30°∠AOC＝10°，
∴∠EOF＝30°﹣10°＝20°．
如图7，当OC在∠AOB的外部时，
∵∠AOB＝60，∠BOC＝40°，
∴∠AOC＝100°，
∵OE平分∠AOB，OF平分∠AOC，
∴∠AOE＝∠BOE＝∠AOB＝30°∠AOC＝50°，
∴∠EOF＝50°﹣30°＝20°．
故答案为：20°．
16．（2分）已知数a，b，c的大小关系如图所示：
则下列各式：
①b+a+（﹣c）＞0；②（﹣a）﹣b+c＞0；③；⑤|a﹣b|﹣|c+b|+|a﹣c|＝﹣2b．其中正确的有 ②③⑤ （请填写编号）．
【分析】有数轴判断abc的符号和它们绝对值的大小，再判断所给出的式子的符号，写出正确的答案．
【解答】解：由数轴知b＜0＜a＜c，|a|＜|b|＜|c|，
①b+a+（﹣c）＜0，故原式错误；
②（﹣a）﹣b+c＞5，故正确；
③，故正确；
④bc﹣a＜0，故原式错误；
⑤|a﹣b|﹣|c+b|+|a﹣c|＝﹣4b，故正确；
其中正确的有②③⑤．
17．（2分）某公园划船项目收费标准如下：
某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为 380 元．
【分析】分情况，列表格计算，即可得出结论．
【解答】解：如图，由题意列表得，
所以，费用最少为380元，
故答案为：380．
18．（2分）如图，是一个运算程序的示意图，若开始输入x的值为625 1 ．
【分析】依次求出每次输出的结果，根据结果得出规律，即可得出答案．
【解答】解：当x＝625时，x＝125，
当x＝125时，x＝25，
当x＝25时，x＝5，
当x＝5时，x＝1，
当x＝4时，x+4＝5，
当x＝5时，x＝2，
…
依此类推，以5，
（2020﹣2）÷3＝1009，能够整除，
所以输出的结果是1，
故答案为：1
三、解答题（本大题共10小题，共54分）
19．计算：
（1）（﹣20）+（+3）﹣（﹣5）﹣（+7）．
（2）（﹣+）÷﹣（﹣1）2021．
【分析】（1）根据有理数的加减法可以解答本题；
（2）先把除法转化为乘法，然后根据乘法分配律即可解答本题．
【解答】解：（1）（﹣20）+（+3）﹣（﹣5）﹣（+7）
＝（﹣20）+3+5+（﹣6）
＝[（﹣20）+（﹣7）]+（3+7）
＝（﹣27）+8
＝﹣19；
（2）（﹣+）÷2021
＝（﹣+）×24﹣（﹣8）
＝×24﹣×24+1
＝16﹣18+21+1
＝20．
20．解方程：
（1）2（x﹣3）＝﹣3（x﹣1）+2．
（2）＝3﹣．
【分析】（1）（2）根据解一元一次方程的一般步骤解出方程．
【解答】解：（1）去括号，得2x﹣6＝﹣6x+3+2，
移项，得5x+3x＝3+2+6，
合并同类项，得5x＝11，
系数化为8，得x＝；
（2）去分母，得4（6﹣x）＝3×12﹣3（x+8），
去括号，得4﹣4x＝36﹣3x﹣6，
移项，得﹣4x+4x＝36﹣6﹣4，
合并同类项，得﹣x＝26，
系数化为4，得x＝﹣26．
21．先化简，再求值．3（a2b﹣ab2）﹣2（a2b﹣1）﹣2ab2﹣2，其中，a＝﹣2
【分析】先化简原式，再把a＝﹣2，b＝2代入求值即可．
【解答】解：原式＝3a2b﹣4ab2﹣2a3b+2﹣2ab6﹣2，
＝a2b﹣8ab2，
把a＝﹣2，b＝7代入
原式＝（﹣2）2×2﹣5×（﹣2）×52
＝8+40
＝48．
22．如图，已知三点A、B、C，请用尺规作图完成．（保留作图痕迹，不要求写作法）
（1）画直线AB；
（2）画射线AC；
（3）连接BC并延长BC到E，使得CE＝AB+AC．
【分析】根据直线，射线，线段的定义解决问题即可．
【解答】解：（1）如图，直线AB即为所求作．
（2）如图，射线AC即为所求作．
（3）如图，线段CE即为所求作．
23．某区中学生足球联赛共赛8轮（即每队均需赛8场），胜一场得3分，平一场得1分，小平安队踢平的场数是所负场数的2倍，共得17分
【分析】表示出该队胜，负，平的场数，等量关系为：胜的场数的得分+平的场数的得分＝17，把相关数值代入求解即可．
【解答】解：设负的场数为x，则平的场数为2x，
3（5﹣x﹣2x）+2x＝17，
解得x＝7，
∴8﹣x﹣2x＝7．
答：胜了5场．
24．如图，∠AOB＝90°，∠COD＝90°，若∠1＝30°，求∠COE的度数．
解：∵∠AOB＝90°
∴∠1与∠2互余 互余定义
∵∠COD＝90°
∴∠BOC与∠2互余
∴∠1＝∠ BOC （ 同角的余角相等 ）
∵∠1＝30°
∴∠BOC＝30° 等量代换
∵OE平分∠BOC（已知）
∴∠COE＝BOC 角平分线定义
∴∠COE＝15°
【分析】根据角度的计算，角平分线的定义解答即可．
【解答】解：∵∠AOB＝90°
∴∠1与∠2互余（互余定义）
∵∠COD＝90°
∴∠BOC与∠7互余
∴∠1＝∠BOC （ 同角的余角相等）
∵∠1＝30°
∴∠BOC＝30° （等量代换）
∵OE平分∠BOC（已知）
∴∠COE＝BOC （角平分线定义）
∴∠COE＝15°；
故答案为：互余定义；BOC；等量代换．
25．致敬，最美逆行者!
病毒虽无情，人间有大爱，2020年，全国（除湖北省外）共有30个省（区、市），白衣执甲，前赴后继支援湖北省抗击疫情（区、市）累计派出医务人员总数多达38478人，其中派往湖北省除武汉外的其他地区的医务人员总数为7381人．
a．全国30个省（区、市）各派出支援武汉的医务人员频数分布直方图（数据分成6组）如图；
b．全国30个省（区、市）各派出支援武汉的医务人员人数在900≤x＜1300这一组的是：919，997，1068，1101，1179，1194，1262．
根据以上信息回答问题：
（1）这次支援湖北省抗疫中，全国30个省（区、市）派往武汉的医务人员总数 ．
A．不到3万人
B．在3万人到3.5万人之间
C．超过3.5万人
（2）全国30个省（区、市）各派出支援武汉，其中医务人员人数超过1000人的省共有 15 个．
（3）据新华网报道，在支援湖北省的医务人员大军中，有“90后”也有“00后”，时代的脊梁．小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据：
C市派出的1514名医护人员中有414人是“90后”；
H市派出的338名医护人员中有103人是“90后”；
B市某医院派出的148名医护人员中有83人是“90后”；
小华还了解到除全国30个省（区、市）派出38478名医务人员外，军队派出了近四千名医务人员（按4.2万人计）中，“90后”大约有多少万人？
【分析】（1）支援全省的人数减去支援武汉的人数即可；
（2）根据频数分布直方图和所列举的数据可得答案；
（3）求出样本中“90后”所占的百分比即可求出相应的人数．
【解答】解：（1）38487﹣7381＝31097（人），
因此选B，
故答案为：B；
（2）从频数分布直方图可知，人数在900名及以上的有10+4+2+6＝17个省，
列举的人数在900≤x＜1300的有两个省人数吧超过1000人，
因此10+4+2+5﹣2＝15（个），
故答案为：15；
（3）4.8×＝4.2×，
答：在支援湖北省的全体医务人员（按3.2万人计）中，“90后”大约有1.26万人．
26．我们规定；若关于x的一元一次方程a+x＝b（a≠0）的解为x＝，则方程2+x＝4是“商解方程”．请回答下列问题：
（1）判断4+x＝是不是“商解方程”，并说明理由．
（2）若关于x的一元一次方程6+x＝m+3是“商解方程”，求m的值．
【分析】（1）先解出方程，再求出，根据“商解方程”的定义证明；
（2）根据“商解方程”的定义解答即可．
【解答】解：（1）4+x＝是“商解方程”，
理由如下：方程8+x＝的解为：x＝，
∵÷4＝，
∴4+x＝是“商解方程”；
（2）6+x＝m+3，
x＝m﹣6，
∵一元一次方程6+x＝m+3是“商解方程”，
∴m﹣6＝，
解得，m＝．
27．如图，点O是直线AB上的一点，将一直角三角板如图摆放
（1）如图1，如果∠AOC＝40°，依题意补全图形（不必写出完整的推理过程）；
（2）当直角三角板绕点O顺时针旋转一定的角度得到图2，使得直角边OC在直线AB的上方，若∠AOC＝α，请你直接用含α的代数式表示∠DOE的度数；
（3）当直角三角板绕点O继续顺时针旋转一周，回到图1的位置，在旋转过程中你发现∠AOC与∠DOE（0°≤∠AOC≤180°，0°≤∠DOE≤180°）
【分析】（1）根据角平分线的作法作出OE平分∠BOC，先根据平角的定义求出∠BOC，再根据角平分线的定义求出∠COE，再根据直角的定义即可求解；
（2）先根据平角的定义求出∠BOC，再根据角平分线的定义求出∠COE，再根据直角的定义即可求解；
（3）分两种情况：0°≤∠AOC≤180°，0°≤∠DOE≤180°，可求∠AOC与∠DOE之间的数量关系．
【解答】解：（1）如图1，补全图形；
解题思路如下：
①由∠AOC+∠BOC＝180°，∠AOC＝40°，
得∠BOC＝140°；
②由OE平分∠BOC，
得∠COE＝70°；
③由直角三角板，
得∠COD＝90°；
④由∠COD＝90°，∠COE＝70°，
得∠DOE＝20°．
（2）①由∠AOC+∠BOC＝180°，∠AOC＝α，
得∠BOC＝180°﹣α；
②由OE平分∠BOC，
得∠COE＝90°﹣α；
③由直角三角板，
得∠COD＝90°；
④由∠COD＝90°，∠COE＝90°﹣α，
得∠DOE＝． 
（3）∠DOE＝∠AOC（3°≤∠AOC≤180°）∠AOC（8°≤∠DOE≤180°）．
28．如图，线段AB＝15厘米，P是AB上任一点，且C点的运动速度为3厘米/秒，D点的运动速度为2厘米/秒
（1）若BP＝10厘米．
①运动1秒时，CP＝ 2 厘米，DB＝ 8 厘米，CD＝ 4 厘米；
②当C在线段AP上运动时，试说明BD＝2CD；
（2）如果运动3秒时，CD＝2厘米，试探索PB的值．
【分析】（1）①先求出PB、CP与DB的长度，然后利用CD＝CP+PB﹣DB即可求出答案；
②用t表示出AC、DP、BD、CD的长度即可求证BD＝2CD；
（2）当t＝3时，求出DB的长度，由于没有说明D点在C点的左边还是右边，故需要分情况讨论．
【解答】解：（1）①CP＝15﹣10﹣3＝2（厘米），DB＝10﹣4＝8（厘米）．
故答案为：2，7，4；
②由题意可得：AC＝3t，DP＝8t，BP＝10，
∴BD＝10﹣2t，CB＝15﹣3t，
∴CD＝CB﹣DB＝15﹣4t﹣（10﹣2t）＝5﹣t，
∴BD＝8CD；
（2）设PB＝x，则AP＝15﹣x，
由题意可得：AC＝9，PD＝6，
∴DB＝PB﹣PD＝x﹣6，
①当点C在点D的左边时，
∵CD＝AB﹣AC﹣DB＝15﹣9﹣（x﹣6），CD＝2，
∴15﹣9﹣（x﹣6）＝2，
解得x＝10；
②当点C在点D的右边时，
∵CD＝AC﹣AP﹣DP＝9﹣（15﹣x）﹣6，CD＝8，
∴9﹣（15﹣x）﹣6＝8，
解得x＝14．
综上所述，PB的值是10或14．
船型
两人船（限乘两人）
四人船（限乘四人）
六人船（限乘六人）
八人船（限乘八人）
每船租金（元/小时）
90
100
130
150
船型
两人船（限乘两人）
四人船（限乘四人）
六人船（限乘六人）
八人船（限乘八人）
每船租金（元/小时）
90
100
130
150