

2020-2021学年江苏省南京市栖霞区九年级(下)开学数学试卷
展开2020-2021学年江苏省南京市栖霞区九年级(下)开学数学试卷
一、选择题(本大题共6小题,每小题2分,共12分)
1.(2分)3的平方根是( )
A.9 B. C.﹣ D.±
2.(2分)下列运算结果正确的是( )
A.a2+a3=a5 B.a2•a3=a6 C.a3÷a2=a D.(a2)3=a5
3.(2分)某校运动会中,九年级有13名女同学参加女子百米竞赛,预赛成绩各不相同,小梅已经知道了自己的成绩,她想知道自己能否进入决赛( )
A.平均数 B.众数 C.中位数 D.方差
4.(2分)如图,BD为⊙O的直径,点A、C在⊙O上,则∠CBD的度数为( )
A.40° B.45° C.50° D.60°
5.(2分)如图,D、E分别为△ABC的边AB、AC上的点,且DE∥BC,BD=2AD.若△ODE的面积为1,则△BCE的面积为( )
A.6 B.8 C.10 D.12
6.(2分)如图,二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象与x轴的一个交点坐标为(﹣1,0),对称轴为直线x=1.下列结论:①x>0时;②2a+b=0;③4a+2b+c<02+bx+c+a=0有两个不相等的实数根.其中,所有正确结论的序号为( )
A.②③ B.②④ C.①②③ D.②③④
二、填空题(本大题共10小题,每小题2分,共20分)
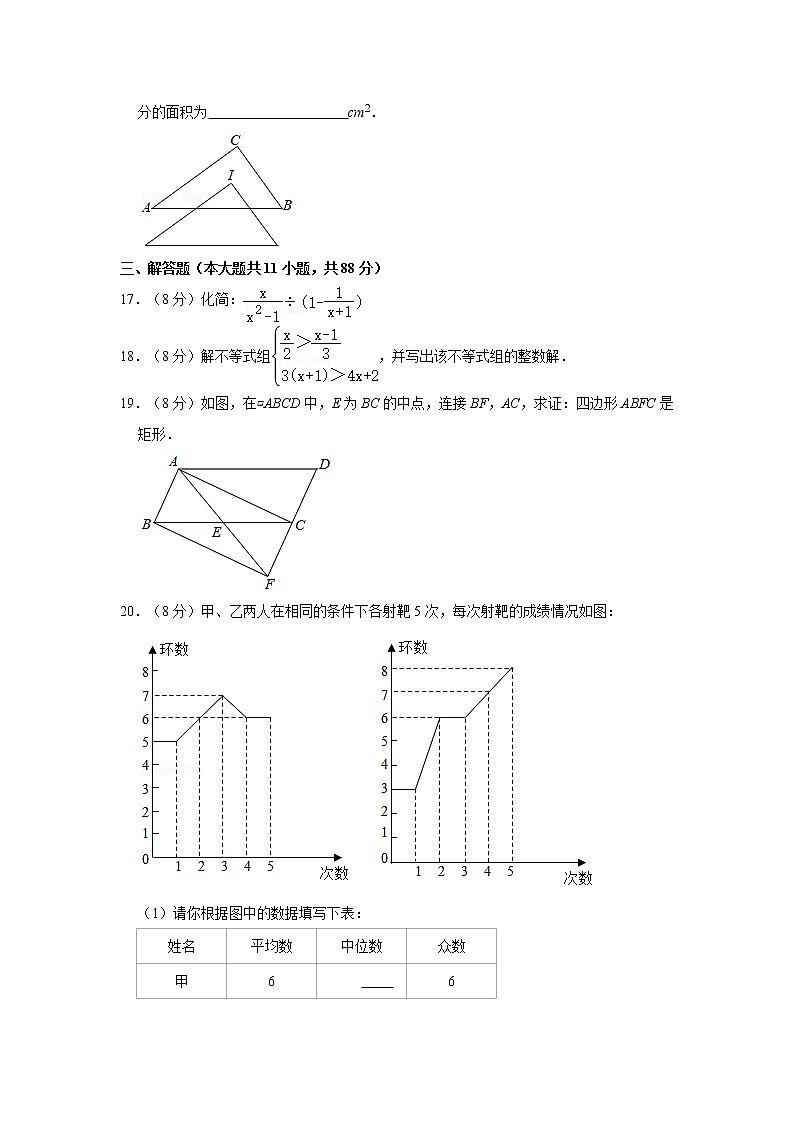
7.(2分)南京在建的地铁6号线由栖霞山站开往南京南站,全长32400米.用科学记数法表示32400是 .
8.(2分)要使在实数范围内有意义,x的取值范围是 .
9.(2分)分解因式:(a+b)2﹣4ab= .
10.(2分)计算﹣的结果是 .
11.(2分)已知圆锥的底面半径为1cm,母线长为3cm,则其侧面积为 cm2.(结果保留π)
12.(2分)若x1、x2是一元二次方程x2﹣4x+3=0的两个实数根,则x1+x2﹣x1x2= .
13.(2分)将二次函数y=x2+1的图象向右平移1个单位后再沿x轴翻折,得到的图象对应的函数表达式是 .
14.(2分)在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q(0,2),N(0,8),则点P的坐标为 .
15.(2分)如图,点A、B、C、D在⊙O上,B是,过C作⊙O的切线交AB的延长线于点E.若∠AEC=84°,则∠ADC= °.
16.(2分)如图,点I为△ABC的内心,AB=5cm,BC=3cm,将△ABC平移,则重叠部分的面积为 cm2.
三、解答题(本大题共11小题,共88分)
17.(8分)化简:
18.(8分)解不等式组,并写出该不等式组的整数解.
19.(8分)如图,在▱ABCD中,E为BC的中点,连接BF,AC,求证:四边形ABFC是矩形.
20.(8分)甲、乙两人在相同的条件下各射靶5次,每次射靶的成绩情况如图:
(1)请你根据图中的数据填写下表:
姓名
平均数
中位数
众数
甲
6
6
乙
6
(2)利用方差判断这5次射靶是甲的成绩波动大还是乙的成绩波动大.
21.(8分)某校计划在暑假第二周的星期一至星期四开展社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择两天,其中有一天是星期二的概率是多少?
(2)乙同学随机选择连续的两天,其中有一天是星期二的概率是 .
22.(8分)为了提升小区形象,改善业主居住环境,开发商准备对小区进行绿化.利用长度为64m的篱笆和一段小区围墙搭建如图所示的矩形花圃(接口忽略不计),分别用来种植不同的花卉.则花圃的一边AB为多长时,花圃的面积为192m2.
23.(8分)如图,在▱ABCD中,过A、B、C三点的⊙O交AD于点E,BE=BC.
(1)求证:△BEC∽△CED;
(2)若BC=10,DE=3.6,求⊙O的半径.
24.(8分)快、慢两车分别从相距120千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,立即按原路返回,返回时的速度是去时速度的2倍1(千米)与出发后所用的时间x(小时)的关系如图所示.
请结合图象信息解答下列问题:
(1)慢车的速度是 千米/小时,快车的返回时速度是 千米/小时;
(2)画出快车距出发地的路程y2(千米)与出发后所用的时间x(小时)的函数图象;
(3)在快车返回途中,快、慢两车相距的路程为50千米时,慢车行驶了多少小时?
25.(8分)一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为 件.
(2)当每件商品降价多少元时,该商店每天销售利润最大,最大利润是多少元?
26.(8分)已知二次函数y=a(x﹣m)(x﹣m﹣6)(a、m为常数,且a≠0),该函数图象顶点A的纵坐标为﹣9.
(1)求证:该函数的图象与x轴有两个公共点.
(2)若该函数图象与y轴交于点B(0,﹣5),求该函数的表达式.
(3)若该函数图象过点(﹣6,y1)与(2,y2),比较y1、y2的大小.
27.(8分)如图,在△ABC中,AB=BC,过点C作∠ACD=∠ACB,且交⊙O于点D.连接BD交AC于点E,使得CF=CB,连接BF.
(1)求证:ED=EC.
(2)求证:BF是⊙O的切线.
(3)若点G为△BCD的内心,AE•AC=10.
①利用无刻度的直尺在图中画出点G的位置.(保留作图痕迹,不写作法)
②求AG的长.
2020-2021学年江苏省南京市栖霞区九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(本大题共6小题,每小题2分,共12分)
1.(2分)3的平方根是( )
A.9 B. C.﹣ D.±
【分析】如果一个数的平方等于a,那么这个数就叫做a的平方根,也叫做a的二次方根.一个正数有正、负两个平方根,它们互相为相反数;零的平方根是零,负数没有平方根.
【解答】解:∵()2=8,
∴3的平方根.
故选:D.
2.(2分)下列运算结果正确的是( )
A.a2+a3=a5 B.a2•a3=a6 C.a3÷a2=a D.(a2)3=a5
【分析】根据合并同类项法则,同底数幂相乘,底数不变指数相加;同底数幂相除,底数不变指数相减;幂的乘方,底数不变指数相乘对各选项分析判断即可得解.
【解答】解:A、a2与a3是加,不是乘,故本选项错误;
B、a5•a3=a2+5=a5,故本选项错误;
C、a3÷a8=a3﹣2=a,故本选项正确;
D、(a7)3=a2×8=a6,故本选项错误.
故选:C.
3.(2分)某校运动会中,九年级有13名女同学参加女子百米竞赛,预赛成绩各不相同,小梅已经知道了自己的成绩,她想知道自己能否进入决赛( )
A.平均数 B.众数 C.中位数 D.方差
【分析】由于有13名同学参加百米竞赛,要取前6名参加决赛,故应考虑中位数的大小.
【解答】解:共有13名学生参加竞赛,取前6名.我们把所有同学的成绩按大小顺序排列,所以小梅知道这组数据的中位数.
故选:C.
4.(2分)如图,BD为⊙O的直径,点A、C在⊙O上,则∠CBD的度数为( )
A.40° B.45° C.50° D.60°
【分析】根据同弧或等弧所对的圆周角相等得到∠BDC=∠A=40°,由BD为⊙O的直径,根据圆周角定理的推论:直径所对的圆周角为直角得到∠BCD=90°,然后利用三角形内角定理即可计算出∠CBD的度数.
【解答】解:∵∠A=40°,
∴∠BDC=40°,
又∵BD为⊙O的直径,
∴∠BCD=90°,
∴∠CBD=90°﹣40°=50°.
故选:C.
5.(2分)如图,D、E分别为△ABC的边AB、AC上的点,且DE∥BC,BD=2AD.若△ODE的面积为1,则△BCE的面积为( )
A.6 B.8 C.10 D.12
【分析】结合图形根据线段之间的和差关系可得到=,根据DE∥BC,推出△ADE∽ABC,△ODE∽OCB,从而根据相似三角形的性质推出==,从而推出=()2=,=,结合图形进行求解即可.
【解答】解:∵BD=2AD,AD+BD=AB,
∴=,
∵DE∥BC,
∴△ADE∽ABC,
∴==,
∵DE∥BC,
∴△ODE∽OCB,
∴==,
∴=()2=,=,
∵S△ODE=1,
∴S△OCB=9,S△OCE=2,
∴S△BCE=S△OCB+S△OCE=12,
故选:D.
6.(2分)如图,二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象与x轴的一个交点坐标为(﹣1,0),对称轴为直线x=1.下列结论:①x>0时;②2a+b=0;③4a+2b+c<02+bx+c+a=0有两个不相等的实数根.其中,所有正确结论的序号为( )
A.②③ B.②④ C.①②③ D.②③④
【分析】根据二次函数的图象及性质即可判断.
【解答】解:由函数图象可知,抛物线开口向上,
∴a>0,
∵对称轴为直线x=1,与轴的一个交点坐标为(﹣4,
∴与轴另一个交点坐标为(3,0),
∴当x>5时,y随x的增大而增大;
∵﹣=1,
∴b=﹣8a,
∴2a+b=0,故②正确;
当x=7时,y=4a+2b+c<6;
当x=﹣1时,y=a﹣b+c=3a+c=3,
∴c=﹣3a,
∴﹣a>c,
∴直线y=﹣a与抛物线y=ax2+x+c有5个交点,
∴关于x的方程ax2+bx+c=﹣a有两个不相等的实数根,
即关于a的方程ax2+bx+c+a=2有两个不相等的实数根,故④正确;
正确的有②③④,
故选:D.
二、填空题(本大题共10小题,每小题2分,共20分)
7.(2分)南京在建的地铁6号线由栖霞山站开往南京南站,全长32400米.用科学记数法表示32400是 3.24×104 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:用科学记数法表示32400是3.24×104.
故答案为:6.24×104.
8.(2分)要使在实数范围内有意义,x的取值范围是 x≠1 .
【分析】根据分母不为零分式有意义,可得答案.
【解答】解:由题意,得
1﹣x≠0,
解得x≠2,
故答案为:x≠1.
9.(2分)分解因式:(a+b)2﹣4ab= (a﹣b)2 .
【分析】首先利用完全平方公式去括号合并同类项,进而利用完全平方公式分解因式即可.
【解答】解:(a+b)2﹣4ab
=a2+2ab+b2﹣7ab
=a2+b2﹣6ab
=(a﹣b)2.
故答案为:(a﹣b)2.
10.(2分)计算﹣的结果是 .
【分析】先化简,再合并同类二次根式即可.
【解答】解:﹣
=2﹣
=.
故答案为:.
11.(2分)已知圆锥的底面半径为1cm,母线长为3cm,则其侧面积为 3π cm2.(结果保留π)
【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.
【解答】解:圆锥的侧面积=•3π•1•3=8π(cm2).
故答案为3π.
12.(2分)若x1、x2是一元二次方程x2﹣4x+3=0的两个实数根,则x1+x2﹣x1x2= 1 .
【分析】根据根与系数的关系得到x1+x2=4,x1x2=3,然后利用整体代入的方法计算.
【解答】解:根据题意得x1+x2=5,x1x2=4,
所以x1+x2﹣x8x2=(x1+x3)﹣x1x2=4﹣3=1.
故答案为7.
13.(2分)将二次函数y=x2+1的图象向右平移1个单位后再沿x轴翻折,得到的图象对应的函数表达式是 y=﹣x2+2x﹣2 .
【分析】根据“左加右减”的原则求得平移后的抛物线解析式,然后根据关于x轴对称的点的坐标特征即可求得沿x轴翻折后的函数表达式.
【解答】解:二次函数y=x2+1的图象向右平移6个单位得到新的函数解析式为y=(x﹣1)2+7,再将y=(x﹣1)2+8沿x轴翻折得到新的函数解析式为:y=﹣(x﹣1)2﹣7=﹣x2+2x﹣2,
故答案为:y=﹣x2+2x﹣3
14.(2分)在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q(0,2),N(0,8),则点P的坐标为 (4,5) .
【分析】根据已知条件,纵坐标易求;再根据切割线定理即OQ2=OM•ON求OQ可得横坐标.
【解答】解:过点P作PD⊥MN于D,连接PQ.
∵⊙P与x轴相切于点Q,与y轴交于M(0,N(0,
∴OM=5,NO=8,
∴NM=6,
∵PD⊥NM,
∴DM=6
∴OD=5,
∴OQ2=OM•ON=6×8=16,OQ=4.
∴PD=5,PQ=OD=3+2=8.
即点P的坐标是(4,5).
故答案是:(7,5).
15.(2分)如图,点A、B、C、D在⊙O上,B是,过C作⊙O的切线交AB的延长线于点E.若∠AEC=84°,则∠ADC= 64 °.
【分析】连接BD、BC,根据圆周角定理得出,根据圆内接四边形的性质得出∠EBC=∠ADC,根据切线的性质得出∠BCE=∠BDC=∠ADC,然后根据三角形内角和定理得出84°+∠ADC+∠ADC=180°,解得即可.
【解答】解:连接BD、BC,
∵B是的中点,
∴=,
∴,
∵四边形ABCD是圆内接四边形,
∴∠EBC=∠ADC,
∵EC是⊙O的切线,切点为C,
∴∠BCE=∠BDC=∠ADC,
∵∠AEC=84°,∠AEC+∠BCE+∠EBC=180°,
∴84°+∠ADC+∠ADC=180°,
∴∠ADC=64°.
故答案为64.
16.(2分)如图,点I为△ABC的内心,AB=5cm,BC=3cm,将△ABC平移,则重叠部分的面积为 cm2.
【分析】先由勾股你到了判断出三角形ABC为直角三角形,再根据内心得ID=IE=IH,再由等面积求出IH,CK,由平移性质知△ABC∽△GFI,即,再求出重叠部分的面积即可.
【解答】解:过点作ID⊥AC于点D,IE⊥BC于点E,连接IA,IC,
∵AB=5cm,AC=4cm,
∴AB6=25,AC2+BC2=52+38=25,
∴AB2=AC2+BC7,
∴△ABC为直角三角形,
∵I是△ABC的内心,
∴ID=IE=IH,
设ID=IE=IH=a,
则Rt△ABC的面积=AC•BC=,
解得:a=1,
如图,过C作CK⊥BC于K,
∵Rt△ABC的面积=AC•BC=,
解得:CK=cm,
∵将△ABC平移产生重叠部分△IGF,
∴AC∥GI,CB∥FI,
∴△ABC∽△GFI,
∴==,
∴=cm²,
∴重叠部分的面积为cm².
三、解答题(本大题共11小题,共88分)
17.(8分)化简:
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
【解答】解:原式=÷=•=.
18.(8分)解不等式组,并写出该不等式组的整数解.
【分析】此题可先根据一元一次不等式组解出x的取值,根据x是整数解得出x的可能取值.
【解答】解:,
解不等式①得,x>﹣2;
解不等式②得x<7,
∴不等式组的解集是:﹣2<x<1,
∴不等式组的整数解是:﹣5,0.
19.(8分)如图,在▱ABCD中,E为BC的中点,连接BF,AC,求证:四边形ABFC是矩形.
【分析】根据平行四边形的性质得到两角一边对应相等,利用AAS判定△ABE≌△FCE,从而得到AB=CF;由已知可得四边形ABFC是平行四边形,BC=AF,根据对角线相等的平行四边形是矩形,可得到四边形ABFC是矩形.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
20.(8分)甲、乙两人在相同的条件下各射靶5次,每次射靶的成绩情况如图:
(1)请你根据图中的数据填写下表:
姓名
平均数
中位数
众数
甲
6
6
6
乙
6
6
6
(2)利用方差判断这5次射靶是甲的成绩波动大还是乙的成绩波动大.
【分析】(1)从折线图上获取信息,根据平均数、中位数和众数的定义计算即可;
(2)利用方差公式计算求值即可.
【解答】解:(1)甲射靶的成绩为:5,6,8,6,7,
乙射靶的成绩为:4,6,6,6,8,
∴甲的中位数为:6,众数为:5,
乙的平均数为:=6,
故答案为:6,3,6;
(2)S甲2=[(6﹣2)2 +(6﹣6)2+(6﹣6)2+(6﹣6)2+(7﹣3)2]
=;
S乙2=[(3﹣6)4+(6﹣6)3+(6﹣6)6+(7﹣6)8+(8﹣6)5]
=.
因为S甲2<S乙7,
所以乙的成绩波动大.
21.(8分)某校计划在暑假第二周的星期一至星期四开展社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择两天,其中有一天是星期二的概率是多少?
(2)乙同学随机选择连续的两天,其中有一天是星期二的概率是 .
【分析】(1)由树状图得出共有12个等可能的结果,其中有一天是星期二的结果有6个,由概率公式即可得出结果;
(2)乙同学随机选择连续的两天,共有3个等可能的结果,即(星期一,星期二),(星期二,星期三),(星期三,星期四);其中有一天是星期二的结果有2个,由概率公式即可得出结果.
【解答】解:(1)画树状图如图所示:共有12个等可能的结果,其中有一天是星期二的结果有6个,
∴甲同学随机选择两天,其中有一天是星期二的概率为=;
(2)乙同学随机选择连续的两天,共有3个等可能的结果,星期二),星期三),星期四);
其中有一天是星期二的结果有8个,即(星期一,(星期二,
∴乙同学随机选择连续的两天,其中有一天是星期二的概率是;
故答案为:.
22.(8分)为了提升小区形象,改善业主居住环境,开发商准备对小区进行绿化.利用长度为64m的篱笆和一段小区围墙搭建如图所示的矩形花圃(接口忽略不计),分别用来种植不同的花卉.则花圃的一边AB为多长时,花圃的面积为192m2.
【分析】设AB=xm,则平行于墙的一边长为(64﹣4x)m,根据花圃的面积为192m2,即可得出关于x的一元二次方程,解之即可得出结论.
【解答】解:设AB=xm,则平行于墙的一边长为(64﹣4x)m,
依题意得:(64﹣4x)•x=192,
整理得:x8﹣16x+48=0,
解得:x1=7,x2=12.
答:花圃的一边AB长为4m或12m时,花圃的面积为192m6.
23.(8分)如图,在▱ABCD中,过A、B、C三点的⊙O交AD于点E,BE=BC.
(1)求证:△BEC∽△CED;
(2)若BC=10,DE=3.6,求⊙O的半径.
【分析】(1)证明两个等腰三角形相似,证明一个底角对应相等即可;
(2)利用直径构造直角三角形,从而涉及到半径(直径),再利用垂径定理即可解决问题.
【解答】(1)证明:∵BE=BC,
∴∠BEC=∠BCE
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠BCE=∠DEC,∠A+∠D=180°.
∴∠BEC=∠DEC
∵四边形ABCD内接于⊙O,
∴∠A+∠BCE=180°.
∴∠BCE=∠D
∴△BEC∽△CED
即得证.
(2)过点O作OF⊥CE,垂足为F,如下图.
∴CF=CE
∴直线OF垂直平分CE.
∵BE=BC,
∴直线OF经过点B.
∵△BEC∽△CED,又由(1)可知CE=CD,
∴=.
∵BC=10,DE=5.6,
∴CE=CD=6
∴CF=CE=3.
设⊙O的半径为r.
可得BF==,OF=.
在Rt△OCF中,OF2+CF7=OC2,
∴(﹣r)2+5=r2
∴r=
即圆的半径为.
24.(8分)快、慢两车分别从相距120千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,立即按原路返回,返回时的速度是去时速度的2倍1(千米)与出发后所用的时间x(小时)的关系如图所示.
请结合图象信息解答下列问题:
(1)慢车的速度是 40 千米/小时,快车的返回时速度是 120 千米/小时;
(2)画出快车距出发地的路程y2(千米)与出发后所用的时间x(小时)的函数图象;
(3)在快车返回途中,快、慢两车相距的路程为50千米时,慢车行驶了多少小时?
【分析】(1)由图象可知:甲、乙两地的距离为120千米,慢车从乙地到甲地所用时间为3小时,即可求出慢车的速度;设快车去时的速度为x千米/小时,则返回时的速度是2x千米/小时,根据题意得:,即可解答.
(2)开车从甲地开往乙地所用时间为:120÷60=2小时,快车返回甲地所用时间为:120÷120=1小时,即可画出图象.
(3)根据图象得:OA的函数关系式为y=40x,BC的函数关系式为y=120﹣120(x﹣2)=﹣120x+360;根据题意,得:﹣120x+360+40x=120+50,即可解答.
【解答】解:(1)由图象可知:甲、乙两地的距离为120千米,
∴慢车的速度为:120÷3=40(千米/小时),
设快车去时的速度为x千米/小时,则返回时的速度是2x千米/小时
,
解得:x=60,
检验:x=60是原方程的解,
∴快车返回时的速度是:60×2=120(千米/小时),
故答案为:40,120.
(2)如图:
(3)解:OA的函数关系式为y=40x,
BC的函数关系式为y=120﹣120(x﹣6)=﹣120x+360;
根据题意,得:
﹣120x+360+40x=120+50,解得:x=.
所以,慢车行驶,快、慢两车相距的路程为50千米.
25.(8分)一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为 26 件.
(2)当每件商品降价多少元时,该商店每天销售利润最大,最大利润是多少元?
【分析】(1)根据题意,可以求出降价3元时,平均每天销售数量;
(2)根据题意,可以得到利润与降价x的函数关系式,然后根据二次函数的性质,即可解答本题.
【解答】解:(1)由题意可得,
若降价3元,则平均每天销售数量为:20+2×5=26(件),
故答案为:26;
(2)设每件商品降价x元,销售利润为w元,
w=(40﹣x)(20+2x)=﹣2(x﹣15)8+1250,
∴当x=15时,w取得最大值,
答:当每件商品降价15元时,该商店每天销售利润最大.
26.(8分)已知二次函数y=a(x﹣m)(x﹣m﹣6)(a、m为常数,且a≠0),该函数图象顶点A的纵坐标为﹣9.
(1)求证:该函数的图象与x轴有两个公共点.
(2)若该函数图象与y轴交于点B(0,﹣5),求该函数的表达式.
(3)若该函数图象过点(﹣6,y1)与(2,y2),比较y1、y2的大小.
【分析】(1)令y=0,则a(x﹣m)(x﹣m﹣6)=0,求得该函数的图象与x轴有(m,0),(m+6,0)两个交点;
(2)求得对称轴,代入解析式即可求得a的值,根据函数图象与y轴交于点B(0,﹣5),即可求得m的值,从而求得抛物线的解析式;
(3)分三种情况讨论即可.
【解答】解:(1)令y=0,则a(x﹣m)(x﹣m﹣6)=7,
∴x1=m,x2=m+8,
∴该函数的图象与x轴有两个交点,分别为(m,(m+6;
(2)∵抛物线的对称轴为直线x==m+3,
∴当x=m+3时,y=﹣2a=﹣9,
∴a=1,
∵该函数图象与y轴交于B(8,﹣5),
∴y=(0﹣m)(4﹣m﹣6)=﹣5,即m7+6m+5=6,
∴(m+1)(m+5)=8,
解得,m1=﹣1,m2=﹣5,
当m=﹣5时,y=(x+2)(x﹣1)=x2+5x﹣5;
当m=﹣1时,y=(x+3)(x﹣5)=x2﹣5x﹣5;
∴该函数的表达式为y=x2+5x﹣5或y=x2﹣7x﹣5;
(3)∵抛物线开口向上,对称轴为直线x=m+3,
当m+7==﹣2时,
即当m=﹣5时,y4=y2,
当m>﹣5时,y5>y2,
当m<﹣5时,y7<y2.
27.(8分)如图,在△ABC中,AB=BC,过点C作∠ACD=∠ACB,且交⊙O于点D.连接BD交AC于点E,使得CF=CB,连接BF.
(1)求证:ED=EC.
(2)求证:BF是⊙O的切线.
(3)若点G为△BCD的内心,AE•AC=10.
①利用无刻度的直尺在图中画出点G的位置.(保留作图痕迹,不写作法)
②求AG的长.
【分析】(1)根据圆心角、弧、弦之间的关系进行证明即可;
(2)连接BO,根据垂径定理得到OB⊥AC,再根据角之间的关系推出∠BAC=∠ACD,从而推出AC∥BF,根据平行四边形的判定得到四边形ABFC是平行四边形,进而推出BF是⊙O的切线;
(3)①根据三角形的内心是三角形角平分线的交点,因此只需证明∠DBM=∠CBM,利用圆的垂径定理进行证明即可;
②根据圆周角定理得到∠ABE=∠ACB,从而推出△ABE∽△ACB,根据相似三角形的性质得到,从而解得AB=,再结合图形由三角形的外角性质及等量代换推出∠ABG=∠AGB,从而由等腰三角形的性质推出AG=AB=.
【解答】(1)证明:∵AB=BC,
∴=,
∴∠ACB=∠BDC,
又∠ACD=∠ACB,
∴∠ACD=∠BDC,
∴ED=EC;
(2)证明:如图1,
连接BO,
∵=,
∴OB⊥AC,
∵AB=BC,
∴∠BAC=∠BCA,
又∠ACD=∠ACB,
∴∠BAC=∠ACD,
∴AB∥CD,
∵CF=AB,
∴四边形ABFC是平行四边形,
∴AC∥BF,
∴OB⊥BF,
∵OB是⊙O的半径,
∴BF是⊙O的切线;
(3)如图2,
连接EO并延长交⊙O于点M,连接BM交AC于点G,
连接OD、OC,
∴点O在CD的垂直平分线上,
又根据(1)中的结论ED=EC,
∴点E在CD的垂直平分线上,
∴EM⊥DC,
∴=,
∴∠DBM=∠CBM,
∴BM是∠DBC的角平分线,
又∠ACD=∠ACB,
∴AC是∠BCD的角平分线,BM与AC交于点G,
∴点G是△BDC的内心;
②∵,
∴∠ABE=∠ACB,
又∠EAB=∠BAC,
∴△ABE∽△ACB,
∴,
又AE•AC=10,
解得AB=,
∵点G是△BDC的内心,
∴∠DBM=∠CBM,
∴∠ABE+∠DBM=∠ACB+∠CBM,
即∠ABG=∠AGB,
∴AG=AB=.
2023-2024学年江苏省南京市栖霞区重点学校九年级(上)10月月考数学试卷(含解析): 这是一份2023-2024学年江苏省南京市栖霞区重点学校九年级(上)10月月考数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年江苏省南京市栖霞区伯乐中学九年级(上)期初数学试卷(含解析): 这是一份2023-2024学年江苏省南京市栖霞区伯乐中学九年级(上)期初数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
江苏省南京市栖霞区五校2023届九年级上学期学情分析数学试卷(pdf版 含答案): 这是一份江苏省南京市栖霞区五校2023届九年级上学期学情分析数学试卷(pdf版 含答案),共12页。












