高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式学案

这是一份高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式学案，共9页。


授课提示：对应学生用书第24页
[教材提炼]
知识点一 一元二次不等式的概念
eq \a\vs4\al(预习教材，思考问题)
我们知道，方程x2＝1的一个解是x＝1，解集是{1，－1}，解集中的每一个元素均可使等式成立．那么什么是不等式x2＞1的解？你能举出一个解吗？你能写出不等式x2＞1的解集吗？
知识梳理 (1)一般地，我们把只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式(quadric inequality in ne unknwn)．一元二次不等式的一般形式是ax2＋bx＋c＞0或ax2＋bx＋c＜0，其中a，b，c均为常数，a≠0.
(2)一般地，对于二次函数y＝ax2＋bx＋c，我们把使ax2＋bx＋c＝0的实数x叫做二次函数y＝ax2＋bx＋c的零点．即一元二次方程的根是相应一元二次函数的零点．
知识点二 二次函数与一元二次方程、不等式的解的对应关系
eq \a\vs4\al(预习教材，思考问题)
函数y＝x2－1的零点与方程x2－1＝0及不等式x2－1＞0解之间有什么关系？
知识梳理 (1)
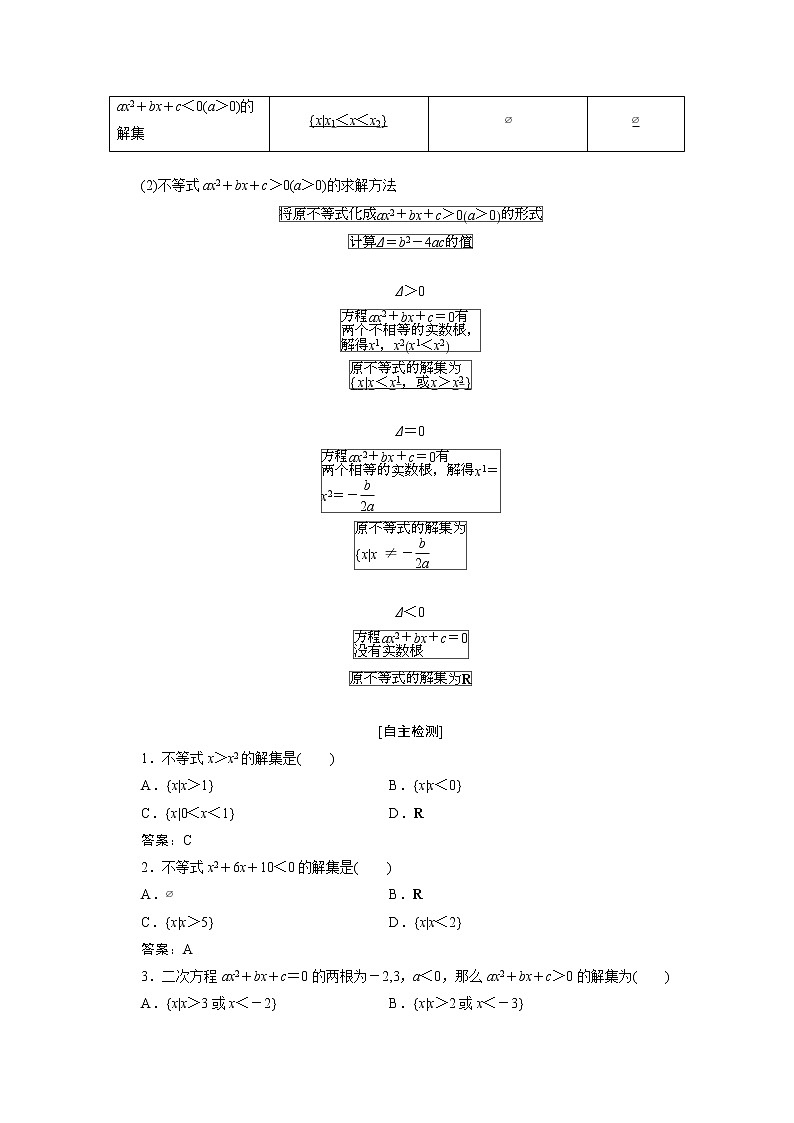
(2)不等式ax2＋bx＋c＞0(a＞0)的求解方法
eq \x(将原不等式化成ax2＋bx＋c＞0a＞0的形式)
eq \x(计算Δ＝b2－4ac的值)
Δ＞0
eq \x(\a\al(方程ax2＋bx＋c＝0有,两个不相等的实数根，,解得x1，x2x1＜x2))
eq \x(\a\al(原不等式的解集为,{x|x＜x1，或x＞x2}))
Δ＝0
eq \x(\a\al(方程ax2＋bx＋c＝0有,两个相等的实数根，解得x1＝,x2＝－\f(b,2a)))
eq \x(\a\al(原不等式的解集为,{x|x≠－\f(b,2a)))
Δ＜0
eq \x(\a\al(方程ax2＋bx＋c＝0,没有实数根))
eq \x(原不等式的解集为R)
[自主检测]
1．不等式x＞x2的解集是( )
A．{x|x＞1} B．{x|x＜0}
C．{x|0＜x＜1} D．R
答案：C
2．不等式x2＋6x＋10＜0的解集是( )
A．∅ B．R
C．{x|x＞5} D．{x|x＜2}
答案：A
3．二次方程ax2＋bx＋c＝0的两根为－2,3，a＜0，那么ax2＋bx＋c＞0的解集为( )
A．{x|x＞3或x＜－2} B．{x|x＞2或x＜－3}
C．{x|－2＜x＜3} D．{x|－3＜x＜2}
答案：C
4．不等式－x2＋x－2＜0的解集为________．
答案：R
授课提示：对应学生用书第25页
探究一 一元二次不等式的解法
[例1] 解下列不等式．
(1)－x2＋2x－eq \f(2,3)＞0；
(2)－eq \f(1,2)x2＋3x－5＞0；
(3)4x2－18x＋eq \f(81,4)≤0.
[解析] (1)两边都乘以－3，得3x2－6x＋2＜0，
∵3＞0，Δ＝36－24＝12＞0，且方程3x2－6x＋2＝0的根是x1＝1－eq \f(\r(3),3)，x2＝1＋eq \f(\r(3),3).
∴原不等式的解集是{x|1－eq \f(\r(3),3)＜x＜1＋eq \f(\r(3),3)}．
(2)不等式可化为x2－6x＋10＜0，
Δ＝(－6)2－4×10＝－4＜0，
∴原不等式的解集为∅.
(3)不等式可化为16x2－72x＋81≤0，
即(4x－9)2≤0，∵4x－9＝0时，x＝eq \f(9,4).
∴原不等式的解集为{x|x＝eq \f(9,4)}.
解一元二次不等式的一般步骤
(1)通过对不等式变形，使二次项系数大于零；
(2)计算对应方程的判别式；
(3)求出相应的一元二次方程的根，或根据判别式说明方程没有实根；
(4)根据函数图象与x轴的相关位置写出不等式的解集.
1．求不等式2x2－3x－2≥0的解集．
解析：∵2x2－3x－2＝0的两解为x1＝－eq \f(1,2)，x2＝2，且a＝2＞0，
∴不等式2x2－3x－2≥0的解集是eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≤－\f(1,2)，或x≥2)))).
2．解不等式－x2＋2x－3＞0.
解析：不等式可化为x2－2x＋3＜0.
因为Δ＝(－2)2－4×3＝－8＜0，
方程x2－2x＋3＝0无实数解，
而y＝x2－2x＋3的图象开口向上，
所以原不等式的解集是∅.
探究二 含参数的一元二次不等式
[例2] 解关于x的不等式x2－(a＋a2)x＋a3＞0(a∈R)．
[解析] 原不等式可化为(x－a)(x－a2)＞0.
当a＜0时，a＜a2，原不等式的解集为{x|x＜a，或x＞a2}；
当a＝0时，x2＞0，原不等式的解集为{x|x≠0}；
当0＜a＜1时，a2＜a，原不等式的解集为{x|x＜a2，或x＞a}；
当a＝1时，a2＝a，原不等式的解集为{x|x≠1}；
当a＞1时，a＜a2，原不等式的解集为{x|x＜a，或x＞a2}．
综上所述：
当a＜0或a＞1时，原不等式的解集为{x|x＜a，或x＞a2}；
当0＜a＜1时，原不等式的解集为{x|x＜a2，或x＞a}；
当a＝0时，解集为{x|x≠0}；
当a＝1时，解集为{x|x≠1}．
解含参数的不等式，可以按常规思路进行：先考虑开口方向，再考虑判别式的正负，最后考虑两根的大小关系，当遇到不确定因素时再讨论．
将本例不等式变为：解关于x的不等式ax2－(a＋1)x＋1＜0(a∈R，a＞0)．
解析：因为a＞0，所以原不等式等价于eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＜0.
①当a＝1时，eq \f(1,a)＝1，eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＜0无解；
②当a＞1时，eq \f(1,a)＜1，解eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＜0，得eq \f(1,a)＜x＜1；
③当0＜a＜1时，eq \f(1,a)＞1，解eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,a)))(x－1)＜0，
得1＜x＜eq \f(1,a).
综上，
a＞1时，不等式的解集为{x|eq \f(1,a)＜x＜1}；
a＝1时，不等式的解集为∅；
0＜a＜1时，不等式的解集为{x|1＜x＜eq \f(1,a)}．
探究三 三个二次之间的关系
[例3] [教材P52例1、例2的拓展探究]
(1)已知解集求函数
若不等式y＝ax2－x－c＞0的解集为(－2,1)，则函数的图象为( )
[解析] 因为不等式的解集为(－2,1)，所以a＜0，排除C，D；又与坐标轴交点的横坐标为－2,1，故选B.
[答案] B
(2)已知方程的根或函数零点求不等式
若函数y＝x2－ax＋1有负数零点，则a的范围为________．
[解析] 有零点，
∴Δ＝a2－4≥0，
∴a≥2或a≤－2，
∵f(0)＝1，要使x2－ax＋1＝0有负根，则对称轴x＝eq \f(a,2)＜0，即a＜0.
∴a≤－2.
[答案] a≤－2
(3)已知解集求不等式
已知x2＋px＋q＜0的解集是eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(－\f(1,2)＜x＜\f(1,3)))))，解关于x的不等式qx2＋px＋1＞0.
[解析] 由已知得，x1＝－eq \f(1,2)，x2＝eq \f(1,3)是方程x2＋px＋q＝0的根，
∴－p＝－eq \f(1,2)＋eq \f(1,3)，q＝－eq \f(1,2)×eq \f(1,3)，
∴p＝eq \f(1,6)，q＝－eq \f(1,6).
∵不等式qx2＋px＋1＞0，
∴－eq \f(1,6)x2＋eq \f(1,6)x＋1＞0，
即x2－x－6＜0，∴－2＜x＜3，
故不等式qx2＋px＋1＞0的解集为{x|－2＜x＜3}．
应用三个“二次”之间的关系解题的思想
一元二次不等式与其对应的函数与方程之间存在着密切的联系，即给出了一元二次不等式的解集，则可知不等式二次项系数的符号和相应一元二次方程的根．在解决具体的数学问题时，要注意三者之间的相互联系，并在一定条件下相互转换．
授课提示：对应学生用书第26页
分久必合——分类讨论思想解含参数不等式eq \x(►逻辑推理)
含有参数的一元二次不等式，因为含有参数，便大大增加了问题的复杂程度．分类讨论是解决这类问题的主要方法，确定分类讨论的标准时，要着重处理好以下三点：
(1)讨论的“时刻”，即在什么时候才开始进行讨论．要求转化必到位，过早或过晚讨论都会使问题更加复杂化．
(2)讨论的“点”，即以哪个量为标准进行讨论．若把握不好这一类，问题就不能顺利解决．
(3)考虑要周到，即讨论对象的各种情况都要加以分析，给出结论．
1．讨论二次项系数型为主
当二次项系数为字母时，首先要讨论二次项系数是否为0，若二次项系数为0，则该不等式变为一次不等式；若二次项系数不为0，解集则与二次项系数的正负相关．
[典例] 解关于x的不等式，ax2＋(1－a)x－1＞0.
[解析] 原不等式化为(x－1)(ax＋1)＞0
(1)当a＝0时，原不等式为x－1＞0，∴x＞1，
(2)当a＞0时，原不等式为(x－1)(x＋eq \f(1,a))＞0.
两根为1与－eq \f(1,a)且1＞－eq \f(1,a)，
∴得x＞1或x＜－eq \f(1,a)；
(3)当a＜0时，原不等式化为(x－1)(x＋eq \f(1,a))＜0
两根为1与－eq \f(1,a)，
又∵当－1＜a＜0时，－eq \f(1,a)＞1，
∴得1＜x＜－eq \f(1,a).
当a＝－1时，不等式为(x－1)2＜0，解集为∅，
当a＜－1时，－eq \f(1,a)＜1，∴得－eq \f(1,a)＜x＜1.
综上，当a＞0时，解集为{x|x＞1，或x＜－eq \f(1,a)}；
当a＝0时，解集为{x|x＞1}；
当－1＜a＜0时，解集为{x|1＜x＜－eq \f(1,a)}；
当a＝－1，解集为∅；
当a＜－1时，解集为{x|－eq \f(1,a)＜x＜1}．
规律总结
解二次项含参数的一元二次不等式一定要对参数大于0，等于0和小于0展开讨论．
2．讨论判别式型为主
当二次不等式中有字母，且不易观察出所对应方程是否有实根，此时应对方程有无实根进行讨论．
[典例] 解关于x的不等式：2x2＋ax＋2＞0.
[解析] Δ＝a2－16＝(a－4)(a＋4)．
(1)当a＞4或a＜－4时，Δ＞0，方程2x2＋ax＋2＝0的两根为x1＝eq \f(1,4)(－a－eq \r(a2－16))，x2＝eq \f(1,4)(－a＋eq \r(a2－16))．
原不等式的解集为
eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x＜\f(1,4)－a－\r(a2－16)或x＞\f(1,4)－a＋\r(a2－16))))).
(2)当a＝±4时，Δ＝0，方程只有一根x＝－eq \f(a,4)，
∴原不等式的解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x∈R且x≠－\f(a,4))))).
(3)当－4＜a＜4时，Δ＜0，方程无根，∴原不等式的解集为R.
规律总结
若一元二次方程判别式符号不确定，应分Δ＞0、Δ＝0、Δ＜0讨论．
3．讨论根的大小型为主
当一元二次不等式中有字母，而导致根的大小不易区别时，应通过作差法，由根的大小确定字母范围．
[典例] 解关于x的不等式：x2－2x＋1－a2≥0.
[解析] 原不等式等价于(x－1－a)(x－1＋a)≥0.
①当a＞0时，1＋a＞1－a，所以原不等式的解集为{x|x≥1＋a，或x≤1－a}．
②当a＝0时，原不等式的解集为全体实数R.
③当a＜0时，1－a＞1＋a，原不等式的解集为{x|x≥1－a，或x≤1＋a}．
规律总结
当不等式对应方程根的大小不确定时，必须讨论根的大小，以确定不等式的解集．
在解关于含参数的一元二次不等式时，往往要对参数进行分类讨论，为了做到分类“不重不漏”，讨论需从如下三个方面进行考虑：
(1)关于不等式类型的讨论：二次项系数a＞0，a＜0，a＝0.
(2)关于不等式对应的方程是否有根的讨论：二根(Δ＞0)，一根(Δ＝0)，无根(Δ＜0)．
(3)关于不等式对应的方程根的大小的讨论：x1＞x2，x1＝x2，x1＜x2.
内 容 标 准
学 科 素 养
1.理解一元二次方程、一元二次不等式与二次函数的关系．
数学抽象
直观想象
逻辑推理、数学运算
2.掌握图象法解一元二次不等式．
3.会对含参数的一元二次不等式分类讨论.
Δ＝b2－4ac
Δ＞0
Δ＝0
Δ＜0
y＝ax2＋bx＋c(a＞0)的图象
ax2＋bx＋c＝0(a＞0)的根
有两个不相等的实数根x1，x2(x1＜x2)
有两个相等的实数根x1＝x2＝－eq \f(b,2a)
没有实数根
ax2＋bx＋c＞0(a＞0)的解集
{x|x＜x1，或x＞x2}
{x|x≠－eq \f(b,2a)}
R
ax2＋bx＋c＜0(a＞0)的解集
{x|x1＜x＜x2}
∅
∅