2020-2021学年5.1.1 数列的概念教学设计

课程目标

学科素养

A.理解数列的有关概念与数列的表示方法.

B.掌握数列的分类.

C.理解数列的函数特征,掌握判断数列增减性的方法.

D.掌握数列通项公式的概念及其应用,能够根据数列的前几项写出数列的一个通项公式.

1.数学抽象：数列的概念及表示、数列的分类

2.逻辑推理：求数列的通项公式

3.数学运算：运用数列通项公式求特定项

4.数学建模：数列的概念

教学过程

教学设计意图

核心素养目标

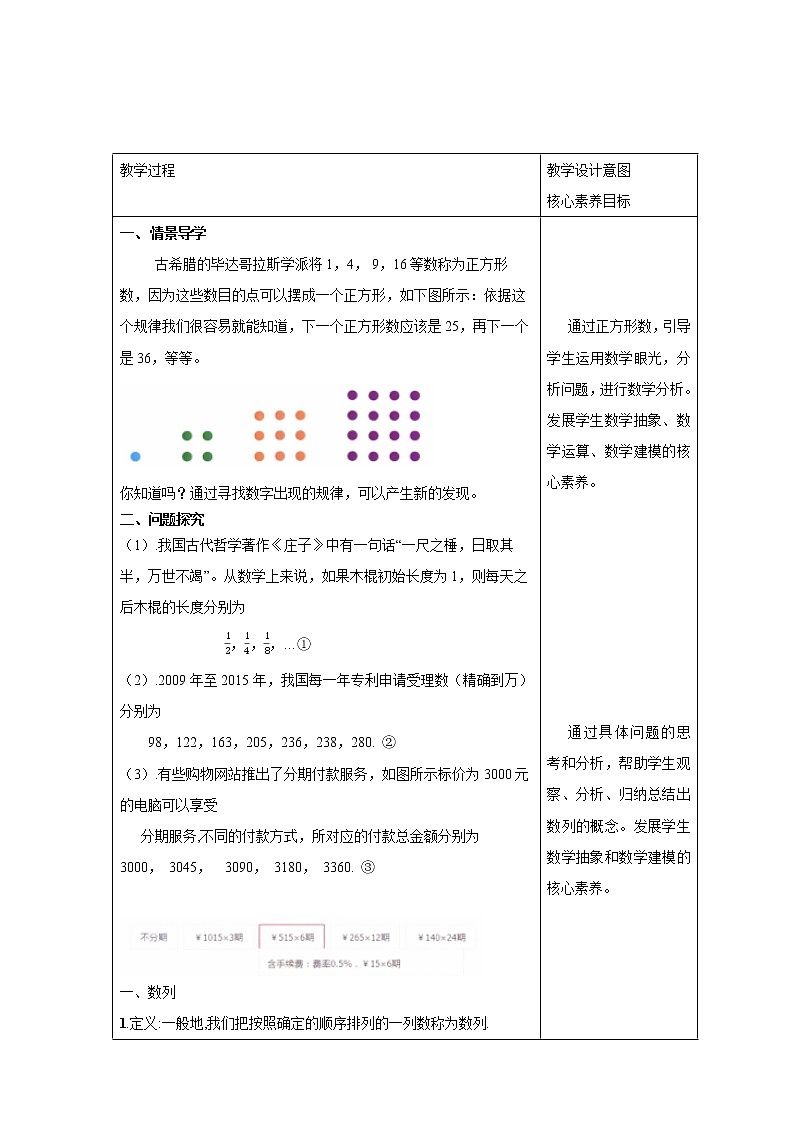
一、    情景导学

古希腊的毕达哥拉斯学派将1，4， 9，16等数称为正方形数，因为这些数目的点可以摆成一个正方形，如下图所示：依据这个规律我们很容易就能知道，下一个正方形数应该是25，再下一个是36，等等。

你知道吗？通过寻找数字出现的规律，可以产生新的发现。

二、问题探究

（1）.我国古代哲学著作《庄子》中有一句话“一尺之棰，日取其半，万世不竭”。从数学上来说，如果木棍初始长度为1，则每天之后木棍的长度分别为

               ，，，…①
（2）.2009年至2015年，我国每一年专利申请受理数（精确到万）分别为
    98，122，163，205，236，238，280. ②

（3）.有些购物网站推出了分期付款服务，如图所示标价为3000元的电脑可以享受

   分期服务,不同的付款方式，所对应的付款总金额分别为
3000， 3045，  3090， 3180， 3360. ③

一、数列

1.定义:一般地,我们把按照确定的顺序排列的一列数称为数列.

2.项:数列中的每一个数叫做这个数列的项.数列的第一个位置上的数叫做这个数列的第1项,常用符号a1表示;第二个位置上的数叫做这个数列的第2项,用a2表示……第n个位置上的数叫做这个数列的第n项,用an表示.其中第1项也叫做首项.

3.表示:数列的一般形式是a1,a2,…,an,…,简记为{an}.

点睛：(1)数列是按一定的“顺序”排列的一列数,有序性是数列的基本属性.

数相同而顺序不同的两个数列是不相同的数列,

例如1,2,3,…与3,2,1…就是不同的数列.

(2)符号{an}和an是不同的概念,{an}表示一个数列,而an表示数列中的第n项.

二、数列的分类

1. 下列叙述正确的是(　　)

A.所有数列可分为递增数列和递减数列两类

B.数列中的数由它的位置序号唯一确定

C.数列1,3,5,7可表示为{1,3,5,7}

D.同一个数在数列中不可能重复出现

解析:按项的变化趋势,数列可分为递增数列、递减数列、常数列、摆动数列等数列,A错误;数列1,3,5,7与由实数1,3,5,7组成的集合{1,3,5,7}是两个不同的概念,C错误;同一个数在数列中可能重复出现,如2,2,2,…表示由实数2构成的常数列,D错误;对于给定的数列,数列中的数由它的位置序号唯一确定,B正确.

答案:B

三、数列的通项公式

      如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.

点睛：(1)数列的通项公式实际上是一个以正整数集N*(或它的有限子集){1,2,…,n}为定义域的函数表达式.

(2)并不是所有的数列都有通项公式.

(3)同一数列的通项公式,其表达形式可以是不唯一的,例如数列

-1,1,-1,1,-1,1,…的通项公式可以写成an=(-1)n,an=(-1)n+2,an=cos nπ等.

1.若数列{an}的通项公式是an=n2-1,则该数列的第10项a10=　　　　　,224是该数列的第　　　　　项. 

解析:a10=102-1=99.令an=n2-1=224,解得n=15,即224是该数列的第15项.

答案:99　15

三、典例解析

例1. 根据下列数列的通项公式，写出数列的第2项和第5项；

（1）     （2） .

解:（1）由通项公式可知

1.

.
（2）由通项公式可知

  0.

例2. 写出以下各数列{an}的一个通项公式：

(1),…;

(2)1,3,5,7,9,…;

(3)0,2,0,2,0,…;

(4)-,-, -….

分析:观察、分析,寻找数列的每一项与其所在项的序号之间的关系.

解:(1)观察数列的前5项可知，每一项都是序号的2倍，因此数列的一个通项公式为an=2n.

(2)因为这个数列每一项都比（1）中数列的每一项小1，

因此数列的一个通项公式为an=2n-1

（3）因为数列的第1,3,5项都是0，而第2,4项都是2.

因此它的一个通项公式为an=

（4）忽略正负号时，数列每一项的分子构成的数列是2,4,6,8,10,…其中每一个数都是序号的2倍；而且，数列每一项的分母都是分子平方减去1.又因为负号、正号是交替出现的。因此它的一个通项公式为an=(-1)n

根据数列的前几项写通项公式的具体思路为:

(1)先统一项的结构,如都化成分数、根式等.

(2)分析这一结构中变化的部分与不变的部分,探索变化部分的规律与对应序号间的关系.

(3)对于符号交替出现的情况,可先观察其绝对值,再用(-1)k处理符号.

(4)对于周期出现的数列,考虑利用周期函数的知识解答.

2.常见数列的通项公式

(1)数列-1,1,-1,1,…的一个通项公式是an=(-1)n,数列1,-1,1,-1,…的一个通项公式是an=(-1)n+1或(-1)n-1.

(2)数列1,2,3,4,…的一个通项公式是an=n.

(3)数列1,3,5,7,…的一个通项公式是an=2n-1.

(4)数列2,4,6,8,…的一个通项公式是an=2n.

(5)数列1,2,4,8,…的一个通项公式是an=2n-1.

(6)数列1,4,9,16,…的一个通项公式是an=n2.

(7)数列1,3,6,10,…的一个通项公式是an=.

(8)数列1,,…的一个通项公式是an=.

跟踪训练1.写出下列数列的一个通项公式,使它的前4项分别是下列各数:

(1)1,;

(2)2,4,6,8;

(3)3,5,9,17;

(4);

(5)7,77,777,7 777.

解:(1)an=;(2)an=2n+;

(3)an=2n+1;(4)an=;

(5)an=(10n-1).

（1）已知函数你能根据这个函数构造出一个数列吗？

（2）你能总结出一般数列与函数的关系吗？

分析:令=1,2,3,4，…，n…，可得到数列

2，，1，…，，….，

四、数列与函数

数列{an}是从正整数集N*(或它的有限子集{1,2，…，n})到实数集R的函数，

其自变量是序号n，对应的函数值是数列的第n项an，

记为an＝f(n)．

另一方面，对于函数y＝f(x)，

如果f(n)(n∈N*)有意义，

那么                  构成了一个数列{f(n)}．

f(1)，f(2)，…，f(n)，…

例3.已知函数设数列{an}的通项公式为an=其中n∈N*

（1）求证：<1 ;

（2）判断{an}是递增数列还是递减数列，并说明理由.

解：（1）由题意可知an=

又因为n∈N* ，所以0<，

因此<1 ;即<1.

（2）因为= （ ）（

又因为> ，所以>0，

从而>0，即

因此{an}是递增数列.

数列增减性的判定方法

(1)作差比较法

①若an+1-an>0恒成立,则数列{an}是递增数列;

②若an+1-an<0恒成立,则数列{an}是递减数列;

③若an+1-an=0恒成立,则数列{an}是常数列.

(2)作商比较法

跟踪训练2.已知函数f(x)= x- 数列{an}满足f(an)=-2n,且an>0.

(1)求数列{an}的通项公式;

(2)判断数列{an}是递增数列还是递减数列,并说明理由.

分析：先根据已知条件解方程求an,再利用作差法或作商法判断数列{an}是递增数列还是递减数列.

解:(1)∵f(x)=x-,f(an)=-2n,

∴an-=-2n,即+2nan-1=0,

解得an=-n±,

∵an>0,∴an=-n.

(2)(方法一:作差法)

∵an+1-an=-(n+1)-(-n)

=-1

=-1=-1,

又>n+1,>n,

∴<1.

∴an+1-an<0,即an+1<an.

∴数列{an}是递减数列.

(方法二:作商法)

∵an>0,∴=<1.

∴an+1<an.

∴数列{an}是递减数列.

通过正方形数，引导学生运用数学眼光，分析问题，进行数学分析。发展学生数学抽象、数学运算、数学建模的核心素养。

通过具体问题的思考和分析，帮助学生观察、分析、归纳总结出数列的概念。发展学生数学抽象和数学建模的核心素养。

通过数列概念的解读，并与集合、函数概念的比较，深化对数列概念的理解。发展学生数学抽象、逻辑推理和数学建模的核心素养。

通过典型例题，加深学生对数列概念及通项公式的理解和运用，发展学生逻辑推理，直观想象、数学抽象和数学运算的核心素

通过典型例题，帮助灵活运用数列的概念解决问题，发展学生逻辑推理，直观想象、数学抽象和数学运算的核心素养。

三、达标检测

1.以下四个数中,哪个数是数列{n(n+1)}中的一项(　　)

A.380          B.39             C.32             D.23

解析:n(n+1)是这个数列的通项公式,即an=n(n+1).

∵380=19×20=19×(19+1),

∴380是该数列中的第19项,或者令n(n+1)=380,得n=19,是整数,符合题意.故选A.

答案:A

2.在数列1,1,2,3,5,8,13,x,34,…中,x的值是(　　)

A.19        B.20       C.21                D.22

解析:观察数列可得规律1+1=2,1+2=3,2+3=5,…,8+13=x=21,13+21=34,∴x=21,故选C.

答案:C

3.数列0,1,0,-1,0,1,0,-1,…的一个通项公式为(　　)

A. B.cos C.cosπ D.cosπ

解析:当n=4时,=1≠-1,cos=cos=cos 2π=1≠-1,排除A,B;当n=2时,cos=cos=0≠1,排除C;经检验,D项符合题意.故选D.

答案:D

4.已知数列{an}中,an=-2n2+31n+9(n∈N+),则{an}中的最大项为　　　. 

解析:∵an=-2n2+31n+9=-2(n-)2+(n∈N+),

又7<<8,∴a7=128,a8=129,a7<a8,

∴数列{an}中的最大项为129.

答案:129

5.分别写出下列数列的一个通项公式:

(1)-1,3,-5,7,-9,…;

(2)4,-,2,-,…;

(3)1,1,,…;

(4),3,,3,….

解:(1)因为数列的各项是负正项交替出现的,所以用(-1)n来调节,数列各项的绝对值可以分成整数、分数的分子和分母三部分,整数部分是1,3,5,7,9,为奇数,分数的分子是1,2,3,4,5,正好是序号,分母是4,9,16,25,36,正好是平方数,这样我们可以归纳出数列的一个通项

公式为an=(-1)n.

(2)将数列前4项改写成分数的形式,-,-,可得该数列的一个通项公式an=(-1)n+1.

(3)原数列可写成,…,得该数列的一个通项公式为an=.

(4)原数列可写成,…,

得该数列的一个通项公式为an=.

6.在数列{an}中,已知an=(n∈N*).

(1)写出a10,an+1.

(2)79是不是该数列中的项?如果是,是第几项?

解:(1)a10=;

an+1=.

(2)令an==79,解得n=15(n=-16舍去),

所以79是该数列中的项,并且是第15项.

7.已知数列{an}的通项公式an=(k∈R).

(1)当k=1时,判断数列{an}的单调性;

(2)若数列{an}是递减数列,求实数k的取值范围.

分析:对于(1),因为已知数列的通项公式,所以可以通过比较数列的相邻两项an与an+1的大小来确定数列的单调性;

对于(2),可根据数列是递减数列,得出an与an+1的大小关系,从而确定k的取值范围.

解:(1)当k=1时,an=,所以an+1=,

所以an+1-an=>0,

故数列{an}是递增数列.

(2)若数列{an}是递减数列,则an+1-an<0恒成立,

即an+1-an=<0恒成立.

因为(2n+5)(2n+3)>0,所以必有3k<0,故k<0.

通过练习巩固本节所学知识，通过学生解决问题，发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。

四、小结

五、课时练

通过总结，让学生进一步巩固本节所学内容，提高概括能力。