

数学人教B版 (2019)11.1.6 祖暅原理与几何体的体积导学案及答案
展开【学习重点】
利用祖暅原理推导柱体、锥体、球的体积公式、并运用体积公式解决简单的实际问题
【学习难点】
空间问题转化为平面问题解决问题,割补转化法求几何体的体积
问题1:祖暅原理
知识点1:祖暅原理
1.祖暅原理:幂势既同,则积不容异.
2.含义:夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任意平面所截,两个截面的面积总相等,那么这两个几何体的体积一定相等.如图所示.
思考:
1.夹在两个平行平面间的三棱锥和三棱柱,如果它们的底面积相等,那么这两个几何体的体积是否相等?
2.若三棱柱ABC-A1B1C1与圆柱O′O的高相等,且△ABC的面积与底面圆O的面积相等,那么它们的体积是否相等?
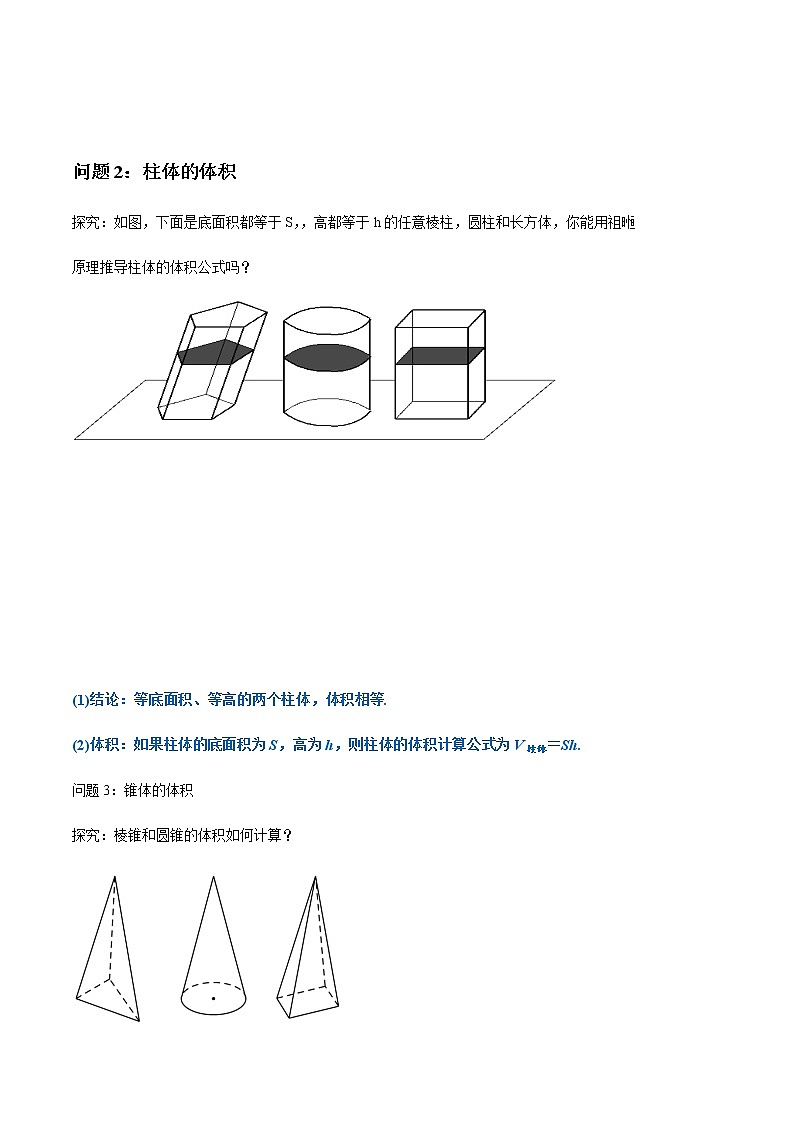
问题2:柱体的体积
探究:如图,下面是底面积都等于S,,高都等于h的任意棱柱,圆柱和长方体,你能用祖暅
原理推导柱体的体积公式吗?
(1)结论:等底面积、等高的两个柱体,体积相等.
(2)体积:如果柱体的底面积为S,高为h,则柱体的体积计算公式为V柱体=Sh.
问题3:锥体的体积
探究:棱锥和圆锥的体积如何计算?
(1)结论:等底面积、等高的两个锥体,体积相等.
(2)体积:如果锥体的底面积为S,高为h,则椎体的体积计算公式为V椎体=eq \f(1,3)Sh.
【对点快练】
1.圆锥的底面半径为4,母线长为6,则体积为________
例1.如图所示,长方体中,求棱锥的体积和长方体的体积之比.
问题4:台体的体积
探究:棱台、圆台的体积如何求解?
例2.已知四棱台上下底面面积分别为,而且高为,求这个棱台的体积。
知识点:
台体(棱台与圆台)的体积:如果台体的上、下底面面积分别为S1、S2,高为h,则台体的体积计算公式为V台体=eq \f(1,3)(S2+eq \r(S2S1)+S1)h.
【对点快练】
已知棱台的上、下底面面积分别为4,16,高为3,则棱台的体积为________.
思考:柱体、锥体、球体的体积有什么关系?
例3.(1)过长方体的一个顶点的三条棱长的比为1∶2∶3,对角线的长为2eq \r(14),求这个长方体的体积;
(2)如图,在三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1-ABC,三棱锥B-A1B1C,三棱锥C-A1B1C1的体积之比.
例4. (1)已知圆柱的侧面展开图是长、宽分别为2π和4π的矩形,求这个圆柱的体积;
(2)如图,圆台高为3,轴截面中母线AA1与底面直径AB的夹角为60°,轴截面中一条对角线垂直于腰,求圆台的体积.
问题5:球的体积
尝试与发现:
(1)你能想办法测出一个乒乓球的体积吗?
(2)如图所示是底面积和高都相等的两个几何体,左边是半球,右边是圆柱被挖去一个倒立的圆锥剩余的部分,用平行于半球与圆柱底面的平面去截这两个几何体,分别指出截面的形状,并讨论两个截面面积的大小关系,由此你能得到球的体积公式吗?
知识点:
如果球的半径为R,那么球的体积计算公式为V球=eq \f(4πR3,3)
【对点快练】
1.若将球的半径扩大到原来的2倍,则它的体积增大到原来的( )
A.2倍 B.4倍
C.8倍 D.16倍
2.已知球的表面积是16π,则该球的体积为________.
问题6:组合体
知识点:
1.概念:由简单几何体组合而成的几何体一般称为组合体.常见的组合体大多是由柱、锥、台、球等几何体组成的.
2.求组合体的体积(或表面积)时,只需要算出其中每个几何体的体积(或表面积),然后再处理即可.
【对点快练】
1.如图所示的组合体,其结构特征是( )
A.两个圆锥
B.两个圆柱
C.一个棱锥和一个棱柱
D.一个圆锥和一个圆柱
2.如图是由一个圆锥和一个半球组成的组合体,数据如图,则该组合体的体积为________.
例5.如图所示,某铁质零件由一个正四棱柱和一个球组成,已知正四棱柱底面边长与球的直径均为1cm,正四棱柱的高位2cm,现有这种零件一盒共50kg,取铁的密度位
(1)估计有多少个这样的零件?
(2)如果要给这盒两件的每个零件表面涂上一种特殊的材料,则需要能涂多少平方厘米的材料(球和棱柱接口处面积不计,结果精确到1)?
【变式练习】
如图所给图形及数据(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.
考点
学习目标
祖暅原理
了解祖暅原理的内容,掌握利用祖暅原理推导柱体、锥体、球的体积公式的过程
柱体、锥体、台体、球的体积公式
掌握柱体、锥体、台体、球的体积公式、能运用公式解决简单的实际问题
组合体的体积、表面积
了解组合体的概念,掌握求组合体表面积、体积的方法,并解决实际应用问题
高中数学人教B版 (2019)必修 第四册11.1.6 祖暅原理与几何体的体积学案: 这是一份高中数学人教B版 (2019)必修 第四册11.1.6 祖暅原理与几何体的体积学案,共7页。学案主要包含了学习目标,学习过程,学习小结,精炼反馈等内容,欢迎下载使用。
高中人教B版 (2019)第十一章 立体几何初步11.1 空间几何体11.1.2 构成空间几何体的基本元素导学案: 这是一份高中人教B版 (2019)第十一章 立体几何初步11.1 空间几何体11.1.2 构成空间几何体的基本元素导学案,共12页。学案主要包含了学习重点,学习难点,变式练习等内容,欢迎下载使用。
人教B版 (2019)必修 第四册11.1.4 棱锥与棱台导学案及答案: 这是一份人教B版 (2019)必修 第四册11.1.4 棱锥与棱台导学案及答案,共8页。学案主要包含了学习重点,学习难点,变式练习,概念辨析等内容,欢迎下载使用。













