三年（2019-2021）高考数学（理）真题分项汇编之专题19不等式选讲（解析版）

专题19    不等式选讲

1．【2021年全国高考甲卷数学（理）试题】已知函数．

（1）画出和的图像；

（2）若，求a的取值范围．

【答案】（1）图像见解析；（2）

【分析】（1）分段去绝对值即可画出图像；

（2）根据函数图像数形结和可得需将向左平移可满足同角，求得过时的值可求.

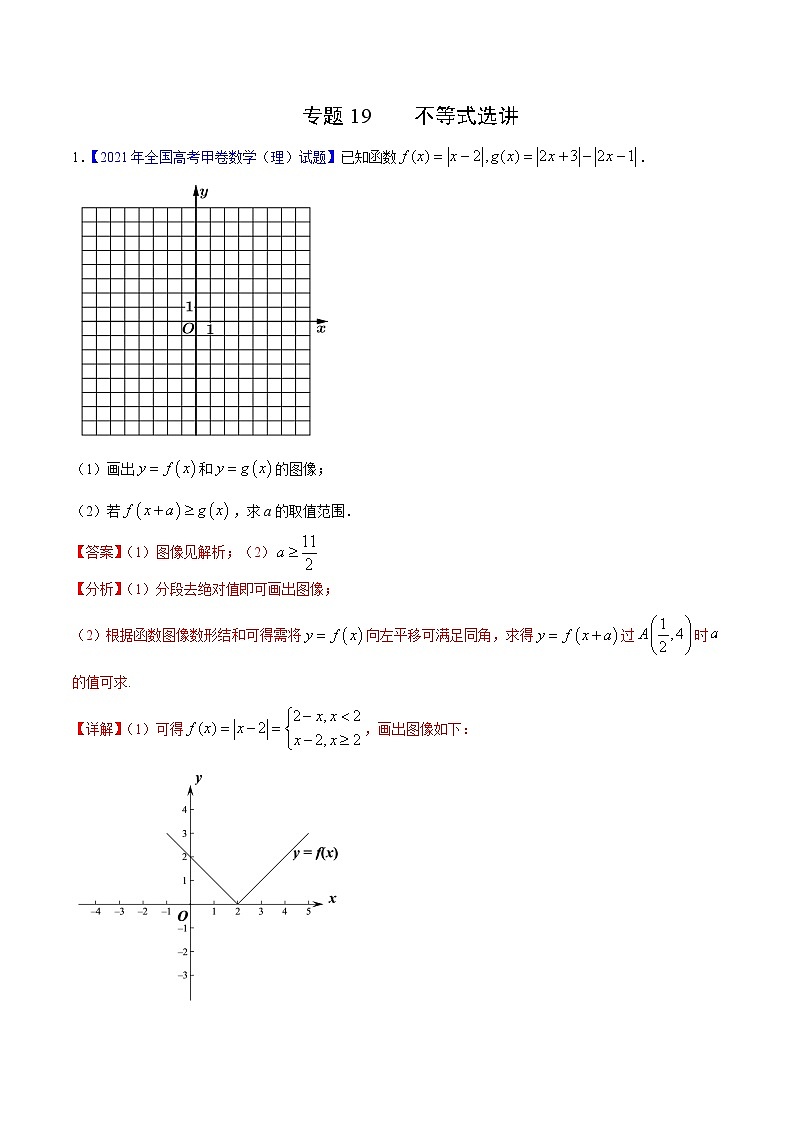
【详解】（1）可得，画出图像如下：

，画出函数图像如下：

（2），

如图，在同一个坐标系里画出图像，

是平移了个单位得到，

则要使，需将向左平移，即，

当过时，，解得或（舍去），

则数形结合可得需至少将向左平移个单位，.

【点睛】

关键点睛：本题考查绝对值不等式的恒成立问题，解题的关键是根据函数图像数形结合求解.

2．【2021年全国高考乙卷数学（理）试题】已知函数．

（1）当时，求不等式的解集;

（2）若，求a的取值范围．

【答案】（1）.（2）.

【分析】

（1）利用绝对值的几何意义求得不等式的解集.

（2）利用绝对值不等式化简，由此求得的取值范围.

【详解】

（1）当时，，表示数轴上的点到和的距离之和，

则表示数轴上的点到和的距离之和不小于，

当或时所对应的数轴上的点到所对应的点距离之和等于6，

∴数轴上到所对应的点距离之和等于大于等于6得到所对应的坐标的范围是或，

所以的解集为.

（2）依题意，即恒成立，

，

当且仅当时取等号，,

故，

所以或，

解得.

所以的取值范围是.

【点睛】

解绝对值不等式的方法有零点分段法、几何意义法．解含有两个绝对值，且其中的的系数相等时，可以考虑利用数轴上绝对值的几何意义求解；利用绝对值三角不等式求最值也是常见的问题，注意表述取等号的条件.

3．【2020年高考全国Ⅰ卷理数】[选修4—5：不等式选讲]（10分）

 已知函数．

（1）画出的图像；

（2）求不等式的解集．

【解析】（1）由题设知

的图像如图所示．

（2）函数的图像向左平移1个单位长度后得到函数的图像．

的图像与的图像的交点坐标为．

由图像可知当且仅当时，的图像在的图像上方，

故不等式的解集为．

4．【2020年高考全国II卷理数】[选修4—5：不等式选讲]（10分）

已知函数f(x)= |x-a2|+|x-2a+1|．

（1）当a=2时，求不等式f(x)≥4的解集；

（2）若f(x)≥4，求a的取值范围．

【解析】（1）当时，

因此，不等式的解集为．

（2）因为，故当，即时，．所以当a≥3或a≤-1时，．

当-1<a<3时，，

所以a的取值范围是．

5．【2020年高考全国III卷理数】[选修4—5：不等式选讲]（10分）

设a，b，c∈R，，．

（1）证明：；

（2）用表示a，b，c的最大值，证明：≥．

【解析】（1）由题设可知，a，b均不为零，所以

.

（2）不妨设max{a，b，c}=a，因为，所以a>0，b<0，c<0.由，可得，故，所以.

6．【2020年高考江苏】[选修4-5：不等式选讲]（本小题满分10分）

设，解不等式．

【解析】当x>0时，原不等式可化为，解得；

当时，原不等式可化为，解得；

当时，原不等式可化为，解得．

综上，原不等式的解集为．

7．【2019年高考全国Ⅰ卷理数】已知a，b，c为正数，且满足abc=1．证明：

（1）；

（2）．

【答案】（1）见解析；（2）见解析．

【解析】（1）因为，又，故有

．

所以．

（2）因为为正数且，故有

=24．

所以．

【名师点睛】本题考查利用基本不等式进行不等式的证明问题，考查学生对于基本不等式的变形和应用能力，需要注意的是在利用基本不等式时需注意取等条件能否成立．

8．【2019年高考全国Ⅱ卷理数】已知

（1）当时，求不等式的解集；

（2）若时，，求的取值范围．

【答案】（1）；（2）

【解析】（1）当a=1时，．

当时，；当时，．

所以，不等式的解集为．

（2）因为，所以．

当，时，．

所以，的取值范围是．

【名师点睛】本题主要考查含绝对值的不等式，熟记分类讨论的方法求解即可，属于常考题型．

9．【2019年高考全国Ⅲ卷理数】设，且．

（1）求的最小值；

（2）若成立，证明：或．

【答案】（1）；（2）见详解．

【解析】（1）由于

，

故由已知得，

当且仅当x=，y=–，时等号成立．

所以的最小值为．

（2）由于

，

故由已知，

当且仅当，，时等号成立．

因此的最小值为．

由题设知，解得或．

【名师点睛】两个问都是考查柯西不等式，属于柯西不等式的常见题型．

10．【2019年高考江苏卷数学】设，解不等式．

【答案】．

【解析】当x<0时，原不等式可化为，解得x<；

当0≤x≤时，原不等式可化为x+1–2x>2，即x<–1，无解；

当x>时，原不等式可化为x+2x–1>2，解得x>1．

综上，原不等式的解集为．

【名师点睛】本题主要考查解不等式等基础知识，考查运算求解和推理论证能力．