初中数学北师大版八年级上册4 一次函数的应用获奖课件ppt

这是一份初中数学北师大版八年级上册4 一次函数的应用获奖课件ppt，文件包含442《一次函数的应用》课件pptx、442《一次函数的应用》同步练习doc、442《一次函数的应用》教学设计教案doc等3份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

一次函数的应用（一）有理数
1.能运用一次函数表达式和图象之间的相互关系，处理一些复杂的问题.2.掌握根据图像得出信息的方法.3.通过练习进一步增加数形结合的意识。
教学重点： 掌握根据图像得出信息的方法。教学难点：熟练运用一次函数的知识点解决实际问题。
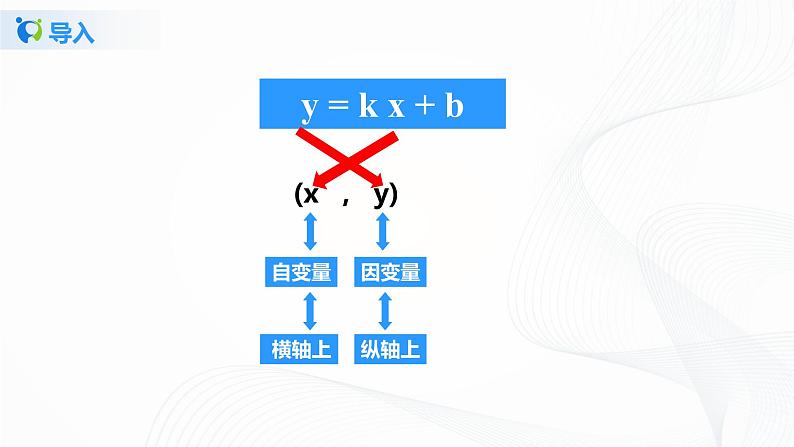
(x , y)
y = k x + b
１.设——一次函数表达式 y=kx+b或者y=kx；２.代——将点的坐标代入y=kx+b中,列出关于K、b的方程３.解——解方程求出K、b值；４.定——把求出的k、b值代回到表达式中即可.
求一次函数的表达式的详细步骤
解答实际情景函数图象信息问题的方法：
一次函数y=kx+b(k、b是常数，k≠0) 的图像和性质
(0,b)(1,k+b)
如图，l1反映了某公司产品的销售收入与销售量的关系，l2反映了该公司产品的销售成本与销售量的关系，根据图象填空：(1)当销售量为2t时，销售收入=_____元， 销售成本=____元；(2)当销售量为6t时，销售收入=_____元， 销售成本=____元；(3)当销售量等于___时，销售收入等于 销售成本；(4)当销售量____时，该公司盈利（收入大于成本）； 当销售量_____时，该公司亏损（收入小于成本）；(5) l1对应的函数表达式是_____,l2对应的函数表达式是_____.
图中，l1对应的一次函数y=k1x+b1中，k1和b1的实 际意义各是什么？l2对应的一次函数y=k2x+b2中， k2和b2的实际意义各是什么？答： k1的实际意义是：每销售1t产品的销售收入； b1的实际意义是：未销售时，销售收入为0； k2的实际意义是：每销售1t的销售成本； b2的实际意义是：未销售时，为销售所花的成本为2000元.
从图表中获取信息的应用
公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台，租车费用为400元，每辆乙种货车一次最多运送机器30台，租车费用为280元．
(1)设租用甲种货车x辆(x为非负整数)，试填写表格． 表一：
－280x＋2 240
能完成此项运送任务的最节省费用的租车方案是甲种货车6辆，乙种货车2辆．理由：当租用甲种货车x辆时，设两种货车的总费用为y元，则两种货车的总费用y＝400x＋(－280x＋2 240)＝120x＋2 240.
(2)给出能完成此项运送任务的最节省费用的租 车方案，并说明理由．
又因为45x＋(－30x＋240)≥330，所以x≥6. 因为120＞0，所以在函数y＝120x＋2 240中，y随x的增大而增大．所以当x＝6时，y取得最小值．即能完成此项运送任务的最节省费用的租车方案是甲种货车6辆，乙种货车2辆．
此题主要考查了用待定系数法求一次函数的关系式及函数图象与x轴交点坐标的求法，根据图象得出正确的信息是解题关键．
手机上网已经成为当今年轻人时尚的网络生 活，某网络公司看中了这种商机，推出了两种手机上网的 计费方式：方式A以每分钟0.1元的价格按上网时间计费； 方式B除收月租费20元外，再以每分钟0.06元的价格按上 网时间计费．假设某客户月上网时间为x min，上网费用 为y元． (1) 分别写出该客户按A，B两种方式的上网费用 y(元)与每月上网时间x(min)的函数关系式， 并在图所示的坐标系中画出这两个函数的图象； (2) 如何选择计费方式能使该客户上网费用更合算？
导引： (1) 根据题意可直接写出A，B两种上网方式的上网费用 y(元)与每月上网时间x(min)的函数关系式，再分别取x的 一些特殊值，如0，500，算出对应的y值，根据一次函数 的图象是一条直线，分别过求得的两点画直线即可画出 这两个函数的图象；(2)根据题意并观察图象可得到不同 上网时间范围内选择何种计费方式上网更合算． 解： (1)设方式A：yA＝k1x，方式B：yB＝k2x＋b. 由题意易求得yA＝0.1x，yB＝0.06x＋20， 当x＝0时，yA＝0，yB＝20；
当x＝500时，yA＝50，yB＝50，所以一次函数yA＝0.1x的图象过点 (0，0)， (500，50)，一次函数yB＝ 0.06x＋20的图象过点(0，20)，(500， 50)，其图象如图所示．(2)通过观察图象可知，当每月上网时 间少于500 min时，选择方式A更合算；当每月上网时间为500 min时，两种上网方式 所需费用相同；当每月上网时间多于 500 min时，选择方式B更合算．
利用一次函数的图象解决实际问题这类题是近几年中考中的热点问题．运用一次函数的知识判断何种方式更合算时，常通过观察函数图象得到．
我边防局接到情报，近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶（如图).图中l1，l2分别表示两船相对于海岸的距离s (n mile )与追赶时间t（min)之间的关系. 根据图象 回答下列问题：
（1）哪条线表示B到海岸的距离与追赶时间之间的关系？（2）A, B哪个速度快？（3）15min内B能否追上A?（4）如果一直追下去，那么B能否追上A?（5）当A逃到离海岸12 n mile的公海时，B将无法对其进行检查.照此速度，B能否在A逃入公海前将其拦截？（6）l1与l2对应的两个一次函数s = k1t+b1与s = k2t+b2中，k1，k2的实际意义各是什么？可疑船只A与快艇B的速度各是多少?
解：（1）当t= 0时，B距海岸0nmile，即s = 0,故l1表示B 到海岸的距离与追赶时间之间的关系. （2）t从0增加到10时，l2的纵坐标增加了 2，而l1的纵 坐标增加了 5, 即10min内，A行驶了 2nmile，B 行驶了5nmile，所以B的速度快. （3）延长l1,l2(如图)，可以看出， 当t= 15时，l1上的对应点在 l2上对应点的下方，这表明， 15 min时B尚未追上A.
（4）如图，l1，l2相交于点P.因此，如果一直追下去， 那么B一定能 追上A.（5）图中，l1与l2交点P的纵坐标小于12,这说明， 在A逃入公海前， B能够追上A.（6）k1表示快艇B的速度， k2表示可疑船只A的速度.可疑船只A的速 度是0.2 n mile/min， 快艇B的速度是0.5 n mile/min.
2.有同学画了下面一条直线的图象，你知道该函数的表达式吗？
1.若一次函数 y = 2x + b的图象经过点A(-1，4），则 b=＿＿；该函数图象经过点B(1，＿）和点C（___，0）.
3. 已知直线 y=2x－4 （1）求直线关于x轴对称的函数关系式
(3)求直线绕原点旋转1800时的函数关系式
(2)求直线关于y轴对称的函数关系式
y= － 2x- 4
4.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( ) (A) (B) （C） （D）
5、某汽车行驶时间t(时)与该汽车对于某城市的距离y(千米)之间的关系式为 (t≥0)，其图象如图所示：(1)在1时至3时之间，汽车行驶的路程是多少？(2)你能确定k的值吗？这里k的具体含义是什么？
解：（1）当t=1时，y=90;当t=3时，y=_____；
所以，在1时至3时之间，汽车行驶的路程是______千米
（2）把t=1，y=90代人得K=60，K表示汽车行驶的速度。
从函数图象得到需要的信息，再求出函数表达式从而解决实际问题和几何问题，是一次函数应用价值的体现，这种题型常与一些热点问题结合，考查学生综合分析问题、解决问题的能力．
教材95页习题第1、2题。