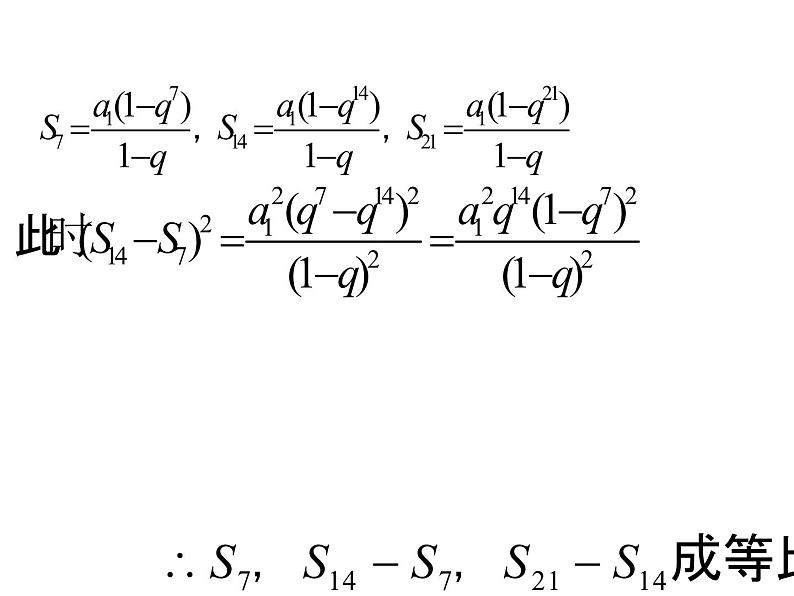
高中数学苏教版 (2019)选择性必修第一册4.1 数列评课ppt课件

这是一份高中数学苏教版 (2019)选择性必修第一册4.1 数列评课ppt课件，共32页。PPT课件主要包含了但是这是有前提的，数列求和，知识梳理，分析数列通项，选择求和方法，基本数列求和，分组法求和，分析通项，变式训练3，例2求和等内容，欢迎下载使用。
这数列里面的任何一项都不能为0！
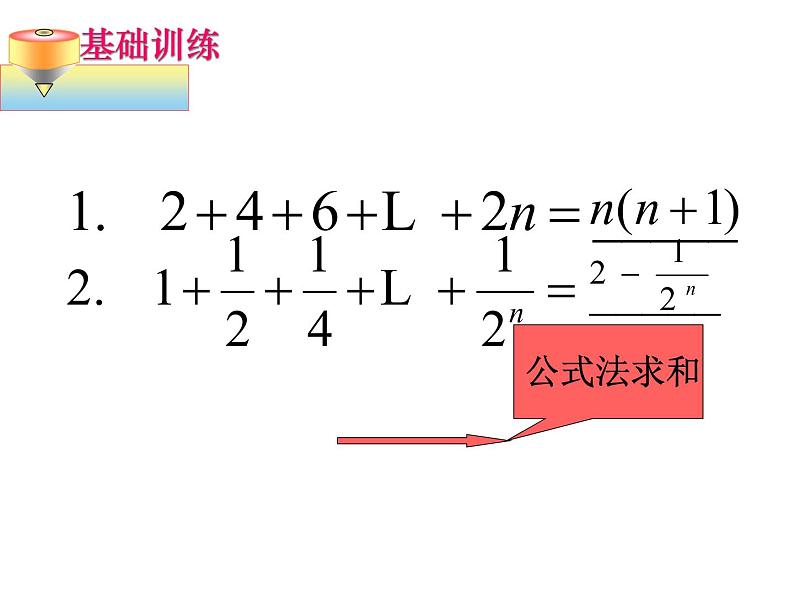
1.等差数列前n项和:
2.等比数列前n项和:
公式法求和的前提是由已知条件能得到此数列是等差或等比数列，因此，要求不仅要牢记公式，还要计算准确无误。
在什么情况下，用公式法求和？
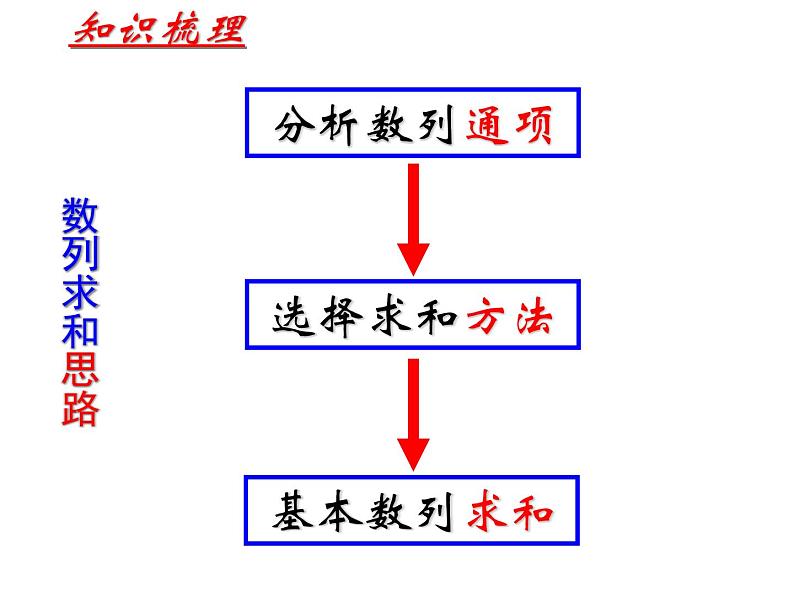
求前n项和关键的第一步：
在什么情况下，用分组求和？
合 并 求 和 法
当n为偶数时，设n=2k，则
例3、已知{ }的前n项和 ， 求 的前n项和 。
分析：此数列为特殊数列，其通项的 分母是两个因式之积，且两数 相差1
若把通项作适当变形为
把数列的通项拆成两项之差 ，在求和时中间的一些项可以相互抵消，从而求得其和 ；
的值为 。
例6.求数列 前n项的和
如果一个数列的各项是由一个等差数列与一个等比数列对应项乘积组成，此时求和可采用错位相减法.
{ }的通项是等差数列{2n}的通项与等比数列{ }的通项之积
例6.求数列 前n项的和.
在什么情况下，用错位相减法求和？
变式、求和Sn =1+2x+3x2+……+nxn-1
这是一个等差数列{n}与一个等比数列{xn-1}的对应相乘构成的新数列，这样的数列求和该如何求呢？
Sn =1 + 2x +3x2 + …… +nxn-1 ①
xSn = x + 2x2 +……+ (n-1)xn-1 + nxn ②
(1-x)Sn =1 +（x + x2+ …… + xn-1 ） - nxn
这时等式的右边是一个等比数列的前n项和与一个式子的和，这样我们就可以化简求值。
变式、求和Sn =1+2x+3x2+ +nxn-1 (x≠0,1)
解：∵ Sn =1 + 2x +3x2 + +nxn-1
∴xSn = x + 2x2 + + (n-1)xn-1+nxn
∴ ① -②，得：(1-x) Sn =1+（x+x2+ + xn-1 )- nxn
直接利用等差等比数列的求和公式
有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.
把数列的通项拆成两项之差，即数列的每一项都可按此法拆成两项之差，在求和时一些正负项相互抵消，于是前n项的和变成首尾若干少数项之和，这一求和方法称为裂项相消法.
如果一个数列的各项是由一个等差数列与一个等比数列对应项乘积组成，此时求和可采用错位相减法.