2020-2021学年3.2函数关系的建立教学设计及反思

这是一份2020-2021学年3.2函数关系的建立教学设计及反思，共16页。
知识梳理与应用
易错一：解析式中的定义域
（1）分母不为零：；
（2）偶次根式的被开方数非负：；
（3）对数中，底数大于且不为，真数部分大于0：
；
（4）0次幂与负次幂底数不为0：；
【例1】（2020·上海市第二中学高一月考）★★☆☆☆
求下列函数的定义域.
（1）；
（2）；
（3）.
【答案】（1）；（2）；
（3）.
【详解】
解：（1）因为，所以，解得且，所以函数的定义域为：；
（2）因为，所以解得且，故函数的定义域为；
（3）
解得：或
所以函数的定义域为；
故答案为：.
【练习】（2021·上海交大附中高一开学考试）★★☆☆☆
函数的定义域为__________．
【答案】
【详解】
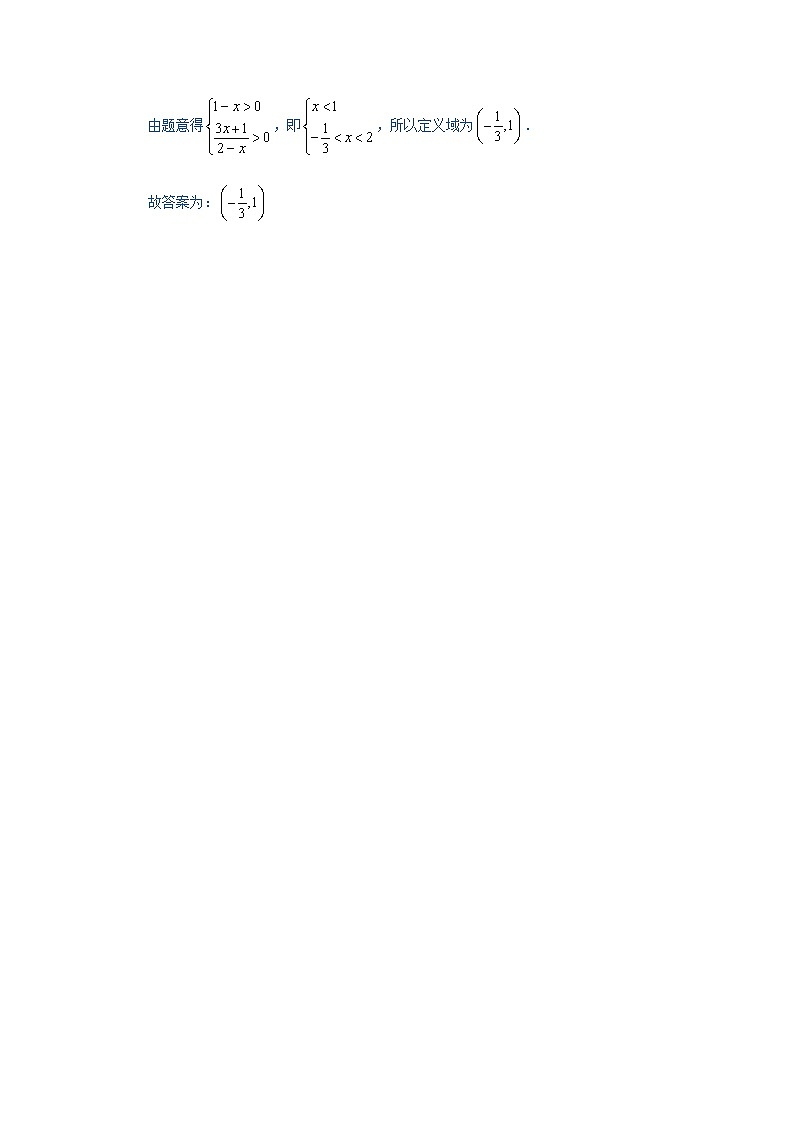
由题意得，即，所以定义域为．
故答案为：
易错二：函数运算的定义域
设定义域分别为，则函数的定义域均为.
【例2】（2020·上海市控江中学）★★☆☆☆
设函数，，则函数的定义域为__________.
【答案】
【详解】
定义域均满足，解，
所以的定义域为.
故答案为:.
【练习】（2016·上海市建平中学高一期末）★★☆☆☆
函数，，则________．
【答案】
【详解】
解：，，
，
故答案为：，．
易错三：复合函数的定义域
设定义域分别为，则函数的定义域为.
【例3】（2021·上海浦东新区·华师大二附中高一月考）★★☆☆☆
已知函数的定义域为，则函数的定义域为___________.
【答案】
【详解】
函数的定义域为，
则函数中，解得，
故答案为：.
【例4】（2015·上海高三月考）★★☆☆☆
已知函数的定义域是，求函数的定义域是______.
【答案】
【详解】
解：函数的定义域是，
，
，
函数的定义域是；
故答案为：．
【例5】（2018·上海市七宝中学高三月考）★★★☆☆
已知的定义域为，则的定义域为________.
【答案】
【详解】
由于中，∴，
∴中：，∴.
故答案为.

【练习】（编者精选）★★★☆☆
已知的定义域为[－1，1]，则的定义域是_________．
【答案】．
【详解】
试题分析：∵的定义域为[－1，1]，∴，令，∴，
即的定义域是．
易错四：题设中的定义域
很多题目，并不是根据解析式来确定定义域，而是在题干中就已经规定了函数的定义域，在做题时一定要看清题目，不要根据解析式上来就下笔.
【例6】（2016嘉定区三模改）★★★★☆
（2016嘉定区三模改）已知函数是定义在上的函数，其图像关于原点对称，且当时，，若，则实数的取值范围是_________________.
【答案】
【详解】
当时，，严格递增；
作出函数的图象大致如下图所示：
由图象可知，函数在上严格递增，
，解得.
因此，实数的取值范围是.
【例7】（2017·上海市南洋模范中学高二开学考试）★★★★☆
定义在的函数严格递增，且对任意的，，.
（1）求；
（2）若，求的取值范围.
【答案】（1）；（2）.
【详解】
（1）令；
（2）由（1）得，不等式
变形为，在是增函数，
不等式等价于，解得.
所以的取值范围是.
【练习】（2021·上海市行知中学高一月考改）★★★☆☆
定义在上的函数的图像关于轴对称，且在上是下降的，由，则的取值范围是______.
【答案】
【详解】
可类比二次函数，根据图像有
又因为，所以，解得，
所以的取值范围是，故答案为：.
易错五：实际问题中的限制条件
在实际问题中，有些变量具有实际意义，其取值范围往往要受到其实际意义的制约，例如人数是自然数，时间是正数等.
【例8】（2021·上海市建平中学高三三模）★★★☆☆
上海市某地铁项目正在紧张建设中，通车后将给更多市民出行带来便利，已知该线路通车后，地铁的发车时间间隔t（单位：分钟）满足，，经测算，在某一时段，地铁载客量与发车时间间隔t相关，当时地铁可达到满载状态，载客量为1200人，当时，载客量会减少，减少的人数与的平方成正比，且发车时间间隔为2分钟时载客量为560人，记地铁载客量为.
（1）求的解析式；
（2）若该时段这条线路每分钟的净收益为（元），问当发车时间间隔为多少时，该时段这条线路每分钟的净收益最大？
【答案】（1）；（2）分钟.
【详解】
（1）由题意知，（k为常数），
因，则，
所以；
（2）由得，
即，
①当时，，当且仅当等号成立；
②当时，在[10，20]上递减，当时Q取最大值24，
由①②可知，当发车时间间隔为分钟时，该时段这条线路每分钟的净收益最大，最大为120元.
【练习】（2017·上海曹杨二中高一期中）★★★☆☆
用长为的铁丝完成下部为矩形，上部为半圆形的框架，若半圆半径为，求此框架围城的面积关于的函数关系式，并写出它的定义域.
【答案】；定义域为
【详解】
如图：由题意，半圆半径为，则，弧长

，
，
由，解得，
故函数的定义域为.
1、（2020·上海市进才中学高三期中）★★☆☆☆
函数的定义域是______.
【答案】[-1，2]
【详解】
由题设可得即，
故，所以，
故答案为：.
2、（2017·上海市七宝中学高一期中）★★☆☆☆
设函数.则函数________.
【答案】
【详解】
先求出两个函数的定义域，
的定义域为；
的定义域为，
的定义域为，，，且，
故答案为：，，，．
3、（2017·上海大学市北附属中学高一期中）★★☆☆☆
函数的定义域，则函数的定义域为__________.
【答案】
【详解】
∵函数的定义域为，，
∴，解得，
∴函数的定义域为.
故答案为：.
4、（2018·上海市比乐中学高一期中）★★☆☆☆
若等腰三角形的周长为，将腰长表示成底边长的函数（需注明定义域）_______.
【答案】
【详解】
因为等腰三角形的周长，所以，根据三角形任意两边之和大于第三边可知，所以函数解析式为.
故答案为