2020-2021年山东省青岛市高二（上）期末考试数学试卷人教A版

这是一份2020-2021年山东省青岛市高二（上）期末考试数学试卷人教A版，共15页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。

1. 若直线l1：3x−4y−1=0与l2：3x−ay+2=0a∈R平行，则l1与l2间的距离是( )
A.15B.25C.35D.45

2. 数列−1n3n−1的前2021项和为( )
A.3034B.−3034C.−3032D.3032

3. 已知相距1400m的A，B两个哨所，听到炮弹爆炸声的时间相差3s，已知声速是340m/s，则炮弹爆炸点在( )上.
A.圆B.椭圆C.抛物线D.双曲线

4. 已知数列an的前n项和为Sn，an=n−5，n∈N∗，则Sn的最小值为( )
A.S3B.S5C.S9D.S2020

5. 已知曲线mx2+2y2=1表示焦点在y轴的椭圆，则实数m的取值范围是( )
A.00的焦点恰为圆C:x2+y−12=r2r>0的圆心，抛物线E的准线与圆C相切，则下列结论正确的是( )
A.抛物线E的标准方程为x2=4y
B.圆C的标准方程为x2+y−12=4
C.圆C与抛物线E有三个交点
D.圆C与抛物线E在第一象限的交点坐标为2,1

数列an满足：a1=1, an+1−3an−1=0，n∈N∗，下列说法正确的是( )
A.数列an+12为等比数列B.an=12×3n−12
C.数列an是递减数列D.an的前n项和Sn=14×3n+1−54

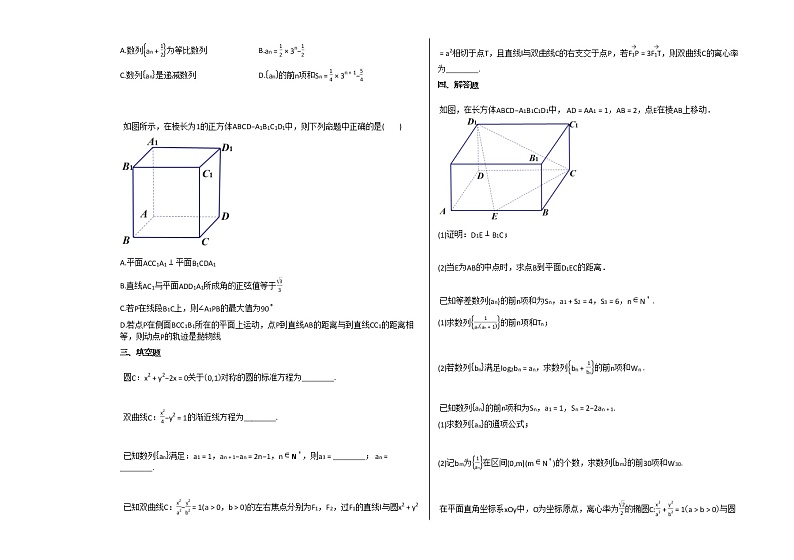
如图所示，在棱长为1的正方体ABCD−A1B1C1D1中，则下列命题中正确的是( )

A.平面ACC1A1⊥平面B1CDA1
B.直线AC1与平面ADD1A1所成角的正弦值等于33
C.若P在线段B1C上，则∠A1PB的最大值为90∘
D.若点P在侧面BCC1B1所在的平面上运动，点P到直线AB的距离与到直线CC1的距离相等，则动点P的轨迹是抛物线
三、填空题

圆C：x2+y2−2x=0关于0,1对称的圆的标准方程为________.

双曲线C：x24−y2=1的渐近线方程为________.

已知数列an满足：a1=1，an+1−an=2n−1，n∈N∗，则a3=________； an=________.

已知双曲线C：x2a2−y2b2=1(a>0，b>0)的左右焦点分别为F1，F2，过F1的直线l与圆x2+y2=a2相切于点T，且直线l与双曲线C的右支交于点P，若F1P→=3F1T→，则双曲线C的离心率为________.
四、解答题

如图，在长方体ABCD−A1B1C1D1中， AD=AA1=1，AB=2，点E在棱AB上移动．

(1)证明：D1E⊥B1C；

(2)当E为AB的中点时，求点B到平面D1EC的距离．

已知等差数列{an}的前n项和为Sn，a1+S2=4，S3=6，n∈N∗ .
(1)求数列1anan+1的前n项和Tn；

(2)若数列bn满足lg2bn=an，求数列bn+1bn的前n项和Wn .

已知数列an的前n项和为Sn，a1=1，Sn=2−2an+1.
(1)求数列an的通项公式；

(2)记bm为1an在区间(0,m](m∈N∗)的个数，求数列bm的前30项和W30.

在平面直角坐标系xOy中，O为坐标原点，离心率为22的椭圆C:x2a2+y2b2=1a>b>0与圆x2+y−122=14只有一个公共点，抛物线D:x2=−2py01m>0，
解得m>2.
故选B．
6.
【答案】
A
【考点】
等差数列的通项公式
【解析】
首先判断出数列{2n+1}与{3n}项的特征，从而判断出两个数列公共项所构成新数列的首项以及公差，利用等差数列的求和公式求得结果．
【解答】
解：因为数列{2n+1}是以3为首项，以2为公差的等差数列，
数列{3n}是以3首项，以3为公差的等差数列，
所以这两个数列的公共项所构成的新数列{an}是以3为首项，以6为公差的等差数列，
所以{an}的通项公式为an=3+6n−1=6n−3，
令6n−3=2019，
解得n=337.
故选A.
7.
【答案】
D
【考点】
抛物线的标准方程
【解析】
利用直线与抛物线的关系求解即可.
【解答】
解：由题可得示意图如图，
∵OA→⋅OB→=0，
∴|OA→|⋅|OB→|⋅cs∠AOB=0，
∴∠AOB=90∘.
∵|AB|=4 且AB⊥x，
∴AD=BD=2，
∴∠AOD=∠BOD=45∘，
∴A2,2.
将A2,2其代入y2=2px，即4=4p，
解得p=1.
故选D.
8.
【答案】
A
【考点】
用空间向量求直线与平面的夹角
【解析】
由题可知，平面α的一个法向量m→和直线l的一个方向向量n→，设直线1与平面α所成角为θ，由sinθ=|cs|=||m→|⋅|n→|˙|，即可得解．
【解答】
解：∵ 平面α的方程为3x−5y+z−7=0，
∴ 平面α的一个法向量为m→=(3, −5, 1).
∵ 经过(0, 0, 0)直线l的方程为x3=y2=z−1，
∴ 直线l的一个方向向量为n→=(3, 2, −1).
设直线l与平面α所成角为θ，
则sinθ=|cs|=|m→⋅n→||m→|⋅|n→|
=|3×3−5×2−1×132+(−5)2+12×32+22+(−1)2|
=1035，
∴ 直线l与平面α所成角的正弦值为1035．
故选A.
二、多选题
【答案】
B,C,D
【考点】
空间中直线与平面之间的位置关系
命题的真假判断与应用
平面的法向量
直线与平面所成的角
【解析】
根据直线的方向向量与平面的法向量之间的关系，逐一判断线面、面面关系即可得结论．
【解答】
解：A，若a→⊥n→，则直线a与平面α平行或在平面α内，是假命题；
B，若a→//n→，则a→也是平面α的法向量，所以直线a⊥平面α，是真命题；
C，直线与平面的夹角的正弦值等于直线与平面法向量所成的锐角的余弦值，是真命题；
D，两个平面的夹角与它们的法向量所成的不大于90∘的角相等，是真命题.
故选BCD.
【答案】
A,B,D
【考点】
抛物线的性质
圆的标准方程
圆与圆锥曲线的综合问题
【解析】
利用抛物线的相关性质求圆的标准方程，进而求解圆与抛物线的相关问题.
【解答】
解：A，∵抛物线E: x2=2py p>0 ，
∴焦点(0,p2)，准线y=−p2.
∵圆x2+(y−1)2=r2的圆心0,1，
∴p2=1，
∴ p=2，
∴E:x2=4y，故A正确；
B，∵E的准线方程为y=−1，其准线与圆相切，
∴圆心到准线的距离为r=1−−1=2，
∴圆的方程为x2+(y−1)2=4，故B正确；
C，联立x2=4y，x2+(y−1)2=4得y2+2y−3=0，
解得y=1或y=−3（不符合题意，舍去），
∴ 当y=1时，x=±2，
∴圆与抛物线有2个交点，故C错误；
D，在第一象限交点坐标为(2,1)， 故D正确.
故选ABD.
【答案】
A,B
【考点】
等比数列的性质
等比数列的通项公式
等比数列的前n项和
等比关系的确定
【解析】
利用递推公式变形求解，逐项判定即可.
【解答】
解：A， ∵an+1−3an−1=0，
∴an+1+12=3an+12，
即an+1+12an+12=3，
∴ 数列an+12为以首项为32，公比为3的等比数列，A正确；
B，由A得an+12=32×3n−1，
∴an =12×3n−12 ，B正确 ；
C，∵an =12×3n−12 ，
∴数列an是递增数列，C错误；
D，Sn=12×31−3n1−3−12n
=−14×3n+1−34−n2 ，D错误.
故选AB.
【答案】
B,D
【考点】
直线与平面所成的角
异面直线及其所成的角
平面与平面垂直的判定
轨迹方程
余弦定理
【解析】
利用空间向量判断平面与平面垂直、直线与平面的夹角，求动点的轨迹.
【解答】
解：以A为原点，AB→为x轴，AD→为y轴，AA1→为z轴，建立如图所示的空间直角坐标系.
则A0,0,0，B1,0,0，C1,1,0，D0,1,0
A10,0,1，B11,0,1，C11,1,1，D10,1,1,
∴ AA1→=0,0,1，AC→=(1,1,0)，
设平面ACC1A1的法向量为m→=(x1,y1,z1)，
则AA1→⋅m→=0，AC→⋅m→=0，
即z1=0，x1+y1=0，
令x1=1，y1=−1，
∴ m→=(1,−1,0).
A1B1→=(1,0,0)，B1C→=(0,1,−1)，
设平面B1CDA1法向量为n→=(x2,y2,z2)，
则A1B1→⋅n→=0，B1C→⋅n→=0，
即x2=0，y2−z2=0，
令y2=1，z2=1，
∴ n→=(0,1,1)，
∴m→⋅n→=−1≠0 ，故A错误；
∵ C1D1⊥平面ADD1A1，
∴∠C1AD1即为直线AC1与平面ADD1A1所成的角.
∵ C1D⊥AD1，C1D1=1，AC1=3，
sin∠C1AD1=13=33，故B正确 ；
P在B1C上，设P1,x,1−x0≤x≤1，
A1P2+BP2−A1B2
=1+2x2+1+2x2−2x−2
=4x2−2x，
当0