2020-2021学年山东省青岛市高二（上）10月月考数学试卷 (2)人教A版（2019）

这是一份2020-2021学年山东省青岛市高二（上）10月月考数学试卷 (2)人教A版（2019），共17页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。

1. 若直线l1：y=2x+1与l2：3m+1x−2y+5=0平行，则m=( )
A.1B.−1C.2D.−2

2. 过A2,6，B1,−6两点的直线的斜率为( )
A.−12B.−112C.112D.12

3. 已知△ABC三个顶点的坐标分别为A2,6，B1,−6，C(5,2)，M为BC的中点，则中线AM所在直线的方程为( )
A.10x+y−26=0B.8x+y−22=0C.8x+y−26=0D.10x−y−34=0

4. 在长方体ABCD−A1B1C1D1中，设AB→=a→，AD→=b→，AA→1=c→，且|a→|=2，则a→+b→⋅a→−c→=( )
A.1B.2C.3D.4

5. 直四棱柱ABCD−A1B1C1D1的各棱长均为2，且∠BAD=π3，则|AC1→|=( )
A.23B.10C.4D.33

6. 如图，在正方体ABCD−A1B1C1D1中，AB=4，若点P在侧面BCC1B1（不含边界）内运动，AP⊥BD1，且点P到底面ABCD的距离为3，则异面直线BD与AP所成角的余弦值是( )

A.1326B.1313C.31313D.31326

7. 已知P，A，B，C四点满足PA→=1,1,−3，PB→=2,−1,1，PC→=3,4,m，且P，A，B，C四点共面，则m=( )
A.113B.−13C.−343D.343

8. 已知在四面体ABCD中，AB=CD=10，AC=BD=13，AD=BC=5，M为棱AB的中点，DN→=13DC→，连接MN，则点A到MN所在直线的距离的平方为( )

A.6977B.369154C.1011D.6577
二、多选题

以下关于向量的说法中正确的是( )
A.若将所有空间单位向量的起点放在同一点，则终点围成一个圆
B.若a→=b→，则|a→|=|b→|
C.若a→与b→共线，b→与c→共线，则a→与c→共线
D.若a→=−b→且b→=−c→，则a→=c→

在四面体ABCD中，E，F分别是BC，BD上的点，且BEEC=BFFD=2，则EF→−AC→+AD→=( )
A.52EF→B.43EF→C.89CD→D.53CD→

已知直线l与函数y=lg2x的图象有两个交点Pa,b，Qc,d，且PQ的中点在x轴上，则下列说法正确的是( )
A.l的斜率大于0B.ac=1
C.a+c=1D.l在x轴的截距大于1

在三棱锥P−ABC中，以下说法正确的有( )
A.若2AD→=AB→+AP→，则BP→=3BD→
B.若PA→⋅AC→=0，PA→⋅AB→=0，则PA→⋅BC→=0
C.若PA=PB=PC=2，AB=AC=BC=22，M，N分别为PA，BC的中点，则|MN→|=2
D.若T为△ABC的重心，则2PT→+AT→=PB→+PC→
三、填空题

已知直线l的方向向量m→=1,−2,3，平面α的法向量n→=t,t+1,−1，若l//α，则t=________.

已知直线l:x2+y6=1与x轴和y轴分别交于A，B两点，O为坐标原点，则△AOB的面积为________.

设A1,1，B3,5，C5,3，D0,−7，E2,−3，F8,−6，若直线l分别与△ABC及△DEF各恰有一个交点，则直线l的斜率的最小值为________.

如图，已知四棱柱ABCD−A1B1C1D1的底面A1B1C1D1为平行四边形，E为棱AB的中点，AF→=13AD→，AG→=2GA1→，AC1与平面EFG交于点M，则AMAC1=________.

四、解答题

在①它的倾斜角比直线y=3x−1的倾斜角小π12，②与直线x+y−1=0垂直，③在y轴上的截距为−1，这三个条件中任选一个，补充在下面的问题中，并作答．问题：已知直线l过点2,1，且________，求直线l的方程．
注：如果选择多个条件分别解答，按第一个解答计分．

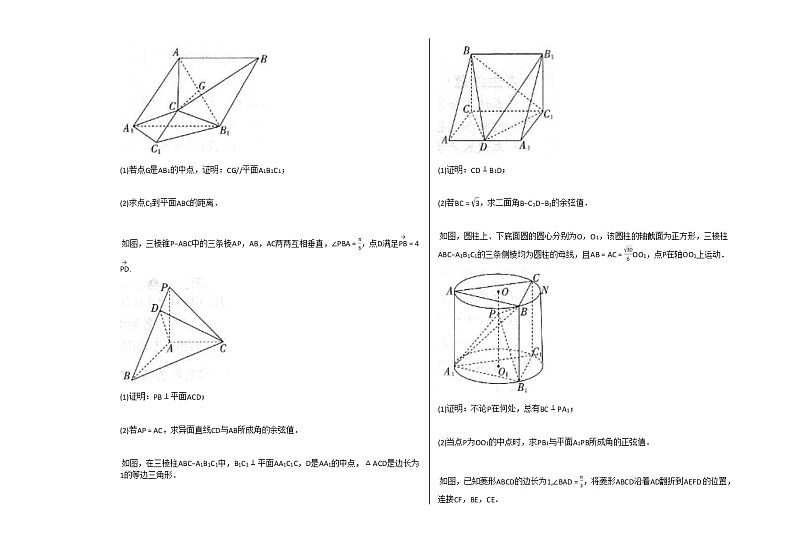
如图，在多面体ABC−A1B1C1中，平面AA1B1B⊥平面A1B1C1，四边形AA1B1B是菱形，AA1//CC1，AA1=2CC1=4，∠AA1B1=60∘.C1A1=C1B1=5.

(1)若点G是AB1的中点，证明：CG//平面A1B1C1；

(2)求点C1到平面ABC的距离．

如图，三棱锥P−ABC中的三条棱AP，AB，AC两两互相垂直，∠PBA=π6，点D满足PB→=4PD→.

(1)证明：PB⊥平面ACD；

(2)若AP=AC，求异面直线CD与AB所成角的余弦值．

如图，在三棱柱ABC−A1B1C1中，B1C1⊥平面AA1C1C，D是AA1的中点，△ACD是边长为1的等边三角形．

(1)证明：CD⊥B1D；

(2)若BC=3，求二面角B−C1D−B1的余弦值．

如图，圆柱上、下底面圆的圆心分别为O，O1，该圆柱的轴截面为正方形，三棱柱ABC−A1B1C1的三条侧棱均为圆柱的母线，且AB=AC=306OO1，点P在轴OO1上运动．

(1)证明：不论P在何处，总有BC⊥PA1；

(2)当点P为OO1的中点时，求PB1与平面A1PB所成角的正弦值．

如图，已知菱形ABCD的边长为1,∠BAD=π3，将菱形ABCD沿着AD翻折到AEFD 的位置，连接CF，BE，CE．

(1)证明：BE//平面FCD．

(2)在翻折的过程中，能否使得BE与平面ECD所成的角的正弦值为21313？若能，求出二面角B−AD−E的大小；若不能，请说明理由．
参考答案与试题解析
2020-2021学年山东省青岛市高二（上）10月月考数学试卷
一、选择题
1.
【答案】
A
【考点】
两条直线平行与倾斜角、斜率的关系
【解析】
无
【解答】
解：根据题意得，3m+12=2，
解得m=1．
故选A．
2.
【答案】
D
【考点】
斜率的计算公式
【解析】

【解答】
解：斜率k=6−(−6)2−1=12.
故选D.
3.
【答案】
B
【考点】
直线的一般式方程
直线的两点式方程
中点坐标公式
【解析】
无
【解答】
解：由中点坐标公式得M3,−2，
所以kAM=−8，
所以AM的方程为y+2=−8x−3，
即8x+y−22=0．
故选B．
4.
【答案】
D
【考点】
空间向量的数量积运算
【解析】
无
【解答】
解：在长方体中，a→⋅b→=b→⋅c→=c→⋅a→=0，
所以a→+b→⋅a→−c→
=a→2+a→⋅b→−a→⋅c→−b→⋅c→=22+0−0−0=4．
故选D．
5.
【答案】
C
【考点】
空间向量的数乘运算
向量的模
【解析】
无
【解答】
解：AC1→=AB→+AD→+AA1→，
又有∠BAD=π3，且各棱长均为2，
所以AB→⋅AD→=2×2×12=2，AA1→⋅AB→=0，AA1→⋅AD→=0，
所以AC1→2=AB→2+AD→2+AA1→2+2AB→⋅AD→+2AA1→⋅AB→+2AA1→⋅AD→
=4+4+4+4=16，
从而|AC1→|=4．
故选C．
6.
【答案】
D
【考点】
用空间向量求直线间的夹角、距离
【解析】

【解答】
解：以D为坐标原点建立如图所示的空间直角坐标系D−xyz，
则A4,0,0，B4,4,0，D0,0,0，D10,0,4,
由条件设Px,4,3，00)，则AB=AC=306a．
在△ABC中，AM=AC⋅cs∠CAM=AC×ACAN=56a,
则OM=13a．
从而CM=BM=306a2−56a2=56a，
则A10,−12a,0 ，B56a,13a,a，P0,0,12a，B156a,13a,0，
可得A1P→=0,12a，12a,A1B→=56a,56a,a．
设平面A1PB的一个法向量为n→=x,y,z，
则有12ay+12az=0,56ax+56ay+az=0,
取x=1，得n→=1,5,−5，
又因为PB1→=56a,13a,−12a，
设PB1与平面A1PB所成角为θ，
则 sinθ=|cs⟨n→,PB1→⟩|=5a1+5+5⋅536a2+19a2+14a2=11011 .
即PB1与平面A1PB所成角的正弦值为11011．
【答案】
(1)证明：由已知，AB//CD，AE//DF, AB∩AE=A, DC∩DF=D,
所以平面ABE//平面FCD.
因为BE⊆平面ABE，
所以BE//平面FCD．
(2)解：取AD的中点O，连接OE，OB，BD.
由∠BAD=π3，得△ADE，△ADB都是等边三角形，且边长为1，
所以OE⊥AD，OB⊥AD，
所以AD⊥平面BOE，
所以∠BOE是二面角B−AD−E的平面角．
设∠BOE=θ．
在平面BOE中过点O作Oz⊥OB，则Oz⊥平面ABCD．
即Oz⊥OA，Oz⊥OB，
以O为原点，OA→，OB→，Oz→的方向分别为x，y，z轴的正方向，建立空间直角坐标系O−xyz．
如图所示，
则B0,32,0，E0,32csθ,32sinθ，C−1,32,0，D−12,0,0，
所以BE→=0,32csθ−32,32sinθ，DE→=12,32csθ,32sinθ，DC→=−12,32,0.
设平面CDE的法向量为n→=x,y,z，
则n→⋅DE→=0，n→⋅DC→=0，
12x+32ycsθ+32zsinθ=0，−12x+32y=0，
令 x=3，则y=1，z=1+csθ−sinθ，
于是n→=3,1,−1+csθsinθ．
设BE与平面ECD所成的角为α，则
sin α=|cs|
=34+(1+csθ)2sin2θ⋅32(1−csθ)
=21313，
解得θ=2π3.
故能使BE与平面ECD所成角的正弦值为21313，此时二面角B−AD−E的大小为2π3.
【考点】
用空间向量求平面间的夹角
直线与平面平行的判定
【解析】


【解答】
(1)证明：由已知，AB//CD，AE//DF, AB∩AE=A, DC∩DF=D,
所以平面ABE//平面FCD.
因为BE⊆平面ABE，
所以BE//平面FCD．
(2)解：取AD的中点O，连接OE，OB，BD.
由∠BAD=π3，得△ADE，△ADB都是等边三角形，且边长为1，
所以OE⊥AD，OB⊥AD，
所以AD⊥平面BOE，
所以∠BOE是二面角B−AD−E的平面角．
设∠BOE=θ．
在平面BOE中过点O作Oz⊥OB，则Oz⊥平面ABCD．
即Oz⊥OA，Oz⊥OB，
以O为原点，OA→，OB→，Oz→的方向分别为x，y，z轴的正方向，建立空间直角坐标系O−xyz．
如图所示，
则B0,32,0，E0,32csθ,32sinθ，C−1,32,0，D−12,0,0，
所以BE→=0,32csθ−32,32sinθ，DE→=12,32csθ,32sinθ，DC→=−12,32,0.
设平面CDE的法向量为n→=x,y,z，
则n→⋅DE→=0，n→⋅DC→=0，
12x+32ycsθ+32zsinθ=0，−12x+32y=0，
令 x=3，则y=1，z=1+csθ−sinθ，
于是n→=3,1,−1+csθsinθ．
设BE与平面ECD所成的角为α，则
sin α=|cs|
=34+(1+csθ)2sin2θ⋅32(1−csθ)
=21313，
解得θ=2π3.
故能使BE与平面ECD所成角的正弦值为21313，此时二面角B−AD−E的大小为2π3.