高中数学第十一章 立体几何初步11.1 空间几何体11.1.4 棱锥与棱台教学设计

这是一份高中数学第十一章 立体几何初步11.1 空间几何体11.1.4 棱锥与棱台教学设计，共12页。教案主要包含了情境与问题，达标检测，小结，课时练等内容，欢迎下载使用。

本节《普通高中课程标准数学教科书-必修四（人教B版）第十一章《11.1.4 棱锥与棱台》， 本节课要学的内容棱锥与棱台的概念、分类及基本量的计算。引导学生通过观察生活中的实物，经历尝试与探究的过程，进行数学抽象概括，获得棱锥与棱台的相关概念。从而发展学生的逻辑推理、数学建模、数学运算和直观想象的核心素养。
1.教学重点：了解棱锥、棱台的定义和结构特征．
2.教学难点：掌握棱锥、棱台平行于底面的截面的性质．
多媒体
本课以生活中的实物为出发点，引导学生通过观察，分析、抽象概括出棱锥与棱台的概念。从而发展学生的逻辑推理、数学建模和直观想象的核心素养。教学中要注重学生的主体地位，调动学
生积极性，使数学教学成为数学活动的教学。
课程目标
学科素养
A. 了解棱锥、棱台的定义和结构特征．
B.掌握棱锥、棱台平行于底面的截面的性质．
C.掌握棱锥与棱台中的相关计算问题。
1.数学抽象：棱锥、棱台的概念；
2.逻辑推理：概念的运用；
3.数学建模：棱锥、棱台的结构；
4.直观想象：棱锥、棱台与棱柱的区别与联想；
5数学运算：棱锥、棱台的相关计算问题。
教学过程
教学设计意图
核心素养目标
一、情境与问题
1：棱锥
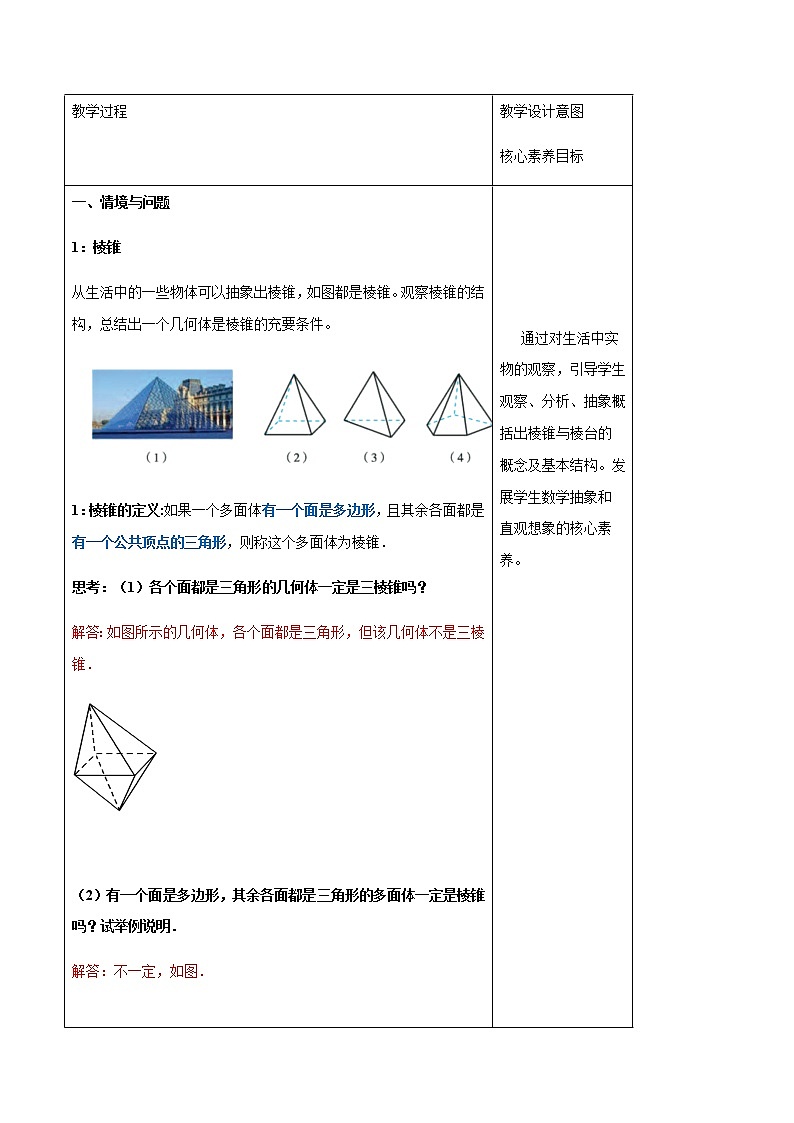
从生活中的一些物体可以抽象出棱锥，如图都是棱锥。观察棱锥的结构，总结出一个几何体是棱锥的充要条件。
1：棱锥的定义:如果一个多面体有一个面是多边形，且其余各面都是有一个公共顶点的三角形，则称这个多面体为棱锥．
思考：（1）各个面都是三角形的几何体一定是三棱锥吗？
解答：如图所示的几何体，各个面都是三角形，但该几何体不是三棱锥．

（2）有一个面是多边形，其余各面都是三角形的多面体一定是棱锥吗？试举例说明．
解答：不一定，如图．
2：棱锥的结构特征
棱锥中，是多边形的那个面称为棱锥的底面，有公共顶点的各三角形称为棱锥的侧面，
各侧面的公共顶点称为棱锥的顶点，相邻两侧面的公共边称为棱锥的侧棱．
3：棱锥的分类
按底面的形状分为三棱锥(底面是三角形)、四棱锥(底面是四边形)，五棱锥(底面是五边形)，…….
如图11-1-31，（2）是一个四棱柱、（3）是一个三棱锥、（4）是一个五棱锥.
4：棱锥的表示
棱锥可以用顶点与底面各顶点的字母来表示，例如四棱锥可表示为：四棱锥P－ABCD或四棱锥P－AC．
5：棱锥的高和侧面积
过棱锥的顶点作棱锥底面的垂线，所得到的线段(或它的长度)称为棱锥的高．
棱锥所有侧面的面积之和称为棱锥的侧面积．
如图，PO为棱锥的高，因此面ABCD
从而可知：
6：正棱锥及其性质
(1)正棱锥的定义：如果棱锥的底面是正多边形，且棱锥的顶点与底面中心的连线垂直于底面，
则称这个棱锥为正棱锥．
(2)正棱锥的性质：正棱锥的侧面都全等，而且都是等腰三角形，这些等腰三角形底边上的高也都相等，称为棱锥的斜高．
例1.如图是底面边长为1且侧棱长为的正六棱锥
（1）写出直线PA与直线CD，直线PA与面ABCDEF之间的关系；
（2）求棱锥的高和斜高；
（3）求棱锥的侧面积
解：（1）直线PA与直线CD异面，直线面ABCDEF=A
（3）因为的面积为：.故棱锥的侧面积为：
（2）作出棱锥的高PO，因为是正六棱锥，所以O是底面的中心，连接OC，可知OC=1
在中，可知： ；
设BC的中点为M，由为等腰三角形可知， ，因此PM为斜高，从而
【变式练习】已知正四棱锥的底面边长为4，高是2，则它的表面积为________.
∵AO＝2，OB＝2，∴AB＝2eq \r(2).
又∵S侧＝4×eq \f(1,2)×4×2eq \r(2)＝16eq \r(2)，
S底＝4×4＝16，∴S表＝S侧＋S底＝16＋16eq \r(2).
2：棱台
从生活中的一些物体可以抽象出棱台，如图都是棱台。观察棱台的结构，总结出一个几何体是棱台的充要条件。
1：棱台的定义
一般地，用平行于棱锥底面的平面去截棱锥，所得截面与底面间的多面体称为棱台．
原棱锥的底面与截面分别称为棱台的下底面和上底面，其余各面称为棱台的侧面，
相邻两侧面的公共边称为棱台的侧棱．
2：棱台的分类及表示
按底面的形状分为三棱台(底面是三角形)、四棱台(底面是四边形)、……，棱台可用上底面与下底面的顶点表示，
例如底面是四边形的棱台可表示为四棱台ABCD－A′B′C′D′.
如图所示的棱台 ，可以看出是从棱锥P-ABCD上截去棱锥得到的.
3：棱台的高和表面积
过棱台一个底面上的任意一个顶点，作另一个底面的垂线所得到的线段(或它的长度)称为棱台的高．
棱台所有侧面的面积之和称为棱台的侧面积．
4：正棱台及其性质
(1)正棱台的定义：由正棱锥截得的棱台称为正棱台．
(2)正棱台的性质：正棱台上、下底面都是正多边形，两者中心的连线是棱台的高；正棱台的侧面都全等，
且都是等腰梯形，这些等腰梯形的高也都相等，称为棱台的斜高．
概念辨析
1．判断正误
(1)用一个平面去截棱锥，底面和截面之间的部分叫棱台．( )
(2)棱台的侧面都是等腰梯形．( )
答案 (1)× (2)
2．下列命题中正确的是( )
A．棱台的侧面可以是平行四边形
B．两个底面平行且相似，其余各面都是梯形的多面体是棱台
C．棱台的底面是两个相似的正方形
D．棱台的侧棱延长后必交于一点
答案：D 棱台的侧面是梯形，一定不会是平行四边形，故A错；B中侧棱不一定交于一点；C中底面不一定是正方形．
例2.如图所示是一个正三棱台，而且下底面边长和侧棱长都为1，与分别是下底面和上底面的中心.
（1）求棱台的斜高；
（2）求棱台的高.
解：（1）因为是正三棱台，所以侧面都是全等的等腰梯形。
如图所示，在梯形中，分别过作AC的垂线与，则由
可知 ，从而 ，即斜高为.

（2）根据与分别为下底面和上底面的中心，以及下底面边长和上底面的边长分别为2，1,
可以算出：
假设正三棱台是由正棱锥截去正棱锥得到的，
则由已知可得
VO是棱锥的高，是棱锥的高，是所求棱锥的高.因此是一个直角三角形，画出这个三角形，
如图所示，则是的中位线.
因为棱台的棱长为1，所以，从而

因此： 因此棱台的高为：
通过对生活中实物的观察，引导学生观察、分析、抽象概括出棱锥与棱台的概念及基本结构。发展学生数学抽象和直观想象的核心素养。

通过观察、练习掌握棱锥与棱台的概念，掌握它们的相关计算问题，让学生经历抽象过程、发展学生数学抽象、数学运算、逻辑推理的核心素养。
通过观察与分析，获得棱台的相关概念，提高学生的数学抽象、数学建模及逻辑推理的核心素养。
通过观察分类、认识棱台模型，明确棱锥、棱台与棱柱的区别与联系。提高学生的数学抽象、数学建模及逻辑推理的核心素养。
三、达标检测
1．判断(正确的打“√”，错误的打“×”)
(1)有一个底面为多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体是棱锥． ( )
(2)棱台的侧棱长都相等．( )
(3)棱台的侧面展开图是由若干个等腰梯形组成的． ( )
[答案] (1)√ (2)× (3)×
2．在三棱锥A­BCD中，可以当作棱锥底面的三角形的个数为( )
A．1个 B．2个 C．3个 D．4个
D [在三棱锥A­BCD中，任何一个三角形都可作为棱锥的底面，所以有4个．]
3．如图，在三棱台A′B′C′­ABC中，截去三棱锥A′­ABC，则剩余部分是( )
A．三棱锥 B．四棱锥 C．三棱柱 D．三棱台
B [剩余几何体为四棱锥A′­BCC′B′.]
4．已知正四棱锥底面边长为6，侧棱长为5，则此棱锥的侧面积为________．
48 [正四棱锥的斜高h′＝eq \r(52－32)＝4，S侧＝4×eq \f(1,2)×6×4＝48.]
5．画一个三棱台，再把它分成：
(1)一个三棱柱和另一个多面体；
(2)三个三棱锥，并用字母表示．
[解] 画三棱台一定要利用三棱锥．
① ②
(1)如图①所示，三棱柱是棱柱A′B′C′­AB″C″，另一个多面体是C′B′BCC″B″.
(2)如图②所示，三个三棱锥分别是A′­ABC，B′­A′BC，C′­A′B′C.
6. 已知正三棱台的上、下底面边长分别为2和6，侧棱长为2eq \r(2)，求该三棱台的侧面积．
解：设正三棱台侧面梯形的高为h′，则h′＝ eq \r(2\r(2)2－\b\lc\(\rc\)(\a\vs4\al\c1(\f(6－2,2)))2)＝2.
∴S棱台侧＝3×eq \f(1,2)(d＋d′)h′＝3×eq \f(1,2)(2＋6)×2＝24.即该三棱台的侧面积为24.
通过练习巩固本节所学知识，通过学生解决问题，发展学生的数学直观、逻辑推理、数学建模和数学运算的核心素养。
四、小结
1．在理解的基础上，要牢记棱锥、棱台的定义，能够根据定义判断几何体的形状．
2．棱柱、棱台、棱锥关系图
五、课时练
通过总结，让学生进一步巩固本节所学内容，提高概括能力。