高中数学人教B版 (2019)必修 第四册11.3.1 平行直线与异面直线课时训练

11.3.1平行直线与异面直线

【基础练习】

一、单选题

1．空间两个角α，β的两边分别对应平行，且α=60°，则β为（　　）

A．60° B．120° C．30° D．60°或120°

【答案】D

【解析】

根据等角定理，两个角的两边分别对应平行，则两个角相等或互补，所以为或，故选D.

2．两个三角形不在同一平面内，它们的边两两对应平行，那么这两个三角形（    ）

A．全等 B．相似

C．仅有一个角相等 D．无法判断

【答案】B

【解析】

由题意知，根据等角定理，这两个三角形的三个角对应相等，

所以这两个三角形相似.

故选：B.

3．空间四边形ABCD的四条边所在直线成异面直线的有(　　)

A．1对 B．2对

C．3对 D．4对

【答案】B

【解析】　空间四边形ABCD的四条边所在直线中，成异面直线的有：AB和CD，AD和BC，

∴空间四边形ABCD的四条边所在直线成异面直线的有2对．

4．若、为异面直线，直线，则与的位置关系是（　　）

A．相交 B．异面 C．平行 D．异面或相交

【答案】D

【解析】

因为为异面直线，直线，则与的位置关系是异面或相交，选D

5．如图，在正方体中，，分别是，的中点，则下列直线中与直线互为异面直线的是(    )

A． B． C． D．

【答案】B

【解析】

对于A，直线与相交，所以两直线共面，故A不符合；

对于B，直线与既不平行也不相交，故B符合；

对于C，连接，则，且，

即四边形为平行四边形，所以，故两直线共面，C不符合；

对于D，直线与相交于点，故D不符合；

故选：B

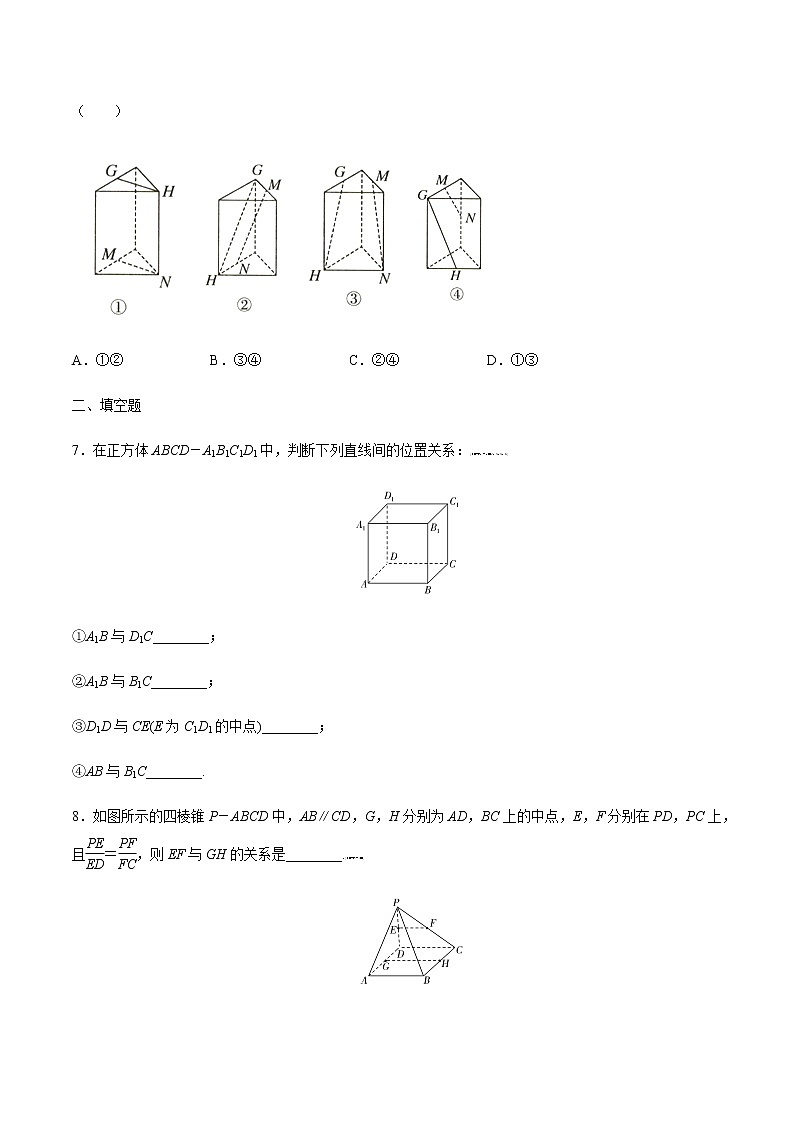
6．如图所示，若分别是三棱柱的顶点或所在棱的中点，则表示直线是异面直线的图形有（    ）

A．①② B．③④ C．②④ D．①③

【答案】C

【解析】

①中，，③中，连接，则且，故，必相交，②④符合题意.

故选C

二、填空题

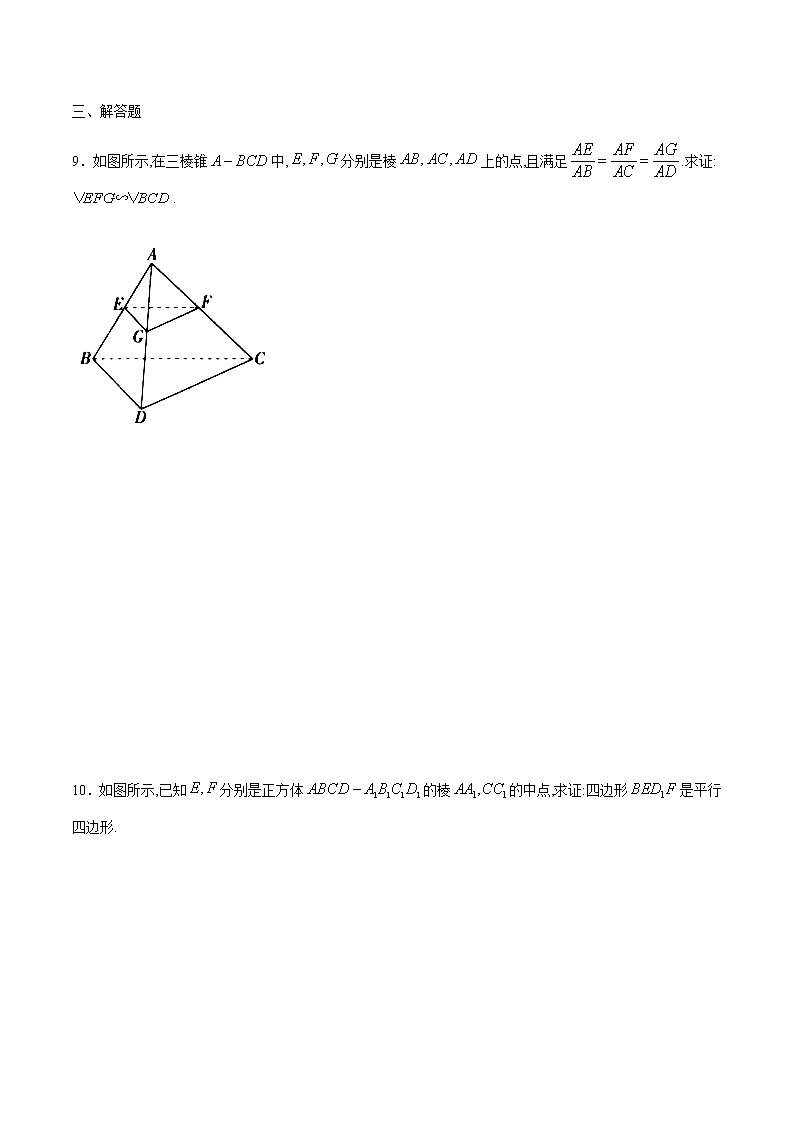
7．在正方体ABCD－A1B1C1D1中，判断下列直线间的位置关系：[来源:学。科。网Z。X。X。K]

①A1B与D1C________；

②A1B与B1C________；

③D1D与CE(E为C1D1的中点)________；

④AB与B1C________.

【答案】　①平行　②异面　③相交　④异面

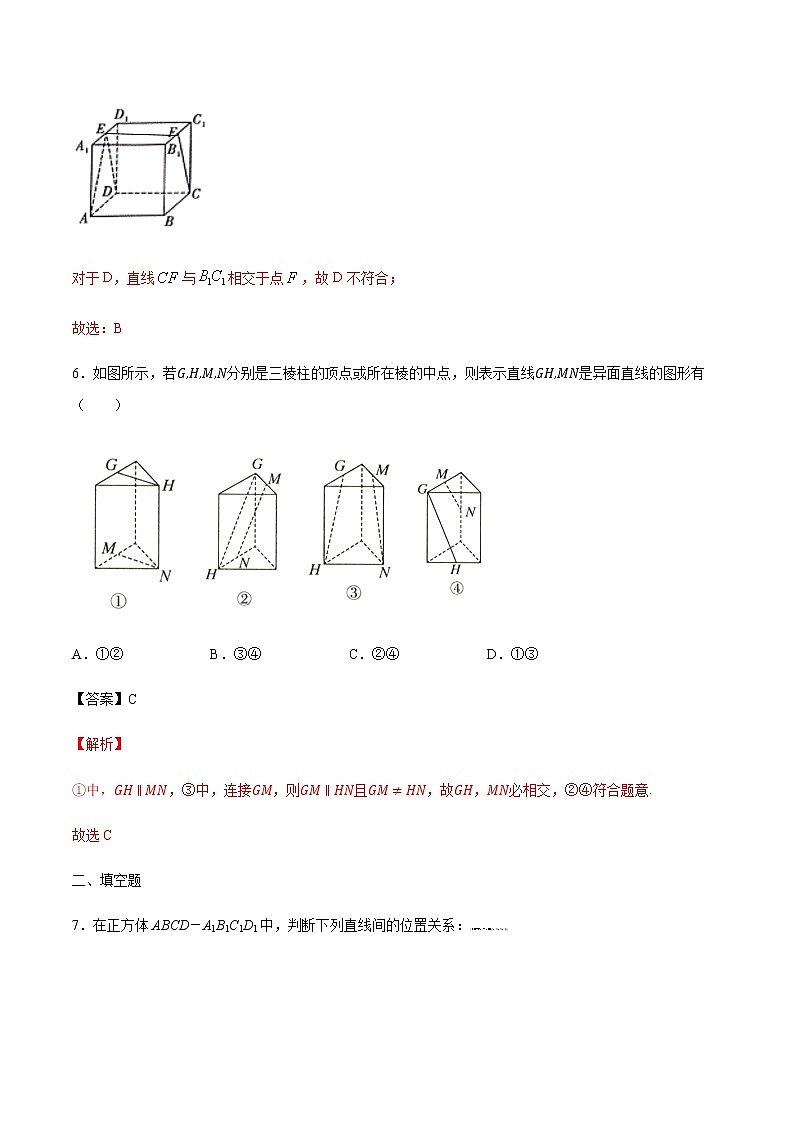
8．如图所示的四棱锥P－ABCD中，AB∥CD，G，H分别为AD，BC上的中点，E，F分别在PD，PC上，且＝，则EF与GH的关系是________.[来源:学+科+网]

【答案】平行　

【解析】∵AB∥CD，G，H分别为AD，BC的中点，∴GH∥DC，又∵在△PDC中，＝，∴EF∥DC，由平行线的传递性得，EF∥GH.

三、解答题

9．如图所示,在三棱锥中,分别是棱上的点,且满足.求证:.

【答案】见解析

【解析】

证明 在中,,

,且.

同理,,且.

又与的对应两边方向相同,

.

,

.

10．如图所示,已知分别是正方体的棱的中点,求证:四边形是平行四边形.

【答案】见解析

【解析】

证明 取的中点,连接.

∵是的中点,是的中点,.

由正方体的性质知,,

∴四边形是平行四边形,.

又分别是,的中点,

,且,

∴四边形为平行四边形,

,

,

∴四边形是平行四边形.

【提升练习】

一、单选题

1．已知是两两不同的三条直线，下列说法正确的是()

A．若直线异面，异面，则异面

B．若直线相交，异面，则相交

C．若，则与所成的角相等

D．若，则

【答案】C

【解析】

若直线异面，异面，则相交、平行或异面；若相交，相交，则相交、平行或异面；若，则相交、平行或异面；由异面直线所成的角的定义知C正确．

2．下列命题中，正确命题的个数是

①有三个公共点的两个平面重合  ②梯形的四个顶点在同一平面内

③三条互相平行的直线必共面    ④四条线段顺次首尾相接，构成平面图形

A．0 B．1 C．2 D．3

【答案】B

【解析】

详解：因为有三个不共线公共点的两个平面重合，所以①错；

因为梯形有两条直线相互平行，所以梯形的四个顶点在同一平面内，②对；

因为三条互相平行的直线不一定共面，如长方体三条平行的棱就不共面，所以③错，

因为四条线段顺次首尾相接可构成空间四边形，所以④错；

选B.

3．空间中有三条线段AB，BC，CD，且，那么直线AB与CD的位置关系是（  ）

A．平行 B．异面

C．相交或平行 D．平行或异面或相交均有可能

【答案】D

【解析】

解：

如图可知AB，CD有相交，平行，异面三种情况，故选D．

4．如图，在正方体中，M、N分别为棱C1D1、C1C的中点，有以下四个结论：

①直线AM与CC1是相交直线；    ②直线BN与MB1是异面直线；

③直线AM与BN是平行直线；        ④直线AM与DD1是异面直线．

其中正确的结论为（      ）

A．③④ B．①② C．①③ D．②④

【答案】D

【解析】

四点不共面，

直线与是异面直线，故①错误；

直线与不同在任何平面内，是异面直，故②正确；

直线与不同在任何平面内，是异面直线，故③错误；

直线与不同在任何平面内，是异面直，故④正确，故选D.

5．如图，G，H，M，N分别是正三棱柱的顶点或所在棱的中点，则表示GH，MN是异面直线的图形的序号为（    ）

A．①② B．③④ C．①③ D．②④

【答案】D

【解析】

如图所示：连接，易知，故是平行四边形，故，不异面，排除；

如图所示：连接，则，故四点共面，故共面，排除；

②④是异面直线.

故选：

二、填空题

6．已知，，是空间中的三条相互不重合的直线，给出下列说法：①若，，则；②若与相交，与相交，则与相交；③若平面，平面，则，一定是异面直线；④若，与成等角，则．其中正确的说法是______（填序号）．

【答案】①

【解析】

由公理4知①正确；

当与相交，与相交时，与可能相交、平行，也可能异面，故②不正确；

当平面，平面时，与可能平行、相交或异面，故③不正确；

当，与成等角时，与可能相交、平行，也可能异面，故④不正确．

故答案为：①

7.已知四边形ABCD是空间四边形，E、F、G、H分别是AB、BC、CD、DA的中点，则

(1)四边形EFGH是________；

(2)当AC＝BD时，四边形EFGH是________；

(3)当AC⊥BD时，四边形EFGH是________；[来源:学科网]

(4)当AC与BD满足________时，四边形EFGH是正方形．

【答案】　(1)平行四边形　(2)菱形　(3)矩形　(4)AC＝BD且AC⊥BD

三、解答题

8.   已知空间四边形ABCD中，AB≠AC，BD＝BC，AE是△ABC的边BC上的高，DF是△BCD的边BC上的中线，求证：AE与DF是异面直线.

【答案】详见解析

【解析】

首先说明、、三点均在面内，而不在面内，故而可得结论.

试题解析：由已知，得、不重合．

设所在平面为，则，，，，∴与异面．

9．如图，△ABC和△A′B′C′的对应顶点的连线AA′，BB′，CC′交于同一点O，且.

（1）求证：A′B′∥AB，A′C′∥AC，B′C′∥BC；

（2）求的值.

【答案】略

【解析】

（1）证明：∵AA′∩BB′＝O，且，∴AB∥A′B′，

同理，AC∥A′C′，BC∥B′C′.

（2）∵A′B′∥AB，A′C′∥AC且AB和A′B′、AC和A′C′方向相反，

∴∠BAC＝∠B′A′C′.同理．∠ABC＝∠A′B′C′，∠ACB＝∠A′C′B′，

∴△ABC∽△A′B′C′，∴，∴.

10．在三棱柱ABC－A1B1C1中，M，N，P分别为A1C1，AC和AB的中点．求证：∠PNA1＝∠BCM.

【答案】见解析

【解析】

因为，分别为，的中点，所以①，又因为分别为的中点，所以，所以四边形为平行四边形，于是②，由①②及与对应边方向相同，得.