高中数学人教B版 (2019)必修 第四册11.4.1 直线与平面垂直第1课时达标测试

11.4.1直线与平面垂直（1）

【基础练习】

一、单选题

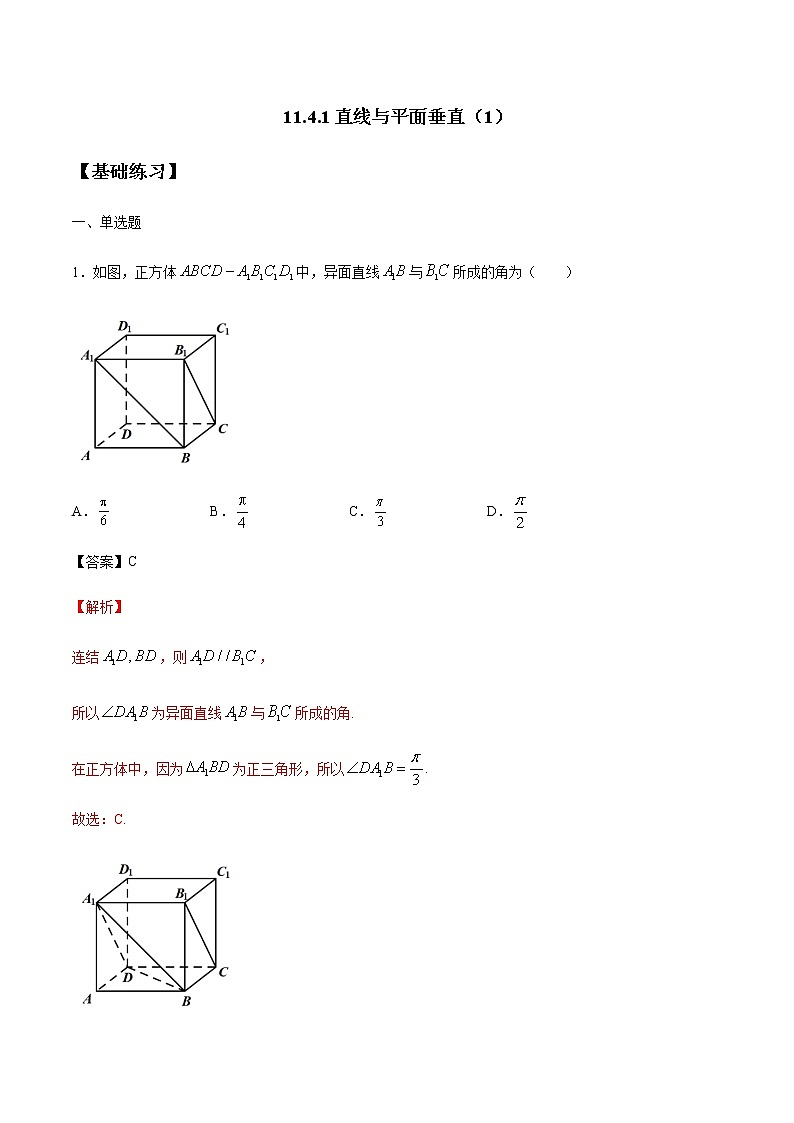
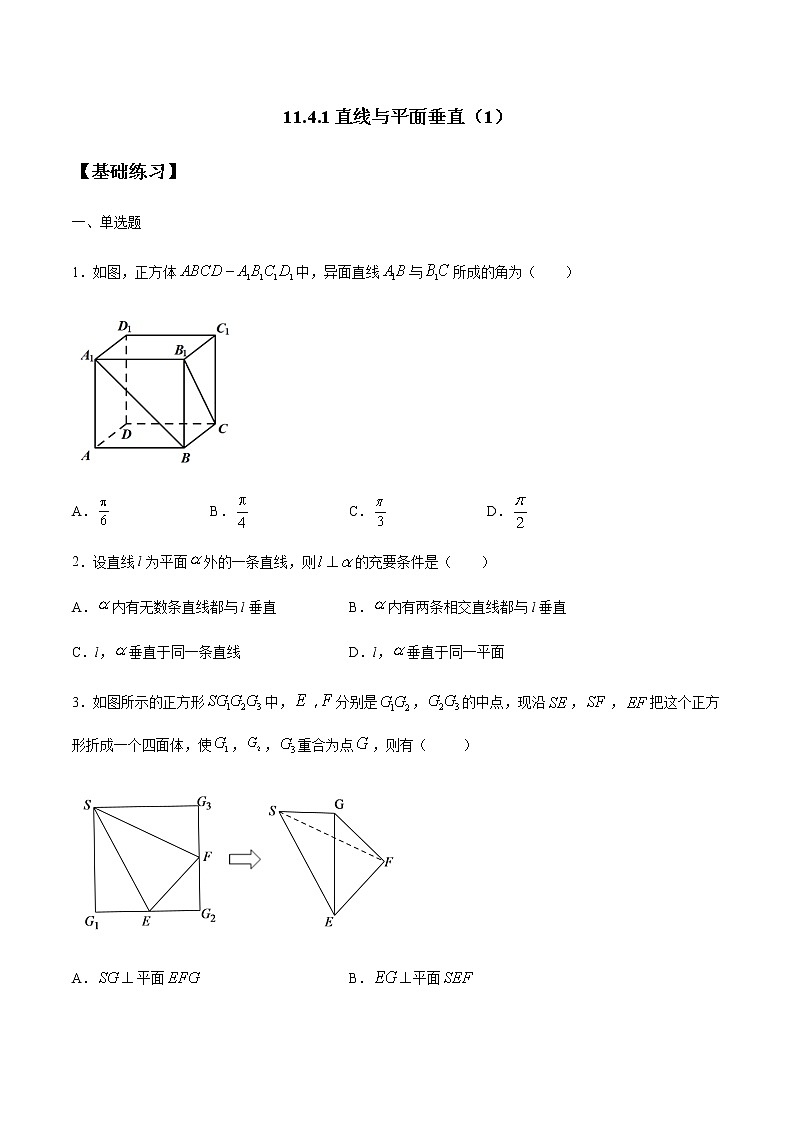
1．如图，正方体中，异面直线与所成的角为（    ）

A． B． C． D．

【答案】C

【解析】

连结，则，

所以为异面直线与所成的角.

在正方体中，因为为正三角形，所以.

故选：C.

2．设直线l为平面外的一条直线，则的充要条件是（    ）

A．内有无数条直线都与l垂直 B．内有两条相交直线都与l垂直

C．l，垂直于同一条直线 D．l，垂直于同一平面

【答案】B

【解析】

由线面垂直的判定定理知：

内两条相交直线都与l垂直是的充分条件；

由线面垂直的性质定理可知：

若，则内任意一条直线都与l垂直，

所以内两条相交直线都与l垂直是的必要条件

故选：B

3．如图所示的正方形中，分别是，的中点，现沿，，把这个正方形折成一个四面体，使，，重合为点，则有（     ）

A．平面 B．平面

C．平面 D．平面

【答案】A

【解析】

由题意：，，

，平面

所以平面正确，D不正确；.

又若平面，则，由平面图形可知显然不成立；

同理平面不正确；

故选：A

4．如图，ABCD﹣A1B1C1D1为正方体，则以下结论：①BD∥平面CB1D1；②AC1⊥BD；③AC1⊥平面CB1D1其中正确结论的个数是（　　　　）

A．0 B．1 C．2 D．3

【答案】D

【解析】

解：由正方体的性质得BD∥，所以结合线面平行的判定定理可得：BD∥平面；所以①正确.
由正方体的性质得 AC⊥BD，⊥BD，可得⊥平面 ，所以⊥BD，所以②正确.

　　　　
由正方体的性质得 BD∥，由②可得⊥BD，所以⊥，同理可得，进而结合线面垂直的判定定理得到：⊥平面 ，所以③正确.
故选：D.

5．如图，设平面，平面，平面，垂足分别为.为使，则需增加的一个条件是（    ）

A．平面 B．平面 C． D．

【答案】B

【解析】

因为平面，平面，

所以.

若平面，则由平面，得.

又与为相交直线，且平面，平面，则，

∴四点共面，

所以平面，

所以，

故选：B.

二、填空题

6．设，，为三条不同的直线，，为两个不同的平面，下列命题中正确的是______．

(1)若，，，则；

(2)若，，，则；

(3)若，，，，则；

(4)若，，,则．

【答案】(1)

【解析】

 (1) ， ，，则，正确

(2)若，，，则，错误

(3)若，则不成立，错误

(4)若，，,则，错误

7．四面体ABCD中，AB＝CD＝2，AC＝AD＝BC＝BD＝4，则异面直线AB与CD的夹角为_____．

【答案】

【解析】

如图所示：

取的中点，连接，

因为，为的中点，所以，

因为，为的中点，所以，

又，

所以平面，

因为平面，所以，

所以异面直线与所成的角为.

故答案为：

8．从正方体的个顶点中任意选择个点，记这个点确定的平面为，则垂直于直线的平面的个数为__________．

【答案】2.

【解析】

与直线垂直的平面有平面和平面，故与直线垂直的平面的个数为．

三、解答题

9．在长方体的面所在的平面中,分别写出与下列直线垂直的平面.

（1）;

（2）;

（3）.

【答案】（1）平面和平面.

（2）平面和平面.

（3）平面和平面.

【解析】

（1）根据线面垂直判定,即一条线垂直平面内的两条相交线,这条线垂直这个平面.

,,

面.

又 面面

面

（2）根据线面垂直判定,即一条线垂直平面内的两条相交线,这条线垂直这个平面.

,,

面

又 面面

面

（3）根据线面垂直判定,即一条线垂直平面内的两条相交线,这条线垂直这个平面.

,,

面

又 面面

面

10．四边形是圆柱的轴截面，为底面圆周上的一点，，，.

（1）求证：平面；

（2）求圆柱的表面积.

【答案】（1）见证明；（2）

【解析】

（1）证明：∵平面是圆柱的轴截面，

∴平面，∵平面，∴，

又为底面圆周上一点，为直径，∴，

又，∴平面

（2）在中

∵，，∴，

∴底面圆的半径，又∵

∴圆柱侧面积为，

上下两底面面积为，

∴圆柱的表面积为.

【提升练习】

一、单选题

1．如图，在圆锥SO中，AB，CD为底面圆的两条直径，AB∩CD＝O，且AB⊥CD，SO＝OB＝3，SE.，异面直线SC与OE所成角的正切值为（    ）

A． B． C． D．

【答案】D

【解析】

如图，过点S作SF∥OE，交AB于点F，连接CF，

则∠CSF（或补角）即为异面直线SC与OE所成的角，

∵，∴，

又OB＝3，∴，

SO⊥OC，SO＝OC＝3，∴；

SO⊥OF，SO＝3，OF＝1，∴；

OC⊥OF，OC＝3，OF＝1，∴，

∴等腰△SCF中，.

故选：D.

2．如图，在正方体的八个顶点中任取两个点作直线，与直线异面且夹角成的直线的条数为（    ）．

A． B． C． D．

【答案】B

【解析】

在正方体ABCD﹣A1B1C1D1的八个顶点中任取两个点作直线，

与直线A1B异面且夹角成60°的直线有：

AD1，AC，D1B1，B1C，共4条．

故选B．

3．如图，在正方形ABCD中，E、F分别是BC、CD的中点，G是EF的中点，现在沿AE、AF及EF把这个正方形折成一个空间图形，使B、C、D三点重合，重合后的点记为H，那么，在这个空间图形中必有（　　）

A．所在平面 B． 所在平面

C．所在平面 D．所在平面

【答案】B

【解析】

根据折叠前、后AH⊥HE，AH⊥HF不变，∴AH⊥平面EFH，B正确；

∵过A只有一条直线与平面EFH垂直，∴A不正确；

∵AG⊥EF，EF⊥AH，∴EF⊥平面HAG，∴平面HAG⊥AEF，过H作直线垂直于平面AEF，一定在平面HAG内，

∴C不正确；

∵HG不垂直于AG，∴HG⊥平面AEF不正确，D不正确．

故选B．

4．如图，在正方体中，是底面的中心，，为垂足，则与平面的位置关系是（    ）

A．垂直 B．平行 C．斜交 D．以上都不对

【答案】A

【解析】

连接.

∵几何体是正方体，底面是正方形，

∴.

又∵，∴平面.

∵平面，∴.

∵，∴平面.

故选A.

5．如图，四面体的棱平面，，则四面体的四个面中直角三角形的个数是（    ）

A．1 B．2 C．3 D．4

【答案】D

【解析】

∵四面体ABCD的棱平面ABC，，即为直角三角形，

∴，，即，为直角三角形

∴，

又∵，，

∴面，∴，即为直角三角形，

∴四面体的四个面中直角三角形共有4个，

故选：D.

二、填空题

6．如图，在直三棱柱中，底面是为直角的等腰直角三角形，，，是的中点，点在线段上，当_______时，平面.

【答案】或

【解析】

由已知得是等腰直角三角形，，是的中点，∴，

∵平面平面，平面平面，

∴平面，

又∵平面，∴.

若平面，则.

设，则，

，

∴，

解得或.

7．在正四棱锥中，底面正方形的边长为1，侧棱长为2，则异面直线与所成角的大小为__________．

【答案】

【解析】

如图所示，连接AC，交BD于O，连接VO

∵四边形ABCD是正方形，

∴AC⊥BD，O为BD的中点

又∵正四棱锥V﹣ABCD中，VB＝VD

∴VO⊥BD

∵AC∩VO＝O，AC、VO⊂平面ACV

∴BD⊥平面ACV

∵VA⊂平面ACV

∴BD⊥VA；

即异面直线VA与BD所成角等于．．

故答案为．

8．如图所示，在四棱锥中，垂直于正方形所在的平面，在这个四棱锥的所有表面及面、面中，一定互相垂直的平面有_________对．

【答案】7

【解析】

由PD⊥面ABCD，则面PDA⊥面ABCD、面PDB⊥面ABCD、面PDC⊥面ABCD；由AD⊥CD，AD⊥PD，PD∩CD=D，则AD⊥面PDC，所以面PAD⊥面PDC；同理可证AB⊥面PDA，BC⊥面PDC，AC⊥面PDB，从而有：面PAB⊥面PDA、面PBC⊥面PDC、面PAC⊥面PDB，综上，互相垂直的平面有7对.

所以本题答案为7.

三、解答题

9．如图所示，在长方体中，， 为棱上—点.

(1)    若，求异面直线和所成角的大小；

(2)    若，求证平面.

【答案】(1) ；(2)证明详见解析.

【解析】

 (1),

是异面直线和所成角,

∵在长方体中,平面,

,

,,,M为棱上一点,,

,

,

即异面直线和所成角的大小为.

(2) 时,,

,.

,,

,

,

又,平面.

10．如图，长方体ABCD﹣A1B1C1D1中，AB＝BC＝4，BB1＝2，点E、F、M分别为C1D1，A1D1，B1C1的中点，过点M的平面α与平面DEF平行，且与长方体的面相交，交线围成一个几何图形．

（1）在图1中，画出这个几何图形，并求这个几何图形的面积（不必说明画法与理由）

（2）在图2中，求证：D1B⊥平面DEF．

【答案】（1）6（2）见解析

【解析】

（1）设N为A1B1的中点，连结MN，AN、AC、CM，

则四边形MNAC为所作图形．

由题意知MN∥A1C1（或∥EF），四边形MNAC为梯形，

且MNAC＝2，

过M作MP⊥AC于点P，

可得MC2，PC，

得MP，

∴梯形MNAC的面积（24）6．

证明：（2）示例一：在长方体中ABCD﹣A1B1C1D1，

设D1B1交EF于Q，连接DQ，

则Q为EF的中点并且为D1B1的四等点，如图，

D1Q4，

由DE＝DF得DQ⊥EF，又EF⊥BB1，

∴EF⊥平面BB1D1D，∴EF⊥D1B，

，∴∠D1QD＝∠BD1D，

∴∠QD1B+∠D1QD＝∠DD1B+∠BD1Q＝90°，

∴DQ⊥D1B，∴D1B⊥平面DEF．

示例二：设D1B1交EF于Q，连接DQ，则Q为EF的中点，

且为D1B1的四等分点，D1Q4，

由BB1⊥平面A1B1C1D1可知BB1⊥EF，

又B1D1⊥EF，BB1∩B1D1＝B1，∴EF⊥平面BB1D1D，∴EF⊥D1B，

由，得tan∠QDD1＝tan∠D1BD，

得∠QDD1＝∠D1BD，∴∠QDB+∠D1BD＝∠QDB+∠QDD1＝90°，

∴DQ⊥D1B，又DQ∩EF＝Q，∴D1B⊥平面DEF．

；